Логарифмические частотные характеристики
В инженерной практике часто пользуются логарифмическими эквивалентами АЧХ и ФЧХ: логарифмической амплитудно-частотной характеристикой (ЛАЧХ)
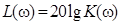 (1.12)
(1.12)
и логарифмической фазово-частотной характеристикой (ЛФЧХ)
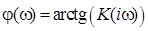 . (1.13)
. (1.13)
По оси абсцисс значения w (или f – Гц) откладываются в логарифмическом масштабе. Основные деления сетки частоты отличаются на декаду (в 10 раз). При этом обычно пересечение осью ординат оси абсцисс выбирают в значении 1 рад/с (1Гц).
В отличие от АЧХ, имеющей линейный масштаб изменения коэффициента передачи, изменение ординаты ЛАЧХ линейно по отношению к приращению функции в дБ.
По оси ординат графиков ФЧХ и ЛФЧХ фаза откладывается в градусах либо в радианах. Масштаб линейный. Отличие их в масштабе по оси абсцисс. В первом случае он линейный, во втором – логарифмический. Таким образом, и ЛЧХ, и ЛФЧХ – полулогарифмические характеристики.
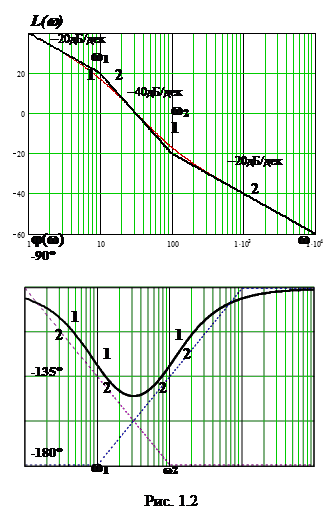 На рисунке 1.2 (графики 1) приведены графики ЛАЧХ и ЛФЧХ для ЧПФ
На рисунке 1.2 (графики 1) приведены графики ЛАЧХ и ЛФЧХ для ЧПФ 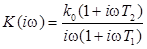 при k0 = 100 (40 дБ), Т1 = 0,1 с, Т2 = 0,01 с
при k0 = 100 (40 дБ), Т1 = 0,1 с, Т2 = 0,01 с
Экспериментально ЛАЧХ и ЛФЧХ исследуются в установившемся режиме. При этом на вход звена или системы подают гармоническое воздействие с постоянной амплитудой x(t)=X0sin(w t), частота w изменяется либо дискретно, либо непрерывно, например, по линейному закону. В последнем случае изменения частоты должны быть медленнее наибольшей постоянной времени РАС.
|
Асимптотические ЛАЧХ и ЛФЧХ.В инженерной практике применяют приближенные эквиваленты ЛАЧХ и ЛФЧХ – асимптотические логарифмические частотные характеристики.
Для построения асимптотической ЛАЧХ динамического звена прежде всего следует выяснить тип звена, определить пределы изменения частоты, коэффициент передачи на постоянном токе и частоты сопряжения.
Пределы изменения частоты w достаточно ограничить интервалом
fmin/30 = 1/30Тmax ... 30 fmax = 30/Tmin , (1.14)
где Тmin и Тmax – соответственно, наибольшее и наименьшее значения постоянных времени звена.
Частоты сопряжения находят через постоянные времени звена (wj = 1/Тj). ЧПФ необходимо свести к виду (1.15), для этого числитель и знаменатель представляют в виде произведения множителей вида (1 + iwТj).
Если такой множитель будет в знаменателе, его асимптотическая ЛАЧХ до частоты сопряжения wj имеет постоянную асимптоту ЛАЧХ 0 дБ, после wj асимптота линейно убывает со скоростью – 20 дБ/дек (дБ на декаду или – 6 дБ на октаву); а ЛФЧХ до частоты сопряжения wj будет примерно равна 0°, после
wj – примерно – 90°, на частоте wj = – 45°.
Если множитель (1 + iwТj) окажется в числителе, его асимптотическая ЛАЧХ до частоты сопряжения wj будет постоянной на уровне 0 дБ. После wj асимптота линейно будет возрастать со скоростью + 20 дБ/дек, а ЛФЧХ до частоты сопряжения wj будет примерно равна 0°, после wj – примерно + 90°, на частоте wj = + 45°.
На рисунке 1.2 (графики 2) построены асимптотические ЛАЧХ и ЛФЧХ. Для их построения необходимо найти частоты сопряжения w1 = 1/Т1 = 10 рад/с,
w2 = 1/Т2 = 100 рад/с.
Звено в числителе (форсирующее – классификацию звеньев см. в п. 2.4, а также прил. 2) до частоты w2 имеет постоянную асимптоту ЛАЧХ 0 дБ, а после нее асимптота линейно возрастает со скоростью + 20 дБ/дек.
Звенья в знаменателе: первое (идеальный интегратор) дает асимптоту ЛАЧХ, которая начинается на уровне + 40 дБ (k0) при w = 1 и убывает со скоростью – 20 дБ/дек; второе (апериодическое) до частоты w1 имеет постоянную асимптоту ЛАЧХ 0 дБ, а после нее асимптота линейно убывает со скоростью –20 дБ/дек.
После суммирования асимптотических ЛАЧХ звеньев получим итоговую асимптотическую ЛАЧХ (рис. 1.2 график 2).
Максимальная погрешность асимптотической ЛАЧХ получается на частотах сопряжения и не превышает 3 дБ.
Для минимально фазовых цепей достаточна грубая оценка ЛФЧХ. Итоговая асимптотическая ЛФЧХ (рис. 1.2 график 2) получается суммированием ЛФЧХ звеньев: интегрирующее звено имеет постоянный фазовый сдвиг – 90°, фаза звена первого порядка изменяется с ростом w от 0 до – 90° (апериодическое) или от 0 до + 90° (форсирующее), проходя на частотах сопряжения через значение ± 45°.
Динамическое звено – элемент системы, обладающий свойствами однонаправленности и независимости. Число динамических звеньев структурной схемы определяется удобством математического описания РАС.
На практике ПФ РАС представляет собой произведение передаточных функций динамических звеньев, порядок полинома ПФ которых не выше второго.
K(p)= 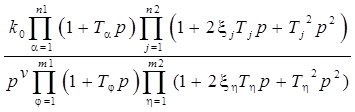 , (1.15)
, (1.15)
где Т – постоянная времени звена, с; z – коэффициент демпфирования (обратная величина добротности) системы; v – количество интеграторов (показатель астатизма системы). В числителе (1.15) собираются множители с опережением по фазе, в знаменателе (1.15) – с отставанием по фазе.
Динамические звенья разделяют на интегрирующие, дифференцирующие и позиционные звенья. Характеристики элементарных звеньев (схема, ПФ, ПХ, ИХ) приведены в приложении 2.
К позиционным звеньям относятся
· звенья пропорционального регулирования (ПФ 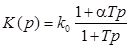 );
);
· апериодические (ПФ 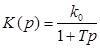 , w < wс1);
, w < wс1);
· колебательные (ПФ 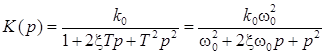 );
);
· безынерционные (ПФ K(p) = k0).
К интегрирующим звеньям относятся
· идеальные интеграторы (ПФ 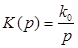 );
);
· инерционные интеграторы (ПФ 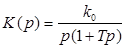 );
);
· замедляющие (апериодические) (ПФ 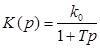 , w > wс1) и
, w > wс1) и
· изодромные (ПФ 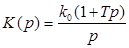 ) звенья.
) звенья.
К дифференцирующим звеньям относятся
· идеально дифференцирующие (K(p) = k0p);
· дифференцирующие с замедлением (ПФ 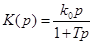 ) и
) и
· форсирующие звенья (ПФ K(p) = k0(1+Tp)) .
Для звена с чистым запаздыванием на время t: K(p) = e–pτ « f(t–τ) .
Задание № 1. Исследование простейших
динамических звеньев
Исходные данные задания для различных вариантов приведены в табли- це 1.2, а соответствующие схемы – в таблице 1.3.
1. Для заданной схемы и номиналов ее элементов получить ПФ [1].
2. Найти аналитические выражения и построить графики АЧХ, ФЧХ, ЛАЧХ, ЛФЧХ (в том числе асимптотических).
3. Построить годограф цепи.
4. Получить аналитические выражения и построить графики ИХ и ПХ.
5. Указать требования к испытательным сигналам для экспериментального исследования АЧХ, ФЧХ, ИХ и ПХ.
|
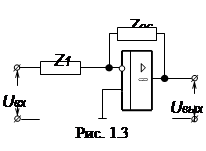
Таблица 1.2
| Вариант | ||||||||||
| № схемы | ||||||||||
| R1, кОм | 0,051 | 0,068 | 3,3 | 0,1 | 5,1 | 0,2 | ||||
| C1, мкФ | – | 0,1 | 0,5 | 0,033 | 0,1 | – | 0,33 | 0,5 | – | |
| R2, кОм | 5,1 | – | 8,2 | – | – | |||||
| C2, мкФ | – | – | – | 2,2 | – | 3,3 | – | – | ||
| L1, мГн | – | – | – | – | – | – | ||||
| L2, мГн | – | – | – | – | – | – | – | – |
| Вариант | ||||||||||
| № схемы | ||||||||||
| R1, кОм | 3,3 | 5,1 | 6,8 | 4,7 | 0,1 | 5,1 | 7,5 | |||
| C1, мкФ | 0,5 | 0,5 | 0,25 | – | 0,05 | 0,33 | ||||
| R2, кОм | 8,2 | 7,5 | 3,3 | |||||||
| C2, мкФ | – | – | – | – | – | – | – | 0,1 | – | |
| L1, мГн | – | – | – | – | – | – | – | – | – | |
| R3, кОм | – | – | – | – | – | – |
| Вариант | ||||||||||
| № схемы | ||||||||||
| R1, кОм | 7,5 | 8,2 | 3,3 | 0,15 | 3,3 | |||||
| C1, мкФ | 0,01 | 0,25 | 0,1 | 0,1 | 0,5 | 0,33 | 0,2 | |||
| R2, кОм | 8,2 | |||||||||
| C2, мкФ | 0,5 | – | 0,5 | – | – | – | – | – | – | |
| L1, мГн | – | – | – | – | – | – | – | – | – |
| Вариант | ||||||||||
| № схемы | ||||||||||
| R1, кОм | 7,5 | 0,22 | 0,1 | |||||||
| C1, мкФ | 0,5 | – | 3,3 | 0,1 | 0,33 | 0,5 | 0,2 | |||
| R2, кОм | – | 5,1 | – | 3,3 | ||||||
| C2, мкФ | 2,2 | – | – | – | 0,5 | – | – | |||
| L1, мГн | – | – | – | – | – | – | – | – |
| Вариант | ||||||||||
| № схемы | ||||||||||
| R1, кОм | 3,3 | 5,1 | 6,8 | 4,7 | 0,1 | 5,1 | 7,5 | |||
| C1, мкФ | 0,5 | 0,5 | 0,25 | – | 0,05 | 0,33 | ||||
| R2, кОм | 8,2 | 7,5 | 3,3 | |||||||
| C2, мкФ | – | – | – | – | – | – | – | 0,1 | – | |
| L1, мГн | – | – | – | – | – | – | – | – | – | |
| R3, кОм | – | – | – | – | – | – |
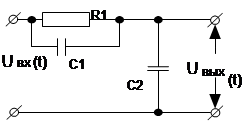
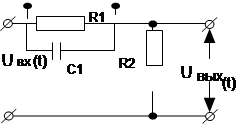
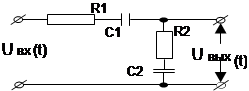
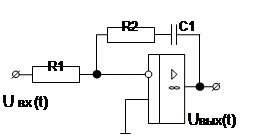
Таблица 1.3
| Вари-ант | Схема | Вари-ант | Схема |
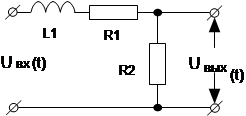 | 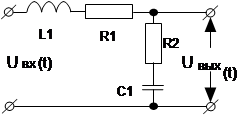 | ||
 |  | ||
 | 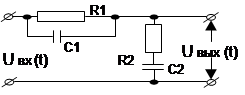 | ||
 | 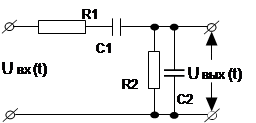 | ||
 |  |
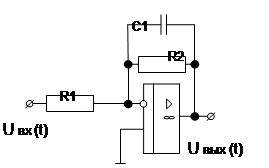
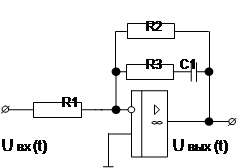
Окончание табл. 1.3
| Вари-ант | Схема | Вари-ант | Схема |
 |  | ||
 | 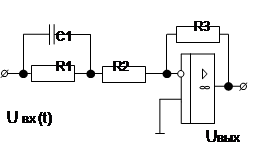 | ||
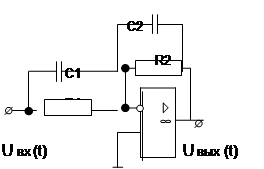 | 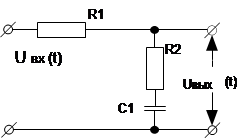 |

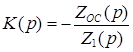 . (1.16)
. (1.16)