Понятие случайных функций
III. Случайные функции.
Основы корреляционного анализа
Понятие случайных функций
Понятие случайной функции возникло в результате наблюдения многочисленных явлений и процессов в природе, технике, экономике. Изменения во времени и пространстве температуры воздуха, давления и других метеоэлементов; флуктуации напряжения и силы тока в электрической цепи; колебания спроса на те или иные виды товаров — эти и многие другие примеры показывают необходимость создания математического аппарата анализа наблюдений за количественными характеристиками подобных явлений и процессов.
Случайной функцией (или случайным процессом) обычно называют случайную величину, зависящую от детерминированного параметра. Этим параметром может быть время, частота, расстояние, направление и т. п., но традиционно принято вести изложение, используя в качестве такого параметра время. Общая теория стационарных случайных процессов была создана в основном в 30-е годы XX века.
Математическая теория анализа случайных величин, зависящих от детерминированного параметра, называется теорией случайных функций (случайных процессов). Остановимся на некоторых основных понятиях теории случайных функций.
Для записи случайного процесса примем обозначение Y (t),где параметр t (время) принадлежит некоторому вещественному конечному или бесконечному интервалу (a, b). Любой фиксированной точке t1этого интервала соответствует случайная величина Y(t1).
В результате наблюдения выявляется реализация или выборочная функция процесса Y(t).Реализация yi(t), полученная в результате i-го наблюдения,является детерминированной функцией времени t, она принимает тот или иной конкретный вид.Несколько выборочных функций образуют ансамбль реализаций. При проведении экспериментов выявляется одна реализация (или ансамбль реализаций) из бесконечного множества выборочных функций {y(t)},называемого выборочным пространством. Таким образом, случайную функцию можно рассматривать как совокупность всех ее реализаций.
Значения реализаций, определенные при заданном значении аргумента, т.е. y1(t0), y2(t0),…,yn(t0), представляют собой случайные величины и называются сечением случайной функции.
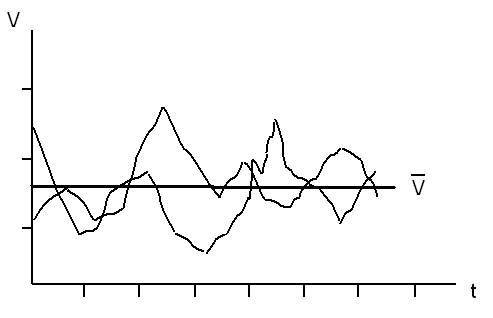
Рис.1. Турбулентные пульсации скорости ветра
Если аргумент случайной функции принимает определенные дискретные значения, случайную функцию называют случайной последовательностью.
Случайный процесс дает вероятностное описание физического явления, которое развивается во времени по вполне определённым вероятностным законам. Он сочетает в себе черты детерминированной функции и случайной величины: при t= const он превращается в случайную величину, а при фиксированном номере опыта (i = const) — в детерминированную функцию.
Если число реализаций случайного процесса бесконечно велико, то такой процесс называют ансамблем. Чем больше число факторов влияют на эксперимент, тем шире становится ансамбль и, следовательно, тем большая осторожность нужна при интерпретации результатов, полученных по нему. Поэтому вопрос о том, какие реализации являются наиболее представительными для данного ансамбля, должен решаться на основе дополнительных априорных сведений о характере случайного процесса, а не на основе чисто статистических заключений.
Понятие случайной функции является слишком широким и общим, и при исследовании обычно ограничиваются определенными классами и типами процессов, являющихся абстрактными аналогами реальных физических процессов.
Поскольку случайный процесс есть случайная величина, зависящая от параметра, то от этого параметра будут зависеть и моментные характеристики. В качестве первой такой характеристики определим математическое ожидание или среднее значение
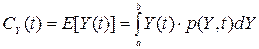 , (1)
, (1)
где p(Y,t) – плотность вероятности. Математическое ожидание С(t)представляет собой детерминированную функцию времени. Отдельные реализации флуктуируют около С(t)и в каком-то смысле близки к ней.
Следующей характеристикой случайного процесса, дающей описание вторых моментов, является ковариационная функция, определяемая равенством
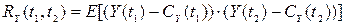 , (2)
, (2)
где RY(t1, t2) есть детерминированная функция двух переменных t1 и t2 показывающая, какова статистическая зависимость случайных величин Y(t1) и Y(t2). При t1 = t2 = t из (2) имеем
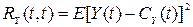 . (3)
. (3)
Функция 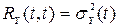 называется дисперсией случайного процесса Y(t). Дисперсия характеризует разброс отдельных реализаций относительно математического ожидания для каждого значения
называется дисперсией случайного процесса Y(t). Дисперсия характеризует разброс отдельных реализаций относительно математического ожидания для каждого значения 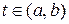 .
.
