Координатные плоскости Oxa и Oax
Функционально-графические методы
Встречающиеся задачи на исследование уравнения или неравенства с параметром аможно записать в виде 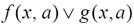 , где символ
, где символ 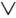 заменяет один из знаков =, > , < ,
заменяет один из знаков =, > , < , 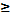 ,
, 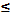 . Так как основу уравнений и неравенств составляют выражения f(x,а)и g(x,a), то в зависимости от того, какая роль отводится параметру в задаче (параметр – фиксированное число, или параметр – переменная), запись f(x,a) рассматривается либо как семейство функций с переменной x , либо как выражение с двумя переменными xи а. В соответствии с этим используется два основных графических приема решения подобных задач: первый – построение графического образа задачи на координатной плоскости Oxy, второй – на координатных плоскостях Oxaили Oax.
. Так как основу уравнений и неравенств составляют выражения f(x,а)и g(x,a), то в зависимости от того, какая роль отводится параметру в задаче (параметр – фиксированное число, или параметр – переменная), запись f(x,a) рассматривается либо как семейство функций с переменной x , либо как выражение с двумя переменными xи а. В соответствии с этим используется два основных графических приема решения подобных задач: первый – построение графического образа задачи на координатной плоскости Oxy, второй – на координатных плоскостях Oxaили Oax.
§1 Координатная плоскость Oxy
задачи вида 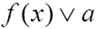
При решении задач данного вида на координатной плоскости Oxy изображают график функции f(x)= y.Тогда при заданном значении параметра aмножество решений уравнения f(x)= aявляется проекцией на ось абсцисс точек пересечения горизонтальной прямой y=a с графиком функции f(x),амножество решений неравенства 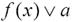 является проекцией на ось абсцисс всех точек прямой y=a, ординаты которых удовлетворяют неравенству
является проекцией на ось абсцисс всех точек прямой y=a, ординаты которых удовлетворяют неравенству 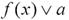 .
.
Возможны ситуации:
1. Прямая 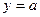 не пересекает график
не пересекает график 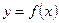 . Следовательно, при данном значении а исходное уравнение решений не имеет.
. Следовательно, при данном значении а исходное уравнение решений не имеет.
2. Прямая 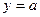 пересекает график
пересекает график 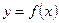 в одной или нескольких точках. Следовательно, при данном значении а можно сделать вывод о числе решений исходного уравнения, найти абсциссы точек пересечения и т.д.
в одной или нескольких точках. Следовательно, при данном значении а можно сделать вывод о числе решений исходного уравнения, найти абсциссы точек пересечения и т.д.
Пример 1: Определите количество
различных корней уравнения
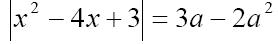
в зависимости от параметра а.
Решение:
Рассмотрим взаимное расположение графика функии 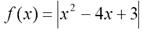 и прямой
и прямой 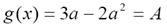 на координатной плоскости Оху. Из рисунка 1 видно, что при А < 0 графики не имеют общих точек; если 0<A<1, то графики имеют четыре точки пересечения; две общие точки получаем при условии А= 0 или А>1.
на координатной плоскости Оху. Из рисунка 1 видно, что при А < 0 графики не имеют общих точек; если 0<A<1, то графики имеют четыре точки пересечения; две общие точки получаем при условии А= 0 или А>1.
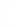
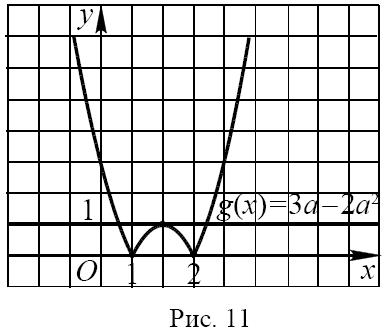
На рисунке 1 представлен случай, когда графики имеют ровно три общих точки. Данное уравнение имеет три различных корня, если выполняется условие 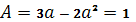 . Отсюда а = 0,5 или а = 1. Аналогично находим а для других случаев.
. Отсюда а = 0,5 или а = 1. Аналогично находим а для других случаев.
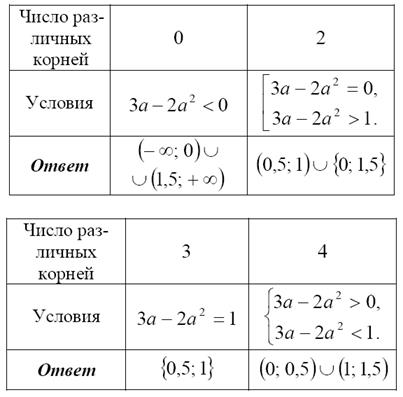
Пример 2: Найти число решений уравнения 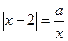 .
.
Решение
Заметим, что х не равно нулю. Умножим обе части уравнения на 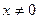 . Получим
. Получим 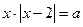
Построим график функции 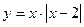 .
.
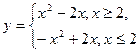
 Графиком функции
Графиком функции 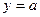 является прямая, параллельная оси ОХ.
является прямая, параллельная оси ОХ.
Анализируя графическую иллюстрацию, понятно, что при а=0 одно решение, т.к. одна точка пересечения (не забываем, что х не равен нулю). При а=1 две точки пересечения графика функции и прямой, а значит и два решения. При а<0 получается одна точка пересечения, как и при а>1. Если же 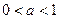 , то график функции и прямая имеют три точки пересечения.
, то график функции и прямая имеют три точки пересечения.
Ответ:при 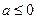 ,
, 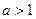 одно решение,
одно решение,
Координатные плоскости Oxa и Oax
Данный метод представляет собой некоторое обобщение графического метода решения уравнений и неравенств, основанного на использовании координатной плоскости Oxa или Oax . В последнем случае ось Ox называют координатной, ось Oa – параметрической, а плоскости Oxa и Oax – координатно-параметрическими (или КП – плоскостями).
Пример 3: При каких значениях параметра а имеет ровно два различных корня уравнения.
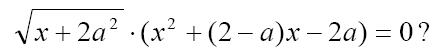
Решение
Корни данного уравнения должны удовлетворять условию 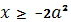 (условия существования квадратного коря из выражения
(условия существования квадратного коря из выражения 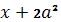 ). Заметим, что
). Заметим, что 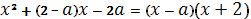 . Тогда
. Тогда
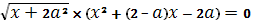
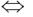
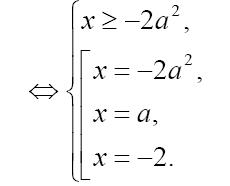
Следовательно, корнями уравнения могут быть числа 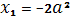 ,
, 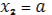 и
и 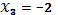 . По условию задачи требуется найти значение параметра а, при которых уравнение имеет ровно два различных корня. Для отбора искомых значений параметра на плоскости Oax построим графики функций
. По условию задачи требуется найти значение параметра а, при которых уравнение имеет ровно два различных корня. Для отбора искомых значений параметра на плоскости Oax построим графики функций 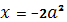 ,
, 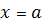 и
и 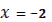 (см. рис.2). Каждая прямая при a = const параллельна оси Ox и пересекает каждый из построенных графиков, и ордината точки пересечения дает значения корня исходного уравнения при условии, что
(см. рис.2). Каждая прямая при a = const параллельна оси Ox и пересекает каждый из построенных графиков, и ордината точки пересечения дает значения корня исходного уравнения при условии, что 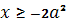 . Точки (a, x),координаты которых удовлетворяют последнему неравенству, расположены на плоскости Oax в выделенной фоном области.
. Точки (a, x),координаты которых удовлетворяют последнему неравенству, расположены на плоскости Oax в выделенной фоном области.
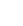
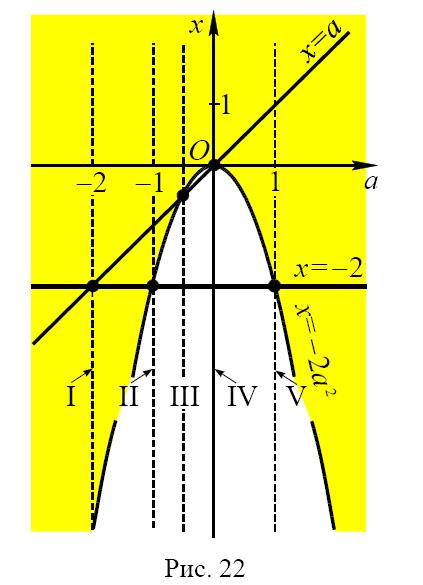
Имеется пять критических положений этих прямых:
1) 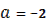 , 2)
, 2) 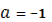 , 3)
, 3) 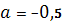 , 4)
, 4) 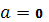 , 5)
, 5) 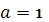 .
.
В этих случаях они проходят через точки пересечения графиков. Точки – 2, - 1, - 0,5, 0 и 1 разбивают числовую прямую Oa на шесть промежутков. Рассмотрим каждый из них:
(1) 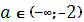 и (2)
и (2) 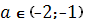 . На этих промежутках уравнение имеет три корня.
. На этих промежутках уравнение имеет три корня.
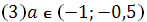 . Уравнение имеет два корня ( график функции
. Уравнение имеет два корня ( график функции 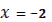 расположен ниже графика функии
расположен ниже графика функии 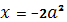 ).
).
(4) 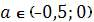 . Уравнение имеет один корень, так как графики функций
. Уравнение имеет один корень, так как графики функций 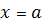 и
и 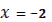 – ниже графика функции
– ниже графика функции 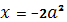 .
.
(5) 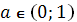 .Уравнение имеет два корня ( график функции
.Уравнение имеет два корня ( график функции 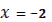 - ниже графика функции
- ниже графика функции 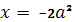 ).
).
(9) 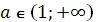 . Уравнение имеет три корня.
. Уравнение имеет три корня.
Соответственно при каждом из значений 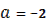 ,
, 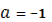 или
или 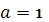 уравнение имеет два корня.
уравнение имеет два корня.
Ответ: 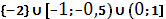 .
.
Пример 4: Определить значение параметра a, при которых уравнение 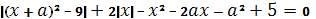 будет иметь наибольшее число корней.
будет иметь наибольшее число корней.
Решение
Приведем уравнение к следующему виду 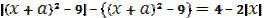 . (*)
. (*)
Рассмотрим два случая.
1) Если 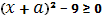 , то уравнение будет иметь вид . Отсюда
, то уравнение будет иметь вид . Отсюда 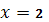 и
и 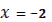 . Для того, чтобы найденные значения
. Для того, чтобы найденные значения 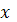 являлись решениями уравнения (*), должны выполняться условия:
являлись решениями уравнения (*), должны выполняться условия:
Если 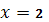 , то
, то 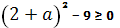
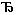
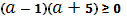
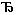
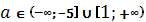 ;
;
Если 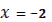 , то
, то 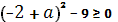
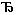
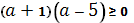
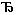
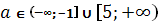 .
.
2) Если 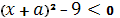 , то уравнение будет иметь вид
, то уравнение будет иметь вид 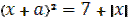 .
.
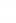
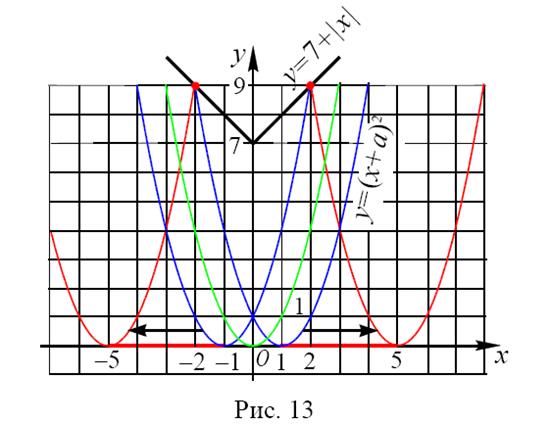
На рис.3 представлены графики функций 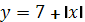 , стоящей в правой части последнего уравнения, и графики функций
, стоящей в правой части последнего уравнения, и графики функций 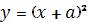 ,стоящей в левой его части а. Так как должно выполняться условие
,стоящей в левой его части а. Так как должно выполняться условие 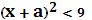 , то для существования корней должно быть и
, то для существования корней должно быть и 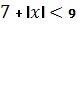 , т.е
, т.е
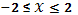 . Это возможно только при
. Это возможно только при 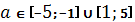 (см.рис.3)
(см.рис.3)
Причем решение при этих значениях aбудет одно. При 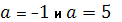 получается
получается 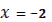 ; при
; при 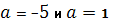 получим
получим 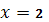 ; при
; при 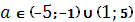 решением будет некоторое
решением будет некоторое 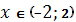 .
.
Сравнивая полученные решения в первом и втором случаях, имеем: при 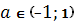 уравнение не имеет решений; при
уравнение не имеет решений; при 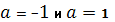 уравнение имеет одно решение; при
уравнение имеет одно решение; при 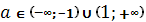 уравнение имеет два решения.
уравнение имеет два решения.
Ответ: При 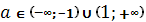 уравнение имеет два корня.
уравнение имеет два корня.
Пример 5: Найдите все значения а, при каждом из которых уравнение 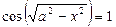 имеет ровно восемь различных решений.
имеет ровно восемь различных решений.
Решение:
1 способ. 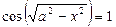 ,
, 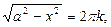
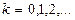
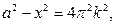
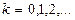
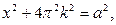
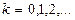
Построим графики функций 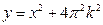 при
при 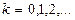 и
и 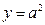 . Графиком первой функции является семейство парабол с вершинами, расположенных на оси ОУ: у=0,
. Графиком первой функции является семейство парабол с вершинами, расположенных на оси ОУ: у=0, 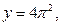
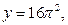
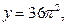
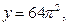
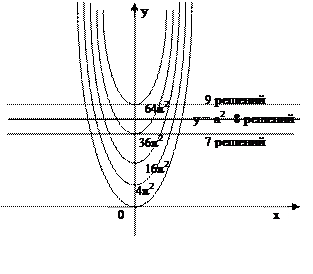 и т.д. (в зависимости от k=0,1,2,3,4,…). Графиком второй функции является прямая, параллельная оси ОХ.
и т.д. (в зависимости от k=0,1,2,3,4,…). Графиком второй функции является прямая, параллельная оси ОХ.
По графику определяем, что
ровно восемь решений (точек пересечения) возможно в том случае, если прямая 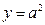 расположена выше прямой
расположена выше прямой 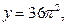 но ниже прямой
но ниже прямой 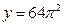 . Следовательно,
. Следовательно, 
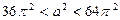 ,
,
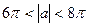 .
.
При 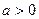
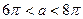 ,
,
при 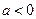
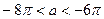 .
.
Ответ: 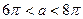 ,
, 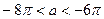
 Решение: 2 способ.
Решение: 2 способ. 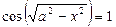 ,
, 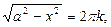
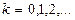 Заметим, что параметр а может принимать как положительные, так и отрицательные значения, но не равен нулю.
Заметим, что параметр а может принимать как положительные, так и отрицательные значения, но не равен нулю.
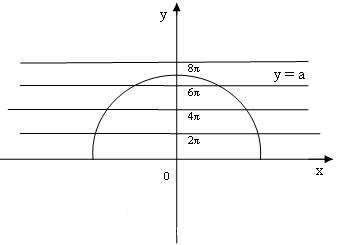
Построим график функции 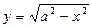 при у>0 , т.е.
при у>0 , т.е. 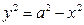 или
или 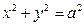 (полуокружность с центром в начале координат) . Графиком второй функции
(полуокружность с центром в начале координат) . Графиком второй функции 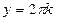 при
при 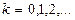 является семейство прямых, параллельных оси ОХ, проходящих через точки с ординатами у=0,
является семейство прямых, параллельных оси ОХ, проходящих через точки с ординатами у=0, 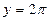 ,
, 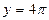 ,
, 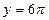 ,
, 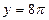 и т.д.
и т.д.
Рассмотрим полуокружность радиуса r=a. Если радиус 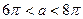 , то полуокружность пересекает серию прямых ровно в восьми точках. Аналогично рассуждаем для случая а<0.
, то полуокружность пересекает серию прямых ровно в восьми точках. Аналогично рассуждаем для случая а<0.
Ответ: 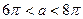 ,
, 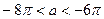
Пример 6: Найдите все значения параметра a, при котором уравнение 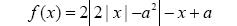 имеет три различных корня.
имеет три различных корня.
Решение:
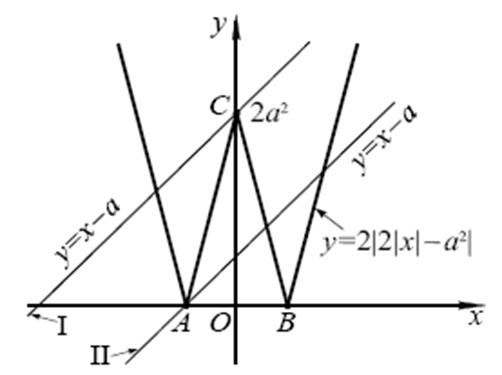
График функции 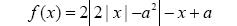 при a≠0 изображен на рисунке. Сразу заметим, что при а=0 уравнение имеет один корень.
при a≠0 изображен на рисунке. Сразу заметим, что при а=0 уравнение имеет один корень.
Из семейства параллельных прямых y=x-a нас интересуют только те, которые пересекают наш график в трёх точках..
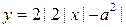 |
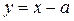 Графики функций и пересекутся в трех точках тогда и только тогда, когда прямая
Графики функций и пересекутся в трех точках тогда и только тогда, когда прямая
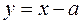 пройдет через точку А или точку С. Во всех остальных случаях количество точек пересечения графиков функций будет или больше, или меньше трех. Определим значения параметра а в первом и во втором случае.
пройдет через точку А или точку С. Во всех остальных случаях количество точек пересечения графиков функций будет или больше, или меньше трех. Определим значения параметра а в первом и во втором случае.
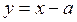 Если прямая проходит через точку А, то из уравнения получаем а=-2. Аналогично с точкой С, получаем a=-0.5
Если прямая проходит через точку А, то из уравнения получаем а=-2. Аналогично с точкой С, получаем a=-0.5
Упражнения
1. Найдите все значения параметра а, при каждом из которых уравнение 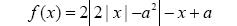 имеет ровно три различных решении.
имеет ровно три различных решении.
2. Найдите все значения параметра а, при которых уравнение 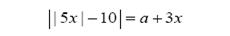 имеет ровно три различных решения.
имеет ровно три различных решения.
Для каждого полученного значения, а найдите все эти решения.
3. Найдите все значения параметра а, при каждом из которых график функции 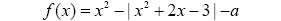 пересекает ось абсцисс более чем в двух различных точках.
пересекает ось абсцисс более чем в двух различных точках.
4. Найдите все значения параметра а, при каждом из которых график функции 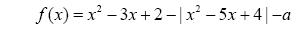 пересекает ось абсцисс менее чем в трёх различных точках.
пересекает ось абсцисс менее чем в трёх различных точках.
5. Сколько решений в зависимости от параметра а имеет уравнение 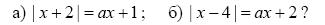
6. Выясните, при каких значениях параметра а уравнение 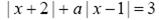 ;
;
а) имеет единственный корень, и найдите его;
б) имеет ровно два корня, и найдите их;
в) имеет бесконечное множество корней.
7. Найдите все значения а, при каждом из которых имеет ровно один корень уравнение
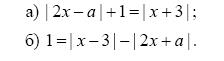
8.Сколько решений в зависимости от значений параметра а имеет уравнение
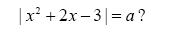
9. Найдите все значения параметра а, при каждом из которых уравнение 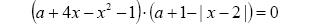 имеет ровно три различных корня.
имеет ровно три различных корня.
10. При каких значениях параметра а уравнение 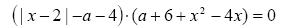 имеет ровно три различных корня.
имеет ровно три различных корня.
11. Найдите все значения параметра а, при каждом из которых уравнение 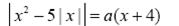 имеет ровно три различных корня.
имеет ровно три различных корня.
12. Найдите все значения параметра а, при которых уравнение 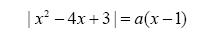 имеет два различных корня. Укажите эти корни.
имеет два различных корня. Укажите эти корни.
13. Найдите все значения параметра а, при каждом из которых уравнение 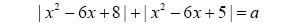 имеет ровно три корня.
имеет ровно три корня.
Ответы
1. -2; -0,5
2. При а=6 , х1= -2, х2 = 0,5, х3 =8; при а=10, х1= -2,5, х2=0, х3=10
3. (-3,5; 1)
4. 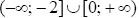
5. При а 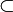 (0,5; 1] - решений нет; при а
(0,5; 1] - решений нет; при а 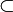 (-∞; -1]
(-∞; -1] 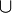 {0.5}
{0.5} 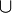 (1; ∞) – одно; при а
(1; ∞) – одно; при а 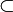 (-1; 0,5) – два: б) при а
(-1; 0,5) – два: б) при а 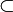 [-1;- 0,5) – решений нет; при а
[-1;- 0,5) – решений нет; при а 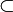 (-∞; -1)
(-∞; -1) 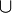 {0.5}
{0.5} 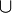 [1; ∞) – одно; при а
[1; ∞) – одно; при а 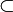 (-0,5; 1) - два
(-0,5; 1) - два
6. а) | а | > 1, х=1; б) | а | <1, х1= 1, х2= а-5/ а+1; в) а=1 и а=-1
7. а) -4, -8; б) -4, -8
8. если а<0, то решений нет; если а=0 или а >4, то – два; если а=4, то – три; если 0< а<4, то - четыре
9. -1
10. -4, -2
11. 0, 1
12. 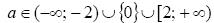 ; х=1, х=а+3
; х=1, х=а+3
13. 5
