D5- для оптимального значения целевой функции
2.Введем исходные данные в созданную форму (рис.7.)
 Рис. 6. Форма для ввода данных. Рис. 6. Форма для ввода данных. | 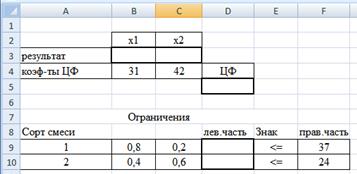 Рис 7. Данные введены. Рис 7. Данные введены. |
3.Введем зависимость для целевой функции
· Курсор в ячейку D5. 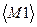 (Обозначим через
(Обозначим через 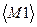 - один щелчок левой кнопкой мыши).
- один щелчок левой кнопкой мыши).
· Курсор на кнопку Мастер функцийfx.  .
.
· На экране диалоговое окно Мастер функций шаг 1 из 2.
· В окне Категория выбрать Математические. 
· В окне Функции выбрать СУММПРОИЗВ. 
· Готово  . На экране появиться диалоговое окноСУММПРОИЗВ, показанное на рис. 8.
. На экране появиться диалоговое окноСУММПРОИЗВ, показанное на рис. 8.
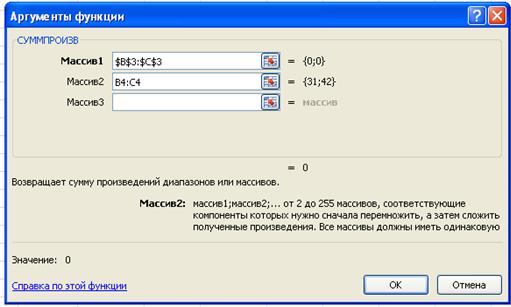
Рис 8. Ввод формулы для вычисления целевой функции.
· Курсор в поле Массив 1 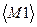 : ввести В3:С3. Во все диалоговые окна адреса удобно вводить не с клавиатуры, а протягиванием мыши (не отпуская левой кнопки) по ячейкам, адреса которых следует указать в этом поле. Чтобы на адресах установить знак $ нажмите на клавиатуре кнопку
: ввести В3:С3. Во все диалоговые окна адреса удобно вводить не с клавиатуры, а протягиванием мыши (не отпуская левой кнопки) по ячейкам, адреса которых следует указать в этом поле. Чтобы на адресах установить знак $ нажмите на клавиатуре кнопку 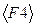 . В результате в поле Массив 1 будут указаны адреса $В$3:$С$3.
. В результате в поле Массив 1 будут указаны адреса $В$3:$С$3.
· Курсор в поле Массив 2 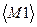 : ввести В4:С4.
: ввести В4:С4.
· Готово  На экране: в ячейку D5 введена формула вычисления целевой функции (Рис. 9.)
На экране: в ячейку D5 введена формула вычисления целевой функции (Рис. 9.)
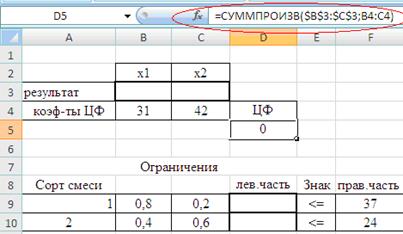
Рис. 9. Ввод формулы в ячейку целевой функции.
4.Аналогично введем зависимости, стоящие в левых частях ограничений:
o Курсор в ячейку D9
o Мастер функций fx/ СУММПРОИЗВ
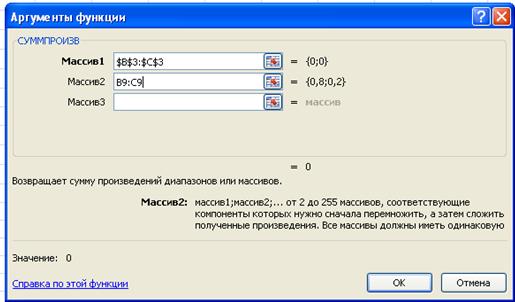
В пустой ячейке D9 появляется посчитанное значение 0 (ячейки В3:С3 пустые - значения переменных равны 0).
Так как структура формул во всех ограничениях одинакова, то формулу можно скопировать:
· Курсор в ячейку D9. 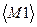
· Выбрать курсором кнопку Копировать.
· Курсор в ячейку D10. 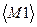
· Выбрать курсором кнопку Вставить. (Можно «протянуть» ячейку D9 в ячейку D10)
На этом ввод зависимостей закончен (Рис. 10).
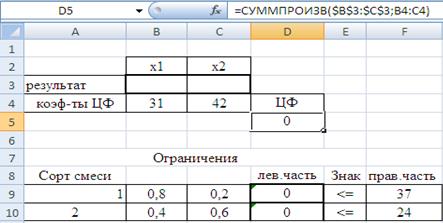
Рис. 10. Ввод зависимостей.
После копирования формул обязательно проверьте адреса!
Замечание:так как во всех зависимостях надо ссылаться на изменяемые ячейки В3:С3, для них использованы абсолютные адреса.
Этап 3. Запуск Поиск решений
После выбора команд Поиск решения появится диалоговое окно Поиск решения (Рис. 11)
· Назначение целевой ячейки: курсор в поле Установить целевую ячейку. 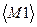 . Курсор в ячейку D5.
. Курсор в ячейку D5.  .
.
· Ввести направление целевой функции: максимальному значению.
· Ввести адреса искомых переменных: курсор в поле Изменяя ячейки. 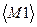 . Выделить мышью ячейки В3:C3.
. Выделить мышью ячейки В3:C3.
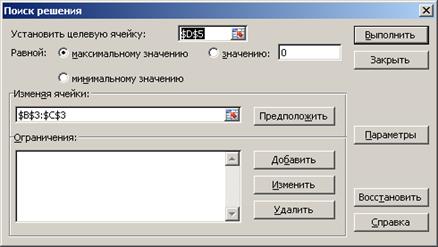
Рис. 11. Подготовка Поиска решения.
· Ввести ограничения:
o курсор в поле Ограничения  . Выбрать режим Добавить
. Выбрать режим Добавить  . Появляется диалоговое окно Добавление ограничений, как показано на рис. 12.
. Появляется диалоговое окно Добавление ограничений, как показано на рис. 12.
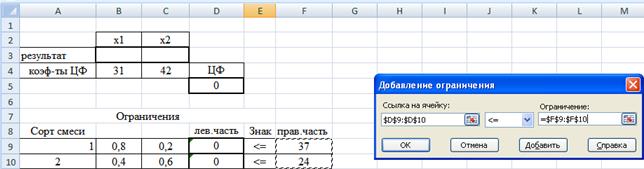
Рис. 12. Ввод ограничений.
o курсор в поле Ссылка на ячейку 
o выбрать мышью ячейки D9:D10
!!! Обратите внимание: указываются адреса ячеек, содержащих формулу.
o ввести знак ограничения <=
o курсор в правое окно Ограничение  .
.
o указать мышью адреса F9:F10
o если ввод ограничений закончен, выберете  , если
, если
надо ввести другие ограничения, то Добавить.
В результате этих действий экран будет выглядеть, как представлено на рис 13.
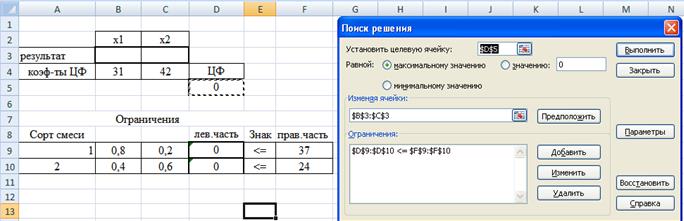
Рис 13. Введены все условия для решения задачи.
· Выбрать параметры модели: рис 4.
Этап 4. Выполнить.
На экране диалоговое окно Результат поиска решения.(рис. 14.)
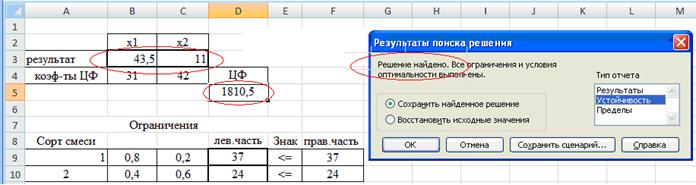
Рис. 14. Решение найдено.
В результате решения получен ответ: максимальное значение целевой функции составит 1810,5 при значениях переменных 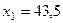 и
и 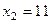 .
.
Вопросы:
1. Какие ресурсы использованы полностью?
2. Измените модель, добавив условие:
1. Спрос на смесь 1 составляет не более 30 ед.; на смесь 2 — не менее 45 ед.(нет решения)
2. Всего смеси надо произвести не более 35ед.((0;35) F=1470)
3. Смеси разных видов должно быть одинаковое количество. ((24;24) F=1752)
