Напряжения и деформации при кручении

Кручение – такой вид деформации, когда в поперечном сечении стержня действуют только крутящий момент М_кр. Величина крутящего момента определяется методом сечений (рис. 5.1).

Σm_z = 0: M_kp = M (5.1)

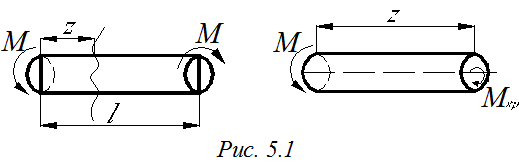Стержень круглого поперечного сечения, испытывающий деформацию кручения, называется валом.

Касательные напряжения при кручении можно найти как:

(5.2)

I_ρ – полярный момент инерции.

Условие прочности при кручении 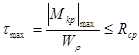(5.3)

– полярный момент сопротивления.

Угол закручивания при кручении определяется как:

(5.4)

GI_ρ – жесткость при кручении (Нм²).

Условие жесткости при кручении (5.5)

[θ] – относительный допускаемый угол закручивания. Величина его определяется нормами проектирования.

Расчет цилиндрических винтовых пружин с малым шагом витка

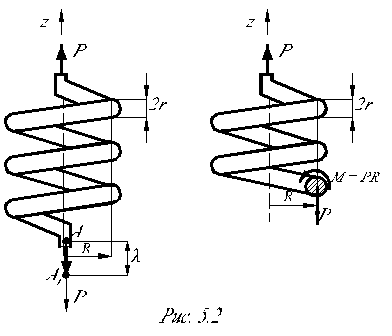
Пружины, у которых угол наклона витка к плоскости, перпендикулярной оси пружины мал, называют пружинами с малым шагом витка. В этом случае полагают, что витки лежат в плоскости, перпендикулярной оси z (рис. 5.2).

Обозначим:

R – радиус витка пружины;

r - радиус проволоки, из которой сделана пружина;

n – количество витков пружины.

Витки пружины работают на срез (Q_y) и кручение (М_кр).

Поэтому касательные напряжения можно найти как:

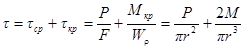(5.6)

Осадка пружины :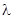

(5.7)

Напряженное состояние в точке

Общие понятия

В соответствии с гипотезой о сплошности материала каждая его частица окружена и взаимодействует с множеством окружающих ее других частиц. Следовательно, если через рассматриваемую точку материала провести бесконечно малые взаимно перпендикулярные площадки, то по ним будут действовать различные напряжения.

Совокупность напряжений, действующих по таким площадкам, представляет собой напряженное состояние в рассматриваемой точке.

Для оценки напряженного состояния в точке вокруг неё выделяют элементарный параллелепипед с размерами граней dx, dy, dz. Ввиду малости параллелепипеда напряжение по его граням распределяется равномерно, а напряженное состояние во всех его точках совпадает с напряженным состоянием в точке к.

По граням параллелепипеда действуют нормальные и касательные напряжения.

Индекс нормального напряжения σ совпадает с направлением соответствующей координатной оси: σ_х, σ_у, σ_z.

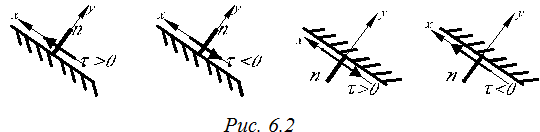Нормальное напряжение считается положительным, когда оно направлено в сторону растяжения (рис.6.1)

Касательное напряжение τ_mn имеет два индекса:

m – соответствует направлению внешней нормали к рассматриваемой площадке;

n – соответствует оси, параллельно которой действуют касательные напряжения τ.

Знак касательного напряжения определяется по правилу внешней нормали «n» (рис.6.2).

На взаимно перпендикулярных площадках соблюдается закон парности касательных напряжений.

τ_xy = τ_yx

τ_yz = τ_zy (6.1)

τ_zx = τ_xz

Различают объемное, плоское и линейное напряженное состояние (рис.6.3)