Обозначение отношений между геометрическими образами

Обозначение	Содержание	Пример символической записи
º	совпадение	(AB) º (CD) – прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки C и D
=	равенство	IABI = ICDI – длина отреза АВ равна длине отрезка CD
^	перпендикулярность	m ^ Р – прямая m перпендикулярна плоскости Р
II	параллельность	а II b – прямые а и b параллельны

Таблица 2

Обозначения теоретико-множественные

Обозначение	Содержание	Пример символической записи в начертательной геометрии
Î	является элементом	D ' b – прямая b проходит через точку D
Ì	включает, содержит	a Ì Q– прямая a принадлежит плоскости Q
É	проходит через	b ÉR – плоскость R проходит через прямую b
∩	пересечение	MN = Q ∩ R – прямая MN есть линия пересечения плоскостей Q и R

МЕТОД ПРОЕКЦИЙ

Основные понятия метода проецирования

В любой науке есть базовые понятия, которые лежат в ее основе. Для начертательной геометрии таким понятием является проецирование.

Проецирование – процесс получения изображения на плоскости.

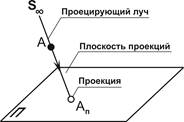Рис.1.1. Метод проецирования

Сущность метода – имеется точка пространства A. Необходимо построить ее изображение на плоскости П. Операция проецирования заключается в проведении через точку А прямой, которая бы пересекала плоскость П. Эта прямая называется проецирующим лучом. Изображение A_п, полученное в результате пересечения плоскости П проецирующим лучом, называется проекцией точки А на плоскости П. А плоскость, на которой получено изображение, называется плоскостью проекций П (рис. 1.1).

Если необходимо получить проекцию более сложного геометрического образа, к примеру треугольника, то проецирующие лучи нужно проводить через три его вершины.

Виды проецирования

В начертательной геометрии различают два основных метода проецирования: центральное (рис. 1.2) и параллельное (рис. 1.3).

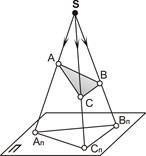
Центральное проецирование.Если все проецирующие лучи исходят из собственной точки S (точки, находящейся в обозримом пространстве), то проецирование называетсяцентральным, а сама точка S – источником проецирующих лучей. Таким образом, аппарат центрального проецирования включает в себя центр проецирования – точку S, проецирующие лучи и плоскость проекций (рис. 1.2). Для проецирования произвольной точки через неё и центр проекций проводят прямую (проецирующий луч). Точка пересечения проецирующего луча с плоскостью проекций и является центральной проекцией заданной точки на выбранной плоскости проекций. На рис.1.2 центральной проекцией точки А является точка А_п, которая находится на пересечении прямой SA с плоскостью П. Следует отметить, что если точки расположены на одной проецирующей прямой, то их проекции совпадают. Такими точками на рис. 1.2 являются – точки B и C; ВÌ(SB), СÌ(SC), B_п=C_п.

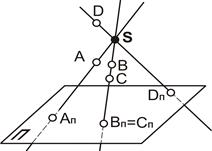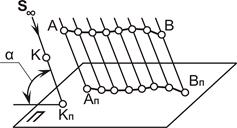Рис. 1.2. Центральное проецирование	Рис. 1.3. Параллельное проецирование

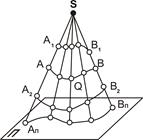
Проекция кривой линии представляет собой линию пересечения проецирующей конической поверхности с плоскостью проекций. Так, на
рис. 1.4, а проецирующая поверхность Q пересекается с плоскостью проекций П по кривой А_пВ_п, являющейся проекцией линии АВ. Однако А_пВ_п – это проекция всех линий, принадлежащих проецирующей поверхности Q (рис. 1.4, а).

Для построения проекций линий, поверхностей или тел часто достаточно построить проекции лишь некоторых характерных точек. Например, при построении на плоскости проекций П проекции треугольника АВС
(рис. 1.4, б) достаточно построить проекции трех его вершин – точки А_п, В_п, С_п.

а	б
Рис. 1.4. Центральное проецирование геометрических объектов: а – проецирование кривых линий; б – проецирование треугольника

Параллельное проецирование. Параллельное проецирование можно рассматривать как частный случай центрального проецирования, при котором центр проекций S удален в бесконечность (рис. 1.3).

При параллельном проецировании применяют параллельные проецирующие лучи, проведенные в заданном направлении относительно плоскости проекций.

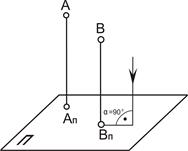
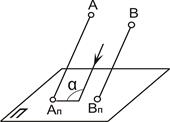
Если направление параллельного проецирования перпендикулярно плоскости проекций, то проецирование называют прямоугольным (ортогональным) (рис. 1.5, а), в остальных случаях – косоугольным (рис. 1.5, б).

а	б
Рис. 1.5. Параллельное проецирование: а – прямоугольное проецирование; б – косоугольное проецирование

технические чертежи получают методом параллельного прямоугольного проецирования, который был впервые систематически изложен Гаспаром Монжем, поэтому его иногда называют методом Монжа. Это наиболее распространенный метод, используемый для технических целей, хотя он не даёт наибольшей наглядности, но вместе с тем ортогональное проецирование имеет ряд преимуществ перед центральным и параллельным косоугольным проецированием:

– простота геометрических построений ортогональных проекций предметов;

– сохранение на проекциях, при определенных условиях, формы и величины линейных и угловых размеров проецируемых предметов.