Некоторые важные примеры приложений.

ЛЕКЦИЯ

Вычисление функций от матриц

Определения функции от матрицы.

Определение 1. Приведем некоторые примеры формул, по которым ведется вычисление основных функций на ЭВМ:

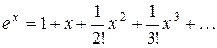( 1)

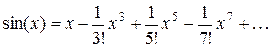( 2)

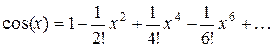, ( 3)

где x – аргумент функции.

Аналогично можно задать функции от матриц:

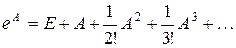( 4)

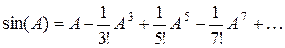( 5)

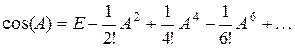, ( 6)

где 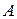– матрица (аргумент функции).

Определение 2. В большинстве случаев, за редким исключением, квадратная матрица 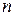-го порядка может быть представлена в виде произведения (разложения):

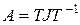, где 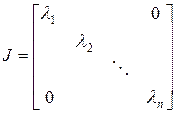, ( 7)

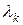– собственные числа матрицы 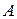; 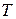– матрица, столбцы которой являются соответствующими собственными векторами матрицы .

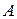Из разложения ( 7) следует:

; ; …

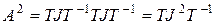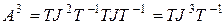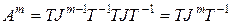, ( 8)

где

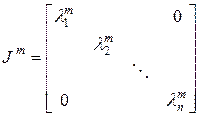. ( 9)

Подставив 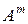в формулы ( 4)-( 6), получим:

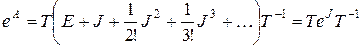; ( 10)

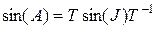; ( 11)

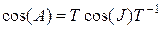, ( 12)

где

; ;

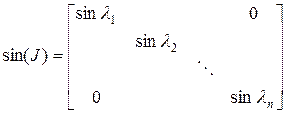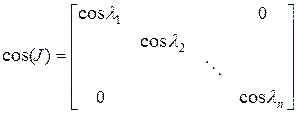. ( 13)

Данные преобразования позволяют записать общую формулу для определения функций от матрицы, которая существенно упрощает процесс вычисления:

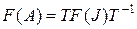, ( 14)

где

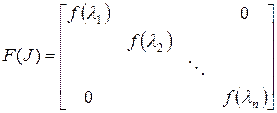; ( 15)

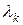– собственные числа матрицы 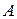, 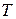– матрица, столбцы которой являются соответствующими собственными векторами матрицы 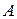, n – порядок квадратной матрицы .

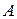Замечание 1. Самый общий случай представления квадратной матрицы в виде произведения также имеет вид жорданова разложения

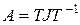( 16)

но при этом матрица Жордана 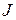имеет квазидиагональный вид:

, ; ,

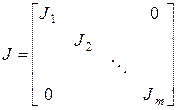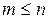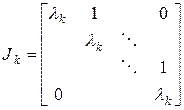где 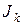– жорданова клетка; матрица 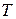состоит из столбцов, часть которых является собственными векторами, а часть присоединенными (или корневыми) векторами, при этом

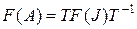, ( 17)

где

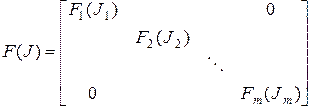; ( 18)

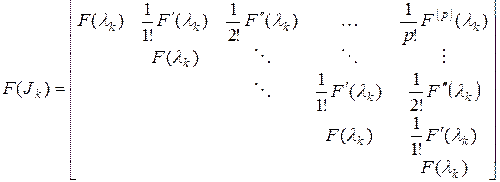, ( 19)

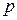– порядок k-ой жордановой клетки.

Более подробно данный вопрос рассматривается в специальной литературе по линейной алгебре.

Дополнительный вид определения функции от матрицы. В случае, если порядки всех жордановых клеток равны единице, тогда:

,

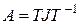где

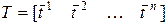, ( 20)

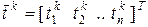– собственный вектор матрицы :

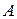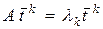, ( 21)

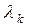– собственное число.

Собственные векторы нормированы, т.е.

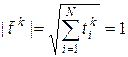. ( 22)

Очевидно, что матрица Жордана 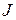представима в виде следующего разложения

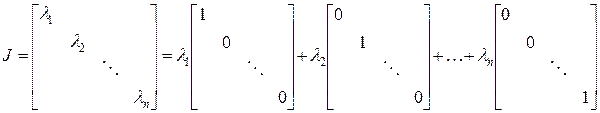. ( 23)

Матрицу 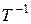можно представить в виде:

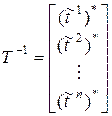, ( 24)

где 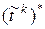– k-я вектор-строка матрицы .

Тогда матрица может быть представлена следующим образом:

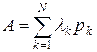, ( 25)

где

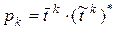( 26)

– оператор проектирования представимый в виде

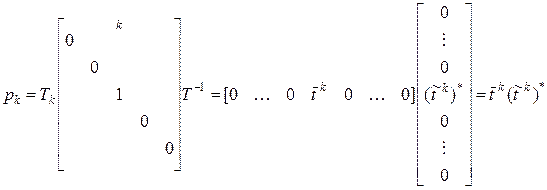. ( 27)

Проверим, покажем, что

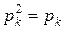. ( 28)

Вследствие ( 26) имеем:

.

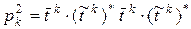Произведение 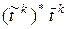является результатом умножения k-ой строки матрицы 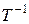на k-й столбец матрицы . В тоже время, как известно, 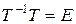. Следовательно, 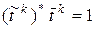, что доказывает формулу ( 28).

Соответственно функция от матрицы будет иметь вид:

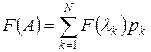( 29)

В частности, справедливы формулы:

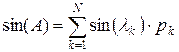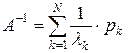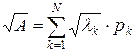; ; . ( 30)

Такая запись применяется, к примеру, для получения общего решения задачи динамики.

Замечание 2. Функции от матриц являются необходимым средством решения систем дифференциальных уравнений (см. примеры ниже).

Некоторые важные примеры приложений.

Пример 1. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений первого порядка вида

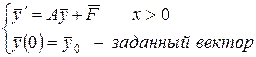( 31)

где

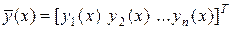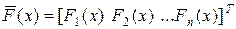; , ( 32)

причем 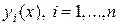– искомые функции; 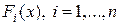– заданные функции; 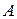– матрица, не зависящая от x.

Общее решение задачи ( 31) определяется формулой:

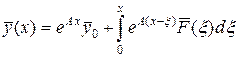. ( 32)

Пример 2. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений второго порядка вида

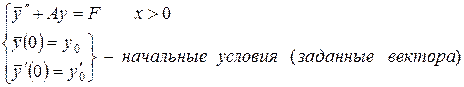( 33)

Пусть 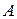– положительно определенная матрица, т.е. все ее собственные числа 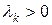. Тогда общее решение ( 33) можно записать в виде:

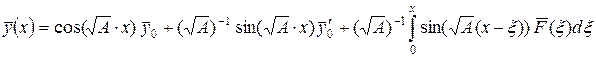. ( 34)

Пример 3. Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений второго порядка вида

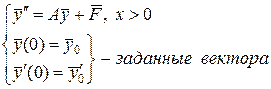( 35)

Общее решение задачи ( 35) определяется формулой:

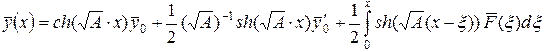, ( 36)

где 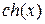и 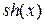– гиперболические синус и косинус от произвольного аргумента.

Замечание 3. В среде МАТЛАБ реализовано вычисление некоторых функций от матриц с помощью обращения к стандартной функции funm:

Function	Syntax for Evaluating Function at Matrix A
exp	funm(A, @exp)
log	funm(A, @log)
sin	funm(A, @sin)
cos	funm(A, @cos)
sinh	funm(A, @sinh)
cosh	funm(A, @cosh)

Кроме того, для вычисления 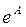, 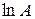и 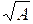можно использовать встроенные функции expm(A), logm(A) и sqrtm(A), соответственно.