Двойственность в нелинейном программировании

Рассмотримнекоторые фундаментальные моменты теории нелинейного программирования. Исходной точкой для них является распространение метода Лагранжа для решения ЗИП с ограничениями в форме неравенств:

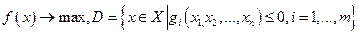(28)

где X - некоторая область в пространстве .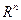

Определим для задачи (28) функцию Лагранжа:

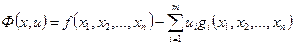.(29)

Определение.Пара векторов 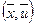называется седловой точкойфункции 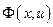некоторой области 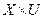, если для любых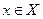

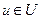
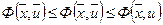. (30)

Неравенства (30) также называют неравенствами седловой точки.

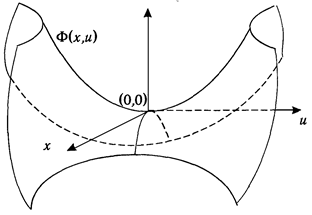
Рис. 2.7

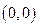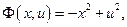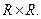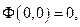
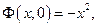
В качестве примера седловой точки может быть приведена точка для функции определенной на множестве Действительно, 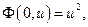а для любых 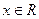и 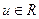выполняются неравенства 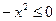и .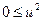

На Рис. 2.7изображен график функции 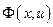(гиперболический параболоид), и, как видно, в окрестности точки он действительно по форме напоминает седло, чем и объясняется происхождение соответствующего термина.

Теорема Куна-Таккера.Центральное место в теории нелинейного программирования занимает теорема Куна - Таккера, которая связывает решение ЗНП с наличием седловой точки у соответствующей функции Лагранжа.

Теорема 2.3.(Достаточное условие экстремума).Если 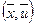- седловая точка функции Лагранжа, в области 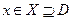, , 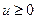mo 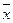является оптимальным планом задачи (28), причем справедливо так называемое правило дополняющей нежесткости

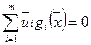. (31)

По определению седловой точки имеем

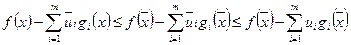(32)

при всех 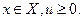Из второго неравенства в (32) следует, что

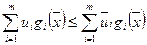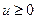, для (33)

Однако (33) может иметь место только тогда, когда 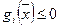при всех 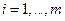. Действительно, если существует такое k, что 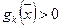, то, положив 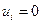для всех 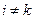и выбрав достаточно большое 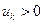, можно добиться того, что значение

,

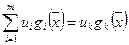окажется больше постоянного выражения

.

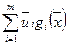Из того, что для всех 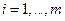выполняются неравенства 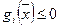следует, что 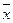является допустимым планом задачи (28).

Если в левую часть неравенства (33) подставить значения 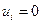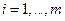.то получим, что

.

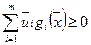С другой стороны из того что, 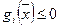и 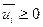, следует оценка

.

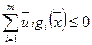Совместное рассмотрение последних двух неравенств приводит к правилу дополняющей нежесткости в точке :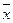

.

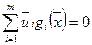Тогда на основании левой части неравенства седловой точки (32) имеем, что для всех 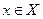(в том числе и для )

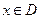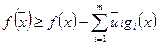
По условию ЗИП для любых 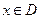верны неравенства 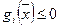, что, в сочетании с условием 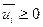, позволяет записать

.

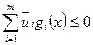Следовательно,

.

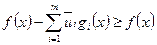Окончательно получаем, что для любых 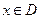справедливо соотношение 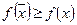, т.е. 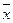- оптимальный план задачи (28).

Утверждение, обратное теореме (3), т. е. необходимое условие экстремума в ЗНП, оказывается верным только при выполнении дополнительных условий, которым должна удовлетворять задача (28). Важнейшим из них является так называемое условие регулярности Слейтера:

Говорят, что функция 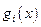, задающая ограничение в задаче (28), удовлетворяет условию регулярности Слейтера, если существует такая точка 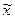, принадлежащая области допустимых, планов D, что

,

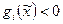т. е. 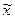является внутренней точкой относительно ограничения 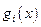. Поэтому данное условие также называют условием телесности.

Вообще говоря, существуют разные варианты необходимого условия Куна-Таккера. Приведем один из них.

Теорема 2.4.(Необходимое условие наличия экстремума) Если 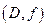является задачей выпуклого программирования с решением 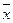, ее целевая функция 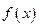и функции ограничений 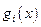- дифференцируемы, нелинейные ограничения в форме неравенств удовлетворяют условию регулярности Слейтера, то существует такой вектор 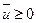, что 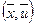- седловая точка функции Лагранжа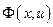

Значение теоремы Куна-Таккера состоит в том, что она позволяет связать процесс решения оптимизационной задачи с поиском седловых точек функции Лагранжа, т. е., грубо говоря, с максимизацией этой функции по х и минимизацией по и.

Определим 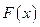какфункцию, ставящую в соответствие каждому значению х минимальное значение функци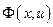и по и:

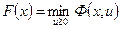
и по аналогии

.

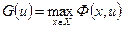Рассмотрим задачу отыскания максимума функции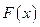

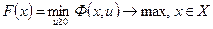(34)

и задачу минимизации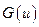

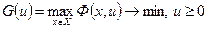. (35)

Очевидно, что

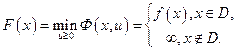
Отсюда следует, что максимум 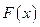находится в допустимой области D и совпадает с максимумом целевой функции 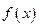задачи (28):

.

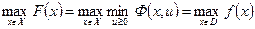Таким образом, задача (34), в определенном смысле, равносильна (28). Аналогичные выводы могут быть получены и для (35). Задачи (34) и (35) образуют двойственную пару. Очевидно, данное отношение является обобщением отношения двойственности для задач линейного программирования. Соответственно, при определенных условиях пара двойственных задач нелинейного программирования обладает свойствами, аналогичными свойствам двойственных линейных задач. В частности, при любых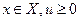

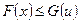.(36)

Условие (36) находит широкое применение при построении оценок в итеративных методах решения оптимизационных задач. Например, если имеется возможность приблизительно решить прямую и двойственную задачи и получить последовательности приближени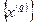й и 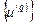, то с помощью неравенств вида

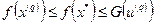
можно определить момент остановки вычислительной процедуры.

В заключение отметим, что возможен вариант вывода выражений для целевых функций и ограничений пары двойственных задач линейного программирования из общего определения отношения двойственности для нелинейных задач. Также отметим, что в процессе формирования нелинейных двойственных задач существует большая неоднозначность: их вид можно варьировать, включая в множество X часть ограничений 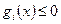.