Основы теории и практики моделирования
3х летний курс обучения
Данилкин Вадим Юрьевич шифр 558
Город Шатура
Вариант контрольного задания определяется суммой двух последних цифр шифра студента и указан в первой строке таблицы. Во второй строке таблицы указан номер первого задания (В1) по варианту, в третьей – второго задания (В2).
Задание 1
Вариант 13
В1 – 8
Привести к канонической форме следующие задачи линейного программирования.
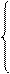2x1 - x2 - x3 + x4≤6
x1 + 2x2 + x3 - x4≥8
3x1 - x2 + 2x3 + 2x4≤10
- x1 + 3x2 + 5x3 - 3x4=15
Х1 ≥0, Х2≥0, Х3≥0, Х4≥0
F(X) = - x1 + 2x2 - x3 + x4 ---> min
Симплекс-метод.
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим минимальное значение целевой функции F(X) = - x1 + 2x2 - x3 + x4 при следующих условиях-ограничений.
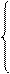2x1 - x2 - x3 + x4≤6
x1 + 2x2 + x3 - x4≥8
3x1 - x2 + 2x3 + 2x4≤10
- x1 + 3x2 + 5x3 - 3x4=15
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≤) вводим базисную переменную x5. В 2-м неравенстве смысла (≥) вводим базисную переменную x6 со знаком минус. В 3-м неравенстве смысла (≤) вводим базисную переменную x7.
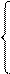2x1-1x2-1x3 + 1x4 + 1x5 + 0x6 + 0x7 = 6
1x1 + 2x2 + 1x3-1x4 + 0x5-1x6 + 0x7 = 8
3x1-1x2 + 2x3 + 2x4 + 0x5 + 0x6 + 1x7 = 10
-1x1 + 3x2 + 5x3-3x4 + 0x5 + 0x6 + 0x7 = 15
Введем искусственные переменные x: в 2-м равенстве вводим переменную x8; в 4-м равенстве вводим переменную x9;
2x1-1x2-1x3 + 1x4 + 1x5 + 0x6 + 0x7 + 0x8 + 0x9 = 6
1x1 + 2x2 + 1x3-1x4 + 0x5-1x6 + 0x7 + 1x8 + 0x9 = 8
3x1-1x2 + 2x3 + 2x4 + 0x5 + 0x6 + 1x7 + 0x8 + 0x9 = 10
-1x1 + 3x2 + 5x3-3x4 + 0x5 + 0x6 + 0x7 + 0x8 + 1x9 = 15
Для постановки задачи на минимум целевую функцию запишем так:
F(X) = -1x1+2x2-1x3+x4+Mx8+Mx9 → min
За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый штраф величиной М, очень большое положительное число, которое обычно не задается.
Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.
Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.
Из уравнений выражаем искусственные переменные:
x8 = 8-x1-2x2-x3+x4+x6
x9 = 15+x1-3x2-5x3+3x4
которые подставим в целевую функцию:
F(X) = -x1 + 2x2-x3 + x4 + M(8-x1-2x2-x3+x4+x6) + M(15+x1-3x2-5x3+3x4) → min
или
F(X) = (-1)x1+(2-5M)x2+(-1-6M)x3+(1+4M)x4+(M)x6+(23M) → min
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
| -1 | -1 | |||||||
| -1 | -1 | |||||||
| -1 | ||||||||
| -1 | -3 |
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Экономический смысл дополнительных переменных: дополнительные перемены задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
Решим систему уравнений относительно базисных переменных: x5, x8, x7, x9
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,0,0,6,0,10,8,15)
Базисное решение называется допустимым, если оно неотрицательно.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 |
| x5 | -1 | -1 | ||||||||
| x8 | -1 | -1 | ||||||||
| x7 | -1 | |||||||||
| x9 | -1 | -3 | ||||||||
| F(X0) | 23M | -2+5M | 1+6M | -1-4M | -M |
Переходим к основному алгоритму симплекс-метода.
Итерация №0.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент .
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai3
и из них выберем наименьшее:
min (- , 8 : 1 , 10 : 2 , 15 : 5 ) = 3
Следовательно, 4-ая строка является ведущей.
Разрешающий элемент равен (5) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | min |
| x5 | -1 | -1 | - | ||||||||
| x8 | -1 | -1 | |||||||||
| x7 | -1 | ||||||||||
| x9 | -1 | -3 | |||||||||
| F(X1) | 23M | -2+5M | 1+6M | -1-4M | -M |
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x9 в план 1 войдет переменная x3.
Строка, соответствующая переменной x3 в плане 1, получена в результате деления всех элементов строки x9 плана 0 на разрешающий элемент РЭ=5
На месте разрешающего элемента в плане 1 получаем 1.
В остальных клетках столбца x3 плана 1 записываем нули.
Таким образом, в новом плане 1 заполнены строка x3 и столбец x3.
Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
СТЭ - элемент старого плана, РЭ - разрешающий элемент (5), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
Получаем новую симплекс-таблицу:
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 |
| x5 | 9/5 | -2/5 | 2/5 | 1/5 | ||||||
| x8 | 6/5 | 7/5 | -2/5 | -1 | -1/5 | |||||
| x7 | 17/5 | -11/5 | 16/5 | -2/5 | ||||||
| x3 | -1/5 | 3/5 | -3/5 | 1/5 | ||||||
| F(X1) | -3+5M | 11/5+11/5M | -23/5+12/5M | -2/5-2/5M | -M | -1/5-11/5M |
Итерация №1.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент .
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai2
и из них выберем наименьшее:
min (- , 5 : 12/5 , - , 3 : 3/5 ) = 34/7
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (12/5) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | min |
| x5 | 14/5 | -2/5 | 2/5 | 1/5 | - | ||||||
| x8 | 11/5 | 12/5 | -2/5 | -1 | -1/5 | 34/7 | |||||
| x7 | 32/5 | -21/5 | 31/5 | -2/5 | - | ||||||
| x3 | -1/5 | 3/5 | -3/5 | 1/5 | |||||||
| F(X2) | -3+5M | 11/5+11/5M | -23/5+12/5M | -2/5-2/5M | -M | -1/5-11/5M |
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x8 в план 2 войдет переменная x2.
Строка, соответствующая переменной x2 в плане 2, получена в результате деления всех элементов строки x8 плана 1 на разрешающий элемент РЭ=12/5
На месте разрешающего элемента в плане 2 получаем 1.
В остальных клетках столбца x2 плана 2 записываем нули.
Таким образом, в новом плане 2 заполнены строка x2 и столбец x2.
Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую симплекс-таблицу:
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 |
| x5 | 73/7 | 15/7 | 2/7 | -2/7 | 2/7 | 1/7 | ||||
| x2 | 25/7 | 6/7 | -2/7 | -5/7 | 5/7 | -1/7 | ||||
| x7 | 83/7 | 37/7 | 18/7 | -11/7 | 11/7 | -5/7 | ||||
| x3 | 6/7 | -5/7 | -3/7 | 3/7 | -3/7 | 2/7 | ||||
| F(X2) | 62/7 | 33/7 | -11/7 | -16/7 | 16/7-M | -4/7-M |
Итерация №2.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент .
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai1
и из них выберем наименьшее:
min (103/7 : 21/7 , 34/7 : 6/7 , 116/7 : 52/7 , - ) = 29/37
Следовательно, 3-ая строка является ведущей.
Разрешающий элемент равен (52/7) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | min |
| x5 | 103/7 | 21/7 | 2/7 | -2/7 | 2/7 | 1/7 | 413/15 | ||||
| x2 | 34/7 | 6/7 | -2/7 | -5/7 | 5/7 | -1/7 | 41/6 | ||||
| x7 | 116/7 | 52/7 | 24/7 | -14/7 | 14/7 | -5/7 | 29/37 | ||||
| x3 | 6/7 | -5/7 | -3/7 | 3/7 | -3/7 | 2/7 | - | ||||
| F(X3) | 62/7 | 33/7 | -11/7 | -16/7 | 16/7-M | -4/7-M |
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x7 в план 3 войдет переменная x1.
Строка, соответствующая переменной x1 в плане 3, получена в результате деления всех элементов строки x7 плана 2 на разрешающий элемент РЭ=52/7
На месте разрешающего элемента в плане 3 получаем 1.
В остальных клетках столбца x1 плана 3 записываем нули.
Таким образом, в новом плане 3 заполнены строка x1 и столбец x1.
Все остальные элементы нового плана 3, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую симплекс-таблицу:
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 |
| x5 | 208/37 | -28/37 | 13/37 | -15/37 | -13/37 | 16/37 | ||||
| x2 | 61/37 | -26/37 | -17/37 | -6/37 | 17/37 | -1/37 | ||||
| x1 | 83/37 | 18/37 | -11/37 | 7/37 | 11/37 | -5/37 | ||||
| x3 | 91/37 | -3/37 | 8/37 | 5/37 | -8/37 | 7/37 | ||||
| F(X3) | -115/37 | -230/37 | -31/37 | -24/37 | 31/37-M | -4/37-M |
1. Проверка критерия оптимальности.
Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
| Базис | B | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 |
| x5 | 208/37 | -28/37 | 13/37 | -15/37 | -13/37 | 16/37 | ||||
| x2 | 61/37 | -26/37 | -17/37 | -6/37 | 17/37 | -1/37 | ||||
| x1 | 83/37 | 18/37 | -11/37 | 7/37 | 11/37 | -5/37 | ||||
| x3 | 91/37 | -3/37 | 8/37 | 5/37 | -8/37 | 7/37 | ||||
| F(X4) | -115/37 | -230/37 | -31/37 | -24/37 | 31/37-M | -4/37-M |
Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым.
Оптимальный план можно записать так:
x2 = 124/37
x1 = 29/37
x3 = 217/37
F(X) = 2•124/37 -1•29/37 -1•217/37 = -115/37
Анализ оптимального плана.
В оптимальный план вошла дополнительная переменная x5. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 1-го вида в количестве 523/37
Значение 0 в столбце x1 означает, что использование x1 - выгодно.
Значение 0 в столбце x2 означает, что использование x2 - выгодно.
Значение 0 в столбце x3 означает, что использование x3 - выгодно.
Значение -230/37> 0 в столбце x4 означает, что использование x4 - не выгодно.
Значение -31/37 в столбце x6 означает, что теневая цена (двойственная оценка) равна -31/37.
Значение -24/37 в столбце x7 означает, что теневая цена (двойственная оценка) равна -24/37.
Значение 31/37-1M в столбце x8 означает, что теневая цена (двойственная оценка) равна 31/37-1M.
Значение -4/37-1M в столбце x9 означает, что теневая цена (двойственная оценка) равна -4/37-1M.
Задание 2
Вариант 13
В2 – 11
 Bi Аi | B1 | B2 | B3 | B4 | B5 | Запасы ai |
| А1 | 80 2 | 40 4 | 1 | 6 | 7 | |
| А2 | 3 | 20 3 | 70 5 | 20 4 | 2 | |
| А3 | 8 | 9 | 6 | 80 3 3 | 50 4 4 | |
| Потребности bj |
Получил 7 заполненных клеток – данный план является опорным
(m+n-1=5+3-1=7).
Вычислю общую сумму затрат на перевозки груза по этому плану:
Z1= 80*2+40*4+20*3+70*5+20*4+80*3+50*4=1250
| Bi Аi | B1 | B2 | B3 | B4 | B5 | Запасы ai |
| А1 | 50 2 | 4 | 70 1 | 6 | 7 | |
| А2 | 30 3 | 30 3 | 5 | 4 | 50 2 | |
| А3 | 8 | 30 9 | 6 | 100 4 3 | 4 | |
| Потребности bj |
Получил 7 заполненных клеток – данный план является опорным
(m+n-1=5+3-1=7).
Вычислю общую сумму затрат на перевозки груза по этому плану:
Z2= 50*2+30*3+30*3+30*9+70*1+100*4+50*2=1120