Трансформатор с линейными характеристиками
Одним из важнейших элементов электрической цепи в котором используется магнитная связь между контурами, является трансформатор. Трансформаторы могут иметь различное назначение, однако чаще всего они применяются для преобразования величины переменного напряжения или тока. Такое преобразование необходимо, например, в том случае, когда напряжение источника энергии отличается от напряжения, на которое рассчитан приемник энергии. Трансформаторы состоят из двух или нескольких индуктивно связанных обмоток. Здесь мы ограничимся рассмотрением простейшего двухобмоточного трансформатора (рис. 9.5). В реальном трансформаторе магнитная проницаемость 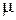 материала сердечника зависит от напряженности магнитного поля. Приняв допущение
материала сердечника зависит от напряженности магнитного поля. Приняв допущение 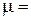 const, будем в дальнейшем рассматривать так называемый линейный трансформатор, процессы в котором описываются линейными уравнениями. Полученные при таком подходе результаты в первом приближении могут быть использованы и для описания режимов в трансформаторе с ненасыщенным ферромагнитным сердечником.
const, будем в дальнейшем рассматривать так называемый линейный трансформатор, процессы в котором описываются линейными уравнениями. Полученные при таком подходе результаты в первом приближении могут быть использованы и для описания режимов в трансформаторе с ненасыщенным ферромагнитным сердечником.
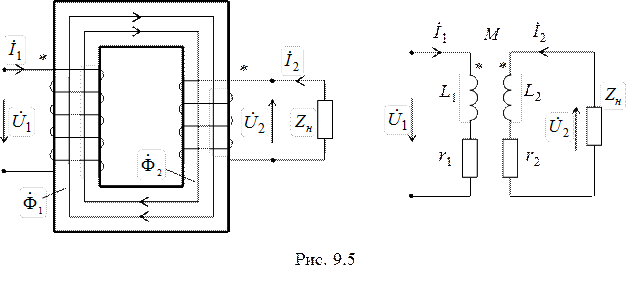 Промаркируем обмотки и выберем условно положительные направления токов так, как это показано на рисунке. Обмотку трансформатора, к которой приложено напряжение источника
Промаркируем обмотки и выберем условно положительные направления токов так, как это показано на рисунке. Обмотку трансформатора, к которой приложено напряжение источника 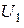 , будем называть первичной, а обмотку, к которой присоединена нагрузка, - вторичной.
, будем называть первичной, а обмотку, к которой присоединена нагрузка, - вторичной.
Магнитные потоки, создаваемые токами первичной и вторичной обмоток, при выбранном направлении токов совпадают по направлению. Это
означает, что взаимная индуктивность 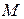 между обмотками положительна.
между обмотками положительна.
Обозначим активные сопротивления обмоток 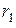 и
и 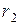 , а их индуктивности
, а их индуктивности 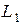 и
и 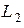 . Пусть вторичная обмотка нагружена на сопротивление
. Пусть вторичная обмотка нагружена на сопротивление 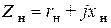 . Вводя обозначения
. Вводя обозначения
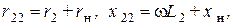
запишем уравнения второго закона Кирхгофа для первичного и вторичного контуров
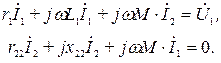
Построим векторную диаграмму токов и напряжений линейного трансформатора для случая 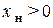 . Для этого в произвольном направлении отложим вектор
. Для этого в произвольном направлении отложим вектор 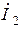 ,
,
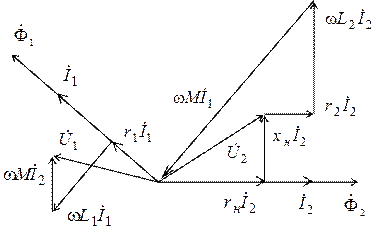
после чего на диаграмме однозначно можно отложить вектора 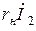 ,
, 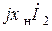 ,
,  ,
, 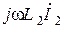 . Соединив конец вектора
. Соединив конец вектора 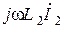 и начальную точку векторной диаграммы, получим, как следует из второго уравнения, вектор
и начальную точку векторной диаграммы, получим, как следует из второго уравнения, вектор 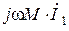 . Разделив напряжение
. Разделив напряжение  на
на 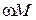 , определим значение тока
, определим значение тока 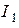 . Вектор
. Вектор 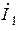 отложим под углом
отложим под углом 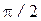 к вектору
к вектору 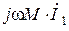 . Затем построим векторы
. Затем построим векторы 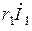 ,
, 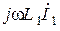 и
и 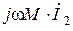 . Их сумма равна вектору входного напряжения
. Их сумма равна вектору входного напряжения 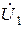 .
.
Как следует из векторной диаграммы, токи в первичной и вторичной обмотках находятся практически в противофазе. Это говорит о том, что ток нагрузки оказывает размагничивающее воздействие на сердечник трансформатора (магнитные потоки пропорциональны создающим их токам и на векторной диаграмме направлены в ту же сторону, что и вектора токов).
Разрешив систему уравнений относительно тока 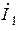 , получим:
, получим:
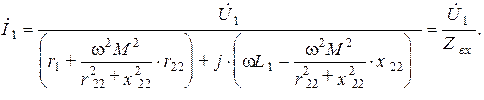
Величина 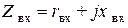 представляет собой входное сопротивление нагруженного трансформатора. Сопротивления
представляет собой входное сопротивление нагруженного трансформатора. Сопротивления 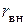 и
и 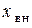 , равные соответственно
, равные соответственно
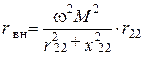 и
и 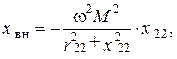
зависят от параметров нагрузки и называются вносимыми активным и реактивным сопротивлениями. Вносимое активное сопротивление всегда больше нуля. В нем поглощается энергия, передаваемая из первичной цепи во вторичную. Вносимое реактивное сопротивление имеет знак, противоположный 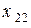 .
.
Рассмотренная схема трансформатора может быть заменена эквивалентной схемой без индуктивной связи. Для этого представим уравнения трансформатора в виде
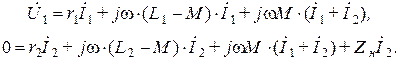
Последние уравнения можно рассматривать как систему уравнений, сформированную по второму закону Кирхгофа для цепи, схема которой приведена на рисунке.
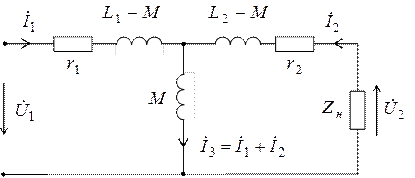
Такая схема замещения используется иногда в практике расчета электрических цепей. Следует отметить, что в подобной схеме замещения величина индуктивности может становиться отрицательной, так как взаимная индуктивность может оказаться больше, чем индуктивность одной из обмоток трансформатора.
Идеальный трансформатор
Идеальным называют трансформатор для которого при любых сопротивлениях нагрузки отношение первичного и вторичного комплексных напряжений и отношение вторичного и первичного комплексных токов постоянны и равны действительному числу
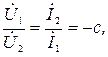 (*)
(*)
где параметр 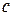 носит название коэффициента трансформации.
носит название коэффициента трансформации.
Запишем уравнения трансформатора в предельном идеализированном случае
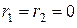 и
и 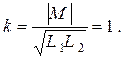
Для схемы, представленной на рис. 9.5, имеем:
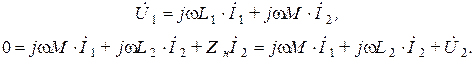
Выразим 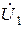 и
и 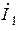 через
через 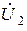 и
и 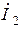 :
:
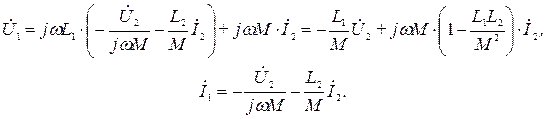
Легко заметить, что при 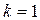 выполняется равенство
выполняется равенство 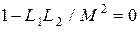 , и тогда, обозначая
, и тогда, обозначая 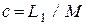 , запишем
, запишем
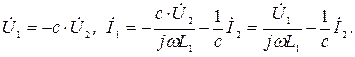
Трансформатор, для которого справедливы полученные уравнения, называют совершенным трансформатором.
Если к вышеуказанным условиям добавить дополнительное условие 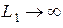 , то в выражении для тока
, то в выражении для тока 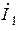 слагаемым
слагаемым 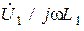 можно пренебречь в сравнении с
можно пренебречь в сравнении с 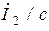 . В этом случае приходим к соотношениям (*), определяющим идеальный трансформатор.
. В этом случае приходим к соотношениям (*), определяющим идеальный трансформатор.
Отметим, что для идеального трансформатора коэффициент трансформации может быть найден как отношение числа витков вторичной и
первичной обмоток
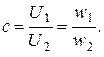
При 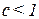 трансформатор называют повышающим, при
трансформатор называют повышающим, при 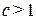 - понижающим.
- понижающим.
Часто используемым на практике свойством идеального трансформатора является свойство преобразования входного сопротивления. Пусть к вторичным выводам идеального трансформатора присоединена нагрузка с комплексным сопротивлением 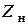 . Тогда для входного сопротивления идеального трансформатора можно записать
. Тогда для входного сопротивления идеального трансформатора можно записать
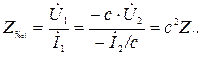
Так как 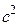 может быть больше или меньше единицы, то входное сопротивление нагруженного трансформатора может быть больше или меньше сопротивления нагрузки.
может быть больше или меньше единицы, то входное сопротивление нагруженного трансформатора может быть больше или меньше сопротивления нагрузки.
Пример. Важным практическим случаем применения трансформаторов является передача максимально возможной мощности от источника к потребителю (согласование нагрузки и источника). Пусть источник характеризуется величиной э.д.с. 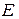 и внутренним сопротивлением
и внутренним сопротивлением  , а приемник сопротивлением
, а приемник сопротивлением 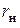 . При непосредственном подключении нагрузки к источнику в нагрузке выделится мощность
. При непосредственном подключении нагрузки к источнику в нагрузке выделится мощность
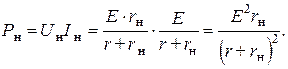 (*)
(*)
Повысить мощность, выделяемую в нагрузке, можно введением в схему трансформатора
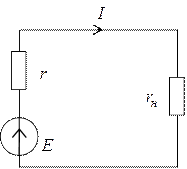
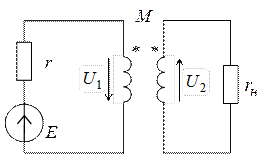
Будем считать трансформатор идеальным, тогда
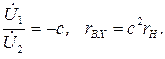
Напряжение на первичной и вторичной обмотках будут равны соответственно
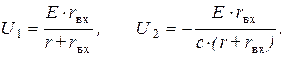
Мощность, выделяемая в нагрузке, определится соотношением
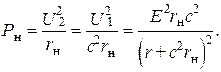
Максимального значения мощность достигает тогда, когда производная 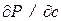 обратится в нуль:
обратится в нуль:
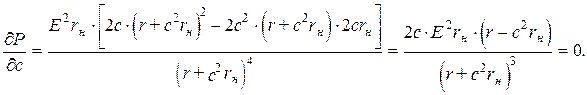
Отсюда следует
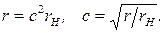
При полученном значении коэффициента трансформации мощность в нагрузке будет равна
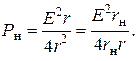 **)
**)
Эта мощность всегда больше или равна мощности, рассеиваемой в нагрузке без трансформатора. Это следует из того, что числители двух сравниваемых выражений для мощности (*) и (**) одинаковы, а для знаменателей выполняются соотношения
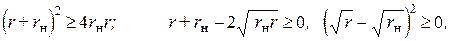
что справедливо при любых значениях параметров источника и нагрузки.
Отметим, что режим передачи максимальной мощности в нагрузку соответствует равенству внутреннего сопротивления  источника и входного сопротивления трансформатора. Таким образом, применение согласующего трансформатора всегда за исключением случая
источника и входного сопротивления трансформатора. Таким образом, применение согласующего трансформатора всегда за исключением случая 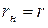 позволяет отбирать большую мощность от источника.
позволяет отбирать большую мощность от источника.
