Invers_Gauss(n, a, invert);
Иркутск
Лучников В.А. Сборник комьютерных программ (в помощь дипломнику). Учебное пособие – Иркутск: ИрГУПС, 2013.-119 с.
Учебное пособие предназначено для студентов специальностей “Информационные системы и технологии”, “Программная инженерия” и “Информационная безопасность”. Оно может быть также полезно для студентов других специальностей, изучающих программирование и использующих его в решении прикладных задач при выполнении дипломных и курсовых работ по специальным дисциплинам.
Учебное пособие содержит тридцать три компьютерные программы на языке Си с примерами их использования. Программы охватывают широкий спектр решаемых задач: матрицы, решение систем линейных и нелинейных алгебраических уравнений, интерполяция, аппроксимация, минимизация, динамические системы, интегрирование, графы. Изложение материала опирается на учебник автора “Программирование на языке Си”.
Данное учебное пособие является шестым в серии учебных пособий по программированию на алгоритмических языках высокого уровня, написанных автором.
Содержание
Вычисление определителя матрицы методом Гаусса 5
Вычисление обратной матрицы методом Гаусса 7
Решение системы линейных алгебраических уравнений
методом Гаусса с выбором главного элемента по всей матрице 9
Решение системы линейных алгебраических уравнений
методом Гаусса по схеме Халецкого 12
Решение системы линейных алгебраических уравнений
итерационным методом Гаусса-Зайделя 15
Решение системы несовместных линейных уравнений
методом наименьших квадратов 18
Решение системы нелинейных и трансцендентных уравнений
методом Стеффенсена 21
Решение избыточной системы нелинейных и трансцендентных уравнений
обобщенным методом Ньютона 24
Вычисление комплексных корней алгебраического уравнения
методом Ньютона-Рафсона 27
Вычисление комплексных корней алгебраического уравнения
модифицированным методом Берстоу 29
Вычисление коэффициентов интерполяционного полинома Лагранжа 31
Интерполяция функций, заданных аналитически, рядом Фурье 33
Интерполяция табличных функций рациональной дробью 36
Аппроксимация табличных функций степенным полиномом
методом наименьших квадратов 39
Аппроксимация табличных функций суммой линейно независимых функций
методом наименьших квадратов 42
Аппроксимация функций, заданных аналитически, степенным полиномом
методом наименьших квадратов 46
Аппроксимация функций, заданных аналитически,
многочленами Чебышева 49
Аппроксимация табличных функций сплайн-функциями 53
Аппроксимация дробно-рациональной функции
понижением степеней ее числителя и знаменателя 56
Приведение квадратной матрицы к форме Гессенбергера
и вычисление ее собственных значений 59
Вычисление коэффициентов характеристического полинома
и обратной матрицы методом Леверрье-Фаддеева 62
Вычисление коэффициентов характеристического полинома матрицы
методом Данилевского (приведение матрицы к форме Фробениуса) 65
Разложение действительной неособенной квадратной матрицы
на произведение двух треугольных (LU-разложение) 68
Минимизация функции многих переменных
модифицированным методом Пауэлла 71
Минимизация функции многих переменных
методом Давидона-Флетчера-Пауэлла 74
Решение системы обыкновенных дифференциальных уравнений
методом Рунге-Кутта четвертого порядка
с постоянным шагом интегрирования 77
Вывод графиков функций 83
Расчет матричной передаточной функции динамической системы
по уравнениям состояния 90
Определение дискретного аналога линейной динамической системы 96
Определение дискретного аналога передаточной функции
методом Тастина 101
Расчет выходного сигнала динамической системы,
заданной передаточной функцией 104
Вычисление определенного интеграла методом Ньютона-Котеса 111
Топологический анализ ориентированных графов 114
Вычисление определителя матрицы
методом Гаусса
В головной программе необходимо:
- описать прототип функции вычисления определителя:
int determinant_Gauss(int n, float a[n][n], float *det);
- ввести значение переменной n – размер матрицы,
- описать исходную матрицу:
float a[n][n];
- ввести матрицуa[n][n],
- обратиться к программе вычисления определителя:
determinant_Gauss(n, a, &det);
- вывести на экран терминала (в текстовый файл) значение определителя det.
Пример:вычислить определитель матрицы
1 1 1 1
a[3][3] = 1 2 3 4
1 3 6 10
1 4 10 20
В этом случае n=4.
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
int determinant_Gauss(int n, float a[n][n], float *det);
int main(int argc, char **argv)
{
int n;// размер матрицы
float det;// определитель матрицы
int i,j;// рабочие переменные
printf("\n Razmer matricy n=");
scanf("%d", &n);
float a[n][n];// исходная матрица
printf("\n Vvedite ichodn. matrizu:\n");
for (i=0; i<n; i++)
{
printf("\n stroka %d (%d chisel) :\n", i+1, n);
for (j=0; j<n; j++)
scanf("%f", &a[i][j]);
}
printf("\n");
determinant_Gauss(n, a, &det);
printf("\n Znachenie opredelitelja = %f\n", det);
Return 0;
}
Результат решения задачи:
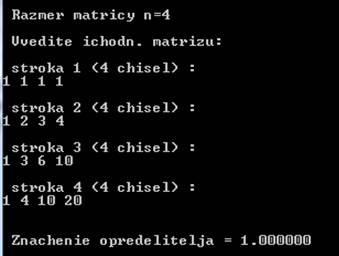
Вычисление обратной матрицы
методом Гаусса
В головной программе необходимо:
- описать прототип функции вычисление обратной матрицы:
int invers_Gauss(int n, float a[n][n], float invert[n][n]);
- ввести значение переменной n – размер матрицы,
- описать исходную и обратную матрицы:
float a[n][n], invert[n][n];
- ввести матрицуa[n][n],
- обратиться к программе вычисления обратной матрицы:
invers_Gauss(n, a, invert);
- вывести на экран терминала (в текстовый файл) вычисленную обратную матрицу.
Пример:вычислить обратную матрицу для исходной матрицы
1 1 1 1
a[3][3] = 1 2 3 4
1 3 6 10
1 4 10 20
В этом случае n=4.
Головная программа:
#include <stdio.h>
#include <math.h>
#include <conio.h>
int invers_Gauss(int n, float a[n][n], float invert[n][n]);
int main(int argc, char **argv)
{
int n;// размер матрицы
int i,j;// рабочие переменные
printf("\n Razmer matricy n=");
scanf("%d", &n);
float a[n][n];// исходная матрица
float invert[n][n];// обратная матрица
printf("\n Vvedite ichodn. matriсu:\n");
for (i=0; i<n; i++)
{
printf("\n stroka %d (%d chisel) :\n", i+1, n);
for (j=0; j<n; j++)
scanf("%f", &a[i][j]);
}
printf("\n");
