Простая эконометрическая модель (Простая регрессия)
Простейшим соотношением между двумя переменными является линейная связь между ними, которая описывается линейной функцией и называется простой линейной регрессией.
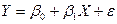 . (2.5)
. (2.5)
где 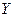 – результативный признак, или зависимая переменная, Х – объясняющая переменная, e - случайная переменная (возмущение), b0, b1 – неизвестные параметры модели.
– результативный признак, или зависимая переменная, Х – объясняющая переменная, e - случайная переменная (возмущение), b0, b1 – неизвестные параметры модели.
Таким образом, зависимая переменная Y представляется как сумма детерминированной ( 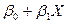 ) и случайной (e) составляющих и является величиной случайной (тогда как Х предполагается детерминированной величиной).
) и случайной (e) составляющих и является величиной случайной (тогда как Х предполагается детерминированной величиной).
Истинные значения параметров b0 и b1 вычислить невозможно, поскольку обычно в распоряжении исследователя находится ограниченное число наблюдений, поэтому неизвестные параметры регрессии подлежат оцениванию по определенной процедуре. Оценки параметров будем обозначать через b0 и b1 соответственно. Тогда уравнение парной регрессии
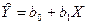 (2.6)
(2.6)
будет являться оценкой модели (2.5).
В этом уравнении b0 – постоянная регрессии (свободный член). Ее можно представить в виде коэффициента при фиктивной переменной, тождественно равной 1. Постоянная b0 определяет точку пересечения прямой регрессии с осью ординат (рис.1).
 Y
Y 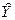

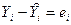
 |
 Yi
Yi
 j b1
j b1
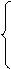

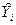
b0

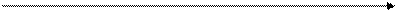 |
1 Xi X
Рис.1 Регрессионная прямая
Так как в соответствии с общим истолкованием уравнения регрессии b0 является средним значением Y в точке X=0, то, очевидно, что экономическая интерпретация b0 часто очень затруднительна или вообще невозможна. Но, благодаря постоянной b0, которая выполняет в уравнении регрессии функцию выравнивания, линия регрессии неошибочна.
Для большинства практических исследований особый интерес представляют величины b1 и 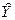 . Коэффициент b1 называют коэффициентом регрессии. Он характеризует наклон прямой к оси абсцисс и равняется тангенсу угла наклона j (рис.1). Согласно (2.6) b1 показывает, насколько в среднем изменится Y при изменении Х на одну единицу. Знак b1 определяет направление этого изменения. При положительном коэффициенте регрессии с ростом значений Х растет и Y, при отрицательном – увеличение значений Х сопровождается уменьшением Y.
. Коэффициент b1 называют коэффициентом регрессии. Он характеризует наклон прямой к оси абсцисс и равняется тангенсу угла наклона j (рис.1). Согласно (2.6) b1 показывает, насколько в среднем изменится Y при изменении Х на одну единицу. Знак b1 определяет направление этого изменения. При положительном коэффициенте регрессии с ростом значений Х растет и Y, при отрицательном – увеличение значений Х сопровождается уменьшением Y.
Параметры регрессии – не безразмерны: постоянная уравнения регрессии b0 имеет размерность переменной Y; размерность b1 представляет собой отношение размерности зависимой переменной к размерности объясняющей переменной.
Пример.
Компания регулярно помещает рекламу на один из своих товаров в местную газету и ежемесячно ведет записи о суммах денег, затраченных на рекламу, и поступлений от продажи этого товара.
Если реклама эффективна, то можно предположить, что существует какая-то связь между затратами на рекламу и соответствующими ежемесячными объемами продаж: пусть с ростом суммы затраченных на рекламу средств растет объем продаж (по крайней мере в определенных пределах). Не существует теоретической основы, опираясь на которую мы могли бы написать уравнение, точно характеризующее связь продаж с расходами на рекламу. Имеется ряд факторов, неразрывно связанных между собой, которые определяют ежемесячный объем реализаций – это цена товара, цена товара-конкурента, период времени, погодные условия и т.д. Тем не менее, если расходы на рекламу являлись бы главным фактором, влияющим на продажу, то знание связи между этими двумя переменными было бы очень полезным для оценки объема продаж и соответствующего планирования финансовой политики компании.
Поскольку объем продаж – величина, которую желательно предсказать, то это будет зависимая переменная Y, тогда расходы на рекламу – независимая переменная Х.
Теперь необходимо проверить наши предположения о наличии и характере связи между переменными. Для этого воспользуемся собранными компанией ежемесячными данными об изменении рассматриваемых показателей (табл. 2).
Таблица 2
| Объем продажи товара, тыс. грн. | Затраты на рекламу, грн. |
Нам нужно объяснить изменение объема продаж (У), принимая затраты на рекламу в качестве независимой переменной (Х). Представим данные таблицы 1на графике, чтобы определить связь, которая существует между переменными (рис. 2).
 У, тыс.грн.
У, тыс.грн.









 50
50
 |

 40
40
 |


 30
30
 |
 20
20
 |


 10
10
 |
0 80 100 120 140 160 180 190 Х, грн.
Рисунок 2. Диаграмма рассеяния объема продаж в
зависимости от затрат на рекламу
Из рисунка 2 следует, что с увеличением затрат на рекламу количество продаваемого продукта растет. Расположение точек позволяет представить связь между рассматриваемыми показателями в виде прямой линии.
После получения численных оценок параметров по уравнению регрессии для каждого значения независимой переменной Хi может быть вычислено значение 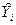 . Значения функции регрессии
. Значения функции регрессии 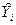 (i =1,2,…,n) называются расчетными или предсказанными значениями переменной Y для фиксированных Хi.
(i =1,2,…,n) называются расчетными или предсказанными значениями переменной Y для фиксированных Хi.
При линейной функции совокупность расчетных значений образует прямую регрессии. Как уже упоминалось, из-за искажающего влияния посторонних факторов-причин для каждого значения Хi может наблюдаться несколько эмпирических значений Yi , т.е. каждому значению Хi соответствует в статистическом смысле распределение вероятностей значений переменной Y. Значения функции регрессии 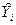 являются, таким образом, оценками средних значений переменной Y для каждого фиксированного значения переменной Хi.
являются, таким образом, оценками средних значений переменной Y для каждого фиксированного значения переменной Хi.
Отсюда становится очевидной экономическая интерпретация 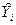 . Значения регрессии
. Значения регрессии 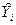 указывают среднее значение зависимой переменной Y при заданном значении Хi объясняющей переменной Х в предположении, что единственной причиной изменения переменной Y является переменная Х, а случайная возмущающая переменная e приняла нулевой значение. Разброс наблюдаемых значений переменной Y вокруг
указывают среднее значение зависимой переменной Y при заданном значении Хi объясняющей переменной Х в предположении, что единственной причиной изменения переменной Y является переменная Х, а случайная возмущающая переменная e приняла нулевой значение. Разброс наблюдаемых значений переменной Y вокруг 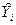 обусловлен влиянием множества причин, не поддающихся строгому учету и контролю. Разность между эмпирическим значением Yi и расчетным значением
обусловлен влиянием множества причин, не поддающихся строгому учету и контролю. Разность между эмпирическим значением Yi и расчетным значением 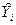 , называемая также остатком, дает численную оценку значения возмущающей переменной (возмущения) e; остатки обозначим как е.
, называемая также остатком, дает численную оценку значения возмущающей переменной (возмущения) e; остатки обозначим как е.
Таким образом, мы подошли к проблеме оценивания неизвестных параметров регрессии b0 и b1. Различным значениям их оценок b0 и b1 будут соответствовать различные линии. Из бесчисленного множества прямых, которые можно провести на плоскости, следует выбрать одну, наилучшим образом приближающуюся к опытным данным.
