ГЛАВА 7. Математическое моделирование в биологии и медицине

Модель Вольтерра

Математическое моделирование биологических процессов началось с создания первых простейших моделей экологической системы.

Рассмотрим модель хищник-жертва, предложенную итальянским математиком Вольтерра.

Допустим, в некотором замкнутом районе живут рыси и зайцы. Рыси питаются только зайцами , а зайцы - растительной пищей, имеющейся в неограниченном количестве. Необходимо найти макроскопические характеристики, описывающие популяции. Такими характеристиками являются число особей в популяциях - число зайцев N₁ и число рысей N₂.

Запишем дифференциальные уравнения, описывающие процесс изменения числа особей во времени.

При отсутствии рысей, изменение числа зайцев будет:

dN1=aN1dt

a - коэффициент, характеризующий размножение зайцев (жертв).

При отсутствии зайцев, изменение числа рысей будет:

dN2=-bN2dt

b - коэффициент, характеризующий вымирание рысей (хищников).

При совместном существовании зайцев и рысей:

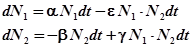
e - коэффициент, характеризующий убыль зайцев, вследствие их встреч с рысями.

g - коэффициент, характеризующий прирост рысей, вследствие их встреч с зайцами.

Скорость изменения популяций

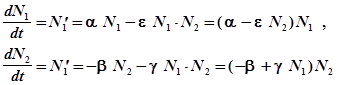(1)

Т.е. имеем систему нелинейных дифференциальных уравнений.

В стационарном состоянии, когда не изменяется численность зайцев и рысей имеем:

N₁=const и N₂=const и, следовательно,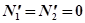

Т.е.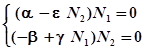

Решение этих уравнений (особые точки):

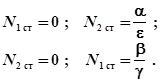(2)

Отсюда следует вывод:

Стационарные состояния не зависят от численности популяции, а определяются только коэффициентами прироста и потерь для другого вида.

Для определения устойчивости в стационарных состояниях необходимо исследовать систему вблизи этих состояний.

Допустим, возникли некоторые случайные отклонения, флуктуации n₁ и n₂. Определим поведение системы.

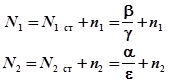
Возьмем производные. С учетом того, что производная от стационарного состояния равна 0, получим:

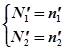
Подставим в (1)

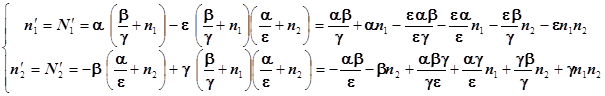(4)

Проделаем следующее:

Раскроем скобки, приведем подобные члены и пренебрежем членами en₁n₂ и gn₁n₂ вследствие их предполагаемой малости. Результатом пренебрежения ими будет линеаризация уравнений. В результате преобразования (4) получим:

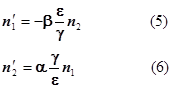
Найдем вторую производную:

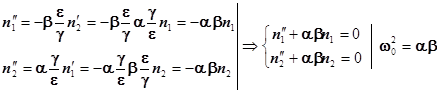
Окончательно получаем систему линейных дифференциальных уравнений второго порядка типа 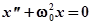, описывающих консервативную колебательную систему, (т.е. идеализированную систему, в которой запас энергии в процессе колебаний остается постоянным):

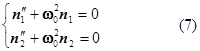
Найдем решение первого уравнения из системы (7). Напишем характеристическое уравнение:

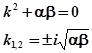
Зададим начальные условия:

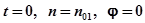, тогда: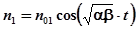

Чтобы найти функцию n₂, которая связана с функцией n₁, воспользуемся уравнением (5)

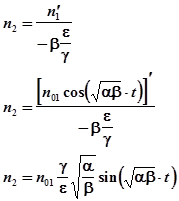
Окончательно получаем решение системы двух дифференциальных уравнений:

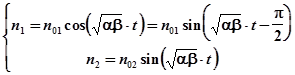
где n₀₁,n₀₂ - амплитудные значения флуктуаций,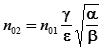

Таким образом, получаем:

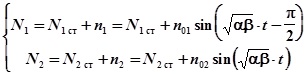
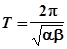- период колебаний, 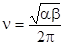- частота колебаний, 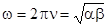- круговая частота.

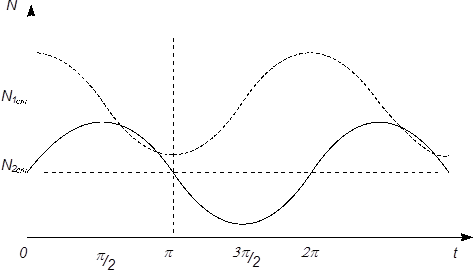
Рис.11. Зависимость изменения популяций от времени

Вывод. Популяции жертв и хищников испытывают периодические колебания одинаковой частоты, смещенные по фазе (причем максимум численности жертв всегда опережает максимум численности хищников).

Рассмотрим график зависимости N₁ от N₂, т.е. избавимся от t.

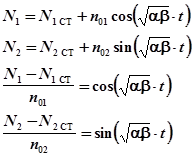
Произведя несложные математические преобразования, мы получили уравнение эллипса, с координатами центра (N_1ст,N_2ст).

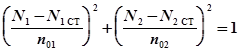
При n₀₁=n₀₂=n уравнение эллипса превращается в уравнение окружности с радиусом n.

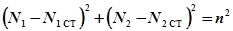
Итак, график зависимости N₂(N₁) представляет собой результат сложения двух колебаний одинаковой частоты, но с разными амплитудами и фазы которых отличаются на p/2.

Но, совершенно очевидно, что упрощенное решение(8) нашей системы дифференциальных уравнений (4) путем избавления от элементов 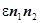и 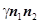привело нас к тому, что модель пришлось слишком идеализировать, что плохо соответствует реальной модели.

Сделаем попытку решить систему дифференциальных уравнений (1) другим методом. Разделим одно уравнение на другое, тогда получим

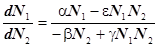или, перемножив, получим выражение

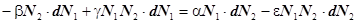
Разделим переменные, поделив правую и левую части уравнения на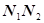

Проинтегрируем

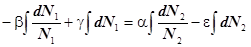
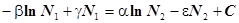
Преобразуем полученное выражение

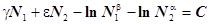или

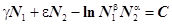
Итак, мы получили выражение, связывающее две переменные 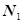и 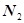, т.е. зависимость 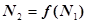в неявном виде. Начертим график этой функции

Полученная замкнутая кривая не является эллипсом, хотя отдаленно и напоминает эллипс, который получается при сложении колебаний одинаковой частоты и произвольной фазы.

Однако и здесь имеют место следующие закономерности:

1.Колебания численности популяци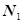й и 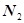, действительно имеют место.

2.Частоты этих колебаний весьма близки.

3.Сдвиг по фазе, хотя и не равен 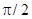, однако он явно наблюдается.