Моделирование цифровых устройств
В программе МС9имеется возможность моделирования цифровых и смешанных аналого-цифровых цепей. Обычно смешанные цепи моделируются в режиме временного анализа, однако другие режимы анализа также доступны. В режиме ACцифровые компоненты не участвуют в анализе частотных характеристик. В режиме DCзадержки сигналов в цифровых блоках игнорируются и рассчитываются логические уровни выходов цифровых устройств в стационарном режиме.
Цифровые компоненты в программе МС9 представлены в виде моделей, отражающих их правило функционирования на логическом уровне. Кроме этого, при подсоединении ко входу или выходу цифрового компонента аналоговых цепей, автоматически включается аналогово-цифровой или цифро-аналоговый интерфейсы, учитывающие параметры входных и выходных каскадов цифровых устройств. Устройства интерфейсов выполняют две функции. Во-первых, с их помощью при моделировании задаются схемы замещения входных и выходных каскадов цифровых компонентов. Во-вторых они обеспечивают преобразование электрических напряжений в логические уровни и наоборот при проведении моделирования смешанных цепей.
Все цифровые компоненты содержат параметр MNTYMXDLY, значение времени задержки распространения сигнала:
0 — значение задержки заданное по умолчанию;
1 — минимальное значение задержки;
2 — типичное значение задержки;
3 — максимальное значение задержки;
4 — расчет наихудшего случая.
Логические уровни цифровых узлов могут принимать одно из пяти значений:
1 — высокий уровень;
0 — низкий уровень;
R — положительный фронт (Raise, переход из состояния 0 в 1);
F — отрицательный фронт (Fall, переход из состояния 1 в 0);
X — неопределенное состояние.
Приведем несколько примеров моделирования цифровых устройств.
Пример.
Рассмотрим работу устройства, состоящего из 4-разрядных АЦП и ЦАП и ряда аналоговых компонентов (рисунок 5.36). На вход In аналого-цифрового преобразователя подается синусоидальный сигнал с генератора V2. Цифровой генератор U1 формирует периодическую последовательность прямоугольных импульсов, которые определяют частоту дискретизации и которые подаются на вход Convert. Питание АЦП и ЦАП осуществляется от источника V1 напряжением 10В. Разрядные выходы АЦП непосредственно соединены с одноименными входами ЦАП.
Результаты анализа в режиме Transient показаны на рисунке 5.37.
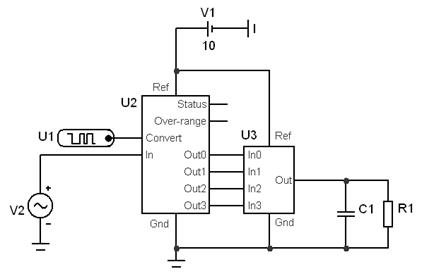
Рисунок 5.36 – Схема 4-разряднных АЦП и ЦАП
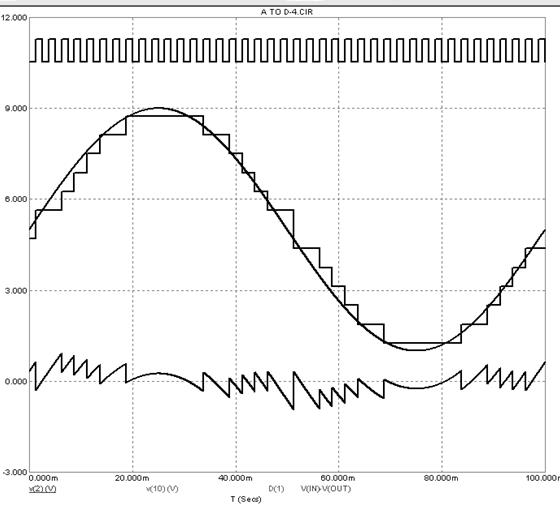
Рисунок 5.37 – Результаты временного анализа системы АЦП – ЦАП
На график выведены сигнал с частотой дискретизации, входной аналоговый сигнал АЦП и выходной ступенчатый сигнал ЦАП. В нижней части рисунка показан сигнал разности V(IN) – V(OUT) , определяющий ошибку аналого-цифрового преобразования.
Пример.
Рассмотрим построение и работу четырехразрядного двоичного суммирующего счетчика (рисунок 5.38).
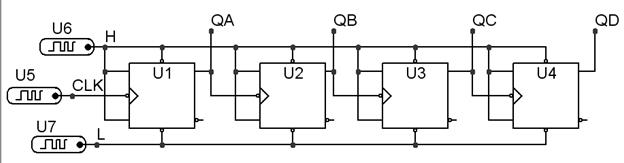
Рисунок 5.38 – Схема четырехразрядного двоичного суммирующего счетчика
Счетчик построен на четырех JK-триггерах U1-U4. Счетная последовательность импульсов формируется цифровым генератором U5. Генераторы U6 и U7 вырабатывают сигналы предварительной установки триггеров в состояние 1 (H) и 0 (L) , соответственно. Выходные двоичные разряды снимаются с выходов QA, QB, QC и QD.
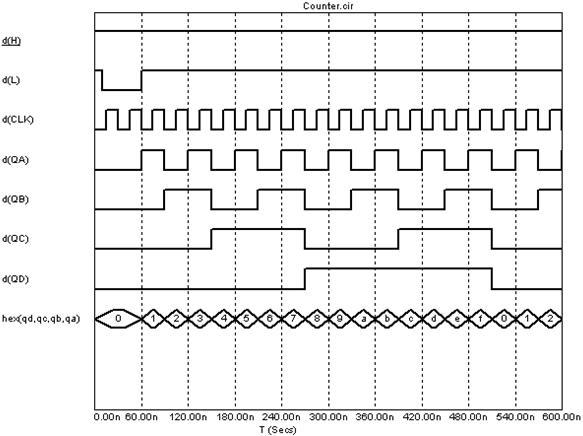
Рисунок 5.39 – Временные диаграммы работы счетчика
На рисунке 5.39 показаны результаты временного анализа работы счетчика. Видно, что состояние счетчика начинает изменяться только после снятия активного уровня со входа предустановки в состояние 0. Здесь же показаны значения состояний разрядных выходов счетчика в шестнадцатеричной системе счисления. Для этого в окне задания параметров моделирования был записан оператор hex(QD,QC,QB,QA). Видно, что модуль счета равен 16, как и должно быть для четырехразрядного двоичного счетчика.
Пример.
Большое значение в современных системах связи с кодовым разделением каналов играют шумоподобные сигналы — сигналы, свойства которых весьма близки свойствам «белого» шума. Говоря о свойствах сигнала, имеют в виду автокорреляционную функцию, которая должна быть возможно более узкой, а ее боковые лепестки должны быть минимальными.
Одним из видов таких сигналов являются М-последовательности или последовательности максимальной длины. М-последовательности являются периодическими с периодом состоящим из N символов. Уровень боковых лепестков автокорреляционной функции не превышает величину 1/N. Единицы и нули в М-последовательности встречаются одинаково часто, поэтому такие последовательности иногда называют псевдослучайными.
Формируются М-последовательности с помощью линейных схем на основе сдвигающих регистров и сумматоров по mod 2. Триггеры регистра сдвига подключаемые к сумматору определяются т.н. «характеристическим многочленом». Если в регистре K разрядов, то период М-последовательности равен:
N = 2K – 1 .
Для примера, построим автомат формирования М-последовательности с K = 4 и N = 24 – 1 = 15 (рисунок 5.40).
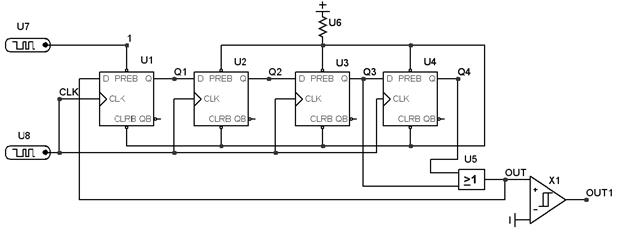
Рисунок 5.40 – Схема формирования М-последовательности с K = 4, N = 15
Регистр сдвига построен на четырех D-триггерах U1 – U4. Цифровой генератор U7 инициализирует регистр сдвига, устанавливая триггер U1 в начальное состояние «1», на остальные входы предустановки триггеров подается неактивный сигнал от источника логического сигнала U6. Генератор U8 формирует сигналы синхронизации для сдвига информации по регистру. Логический элемент U5 выполняет роль сумматора по mod 2. Компаратор Х1 преобразовывает цифровой сигнал OUT, принимающий логические значения 1 или 0, в аналоговый сигнал OUT1, который принимает значения 1В или -1В.
На рисунке 5.41 показаны временные диаграммы сигналов в разных узлах устройства. Отдельно на рисунке выделен диапазон 30mS , равный периоду повторения М-последовательности.
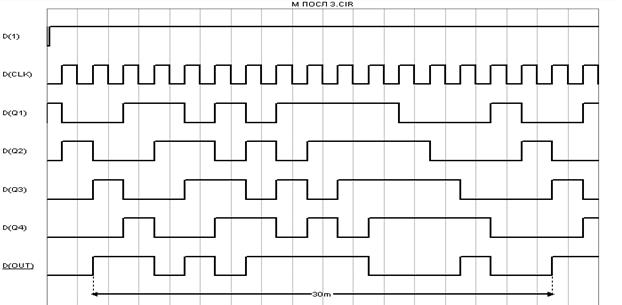
Рисунок 5.41 – Результаты моделирования формирователя
М-последовательности
На рисунке 5.42 приведена нормированная относительно максимального значения периодическая автокорреляционная функция сигнала OUT1, которая рассчитывается с помощью встроенного оператора AC(V(OUT1)).
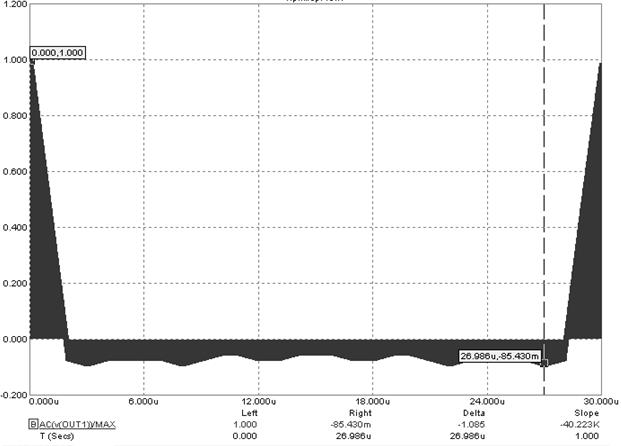
Рисунок 4.42 – Автокорреляционная функция М-последовательности N = 15
Здесь же выведены метки в точки максимального и минимального значений автокорреляционной функции. подтверждающая свойства. Из графика видно, что автокорреляционная функция М-после-довательности сосредоточена в узком диапазоне длительностью 2мкС, равном длительности одного элементарного импульса — чипа. Уровень боковых лепестков автокорреляционной функции данной М-после-довательности не превышает величины 1/0.085 ≈ 14.
На рисунке 5.43 для иллюстрации показаны форма сигнала, модулированного по фазе описанной М-последовательностью, и его спектр, а также спектр простого ФМ сигнала. Хорошо видно, что спектр сложного сигнала существенно расширяется, по сравнению с простым.
Все эти результаты очень хорошо согласуются с теоретическими исследованиями, что лишний раз подтверждает правильность заложенных в программу MC9 алгоритмов расчета и полезность ее для исследования различных электронных устройств.
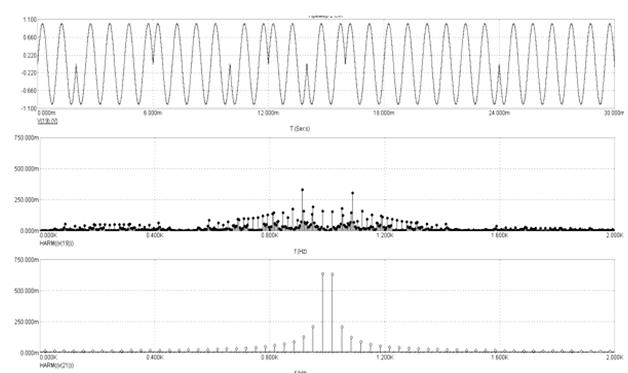
Рисунок 5.43 – Форма и спектры шумоподобного и простого сигналов
