Для системы нелинейных уравнений

,

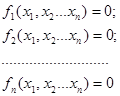представленных в виде неявных функций (см. уравнения (4) и (6) из раздела 2.3.1 а также приведенное ниже выражение (1)), следует предварительно найти выражения частных производных от всех n уравнений по всем неизвестным 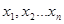, продифференцировав указанные функции по всем переменным. Система линейных алгебраических уравнений относительно попра-

Система n нелинейных алгебраических уравнений относительно неизвестных х₁, х₂,… х_n

В развернутом виде При решении узловых уравнений В матричной форме записи:

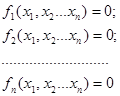
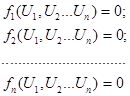
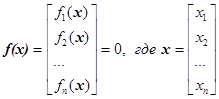(1)

Система линейных алгебраических уравнений относительно поправок к неизвестным

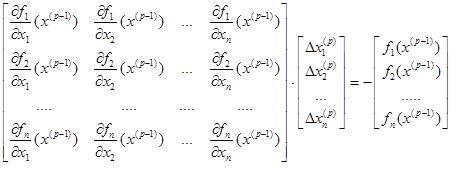
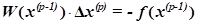(2)

Значения неизвестных на р-м шаге итерационного процесса

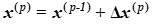(3)

вок к неизвестным в матричной форме имеет вид (2). Матрица коэффициентов этой системы — значений частных производных от всех уравнений по всем неизвестным 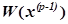называется матрицей Якоби.

Алгоритм расчета:

1. Задаются точностью расчета ԑ и значениями неизвестных на нулевом шаге итераций. Поскольку номер шага итераций р принимает значения р=1, 2, 3…, значения неизвестных на нулевом шаге можно записать, как значения неизвестных на р-1 –ом шаге, когда р =1— .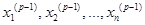

2. Вычисляют значения функций при этих значениях неизвестных 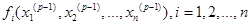т.е. невязки, и сравнивают их с заданной точностью: 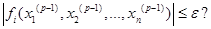. Если точность достигнута — конец расчета, если не достигнута — идти к п.3.

3. В предварительно полученные выражения для частных производных подставляются значения неизвестных на нулевом (в общем случае на p-1- ом шаге итераций 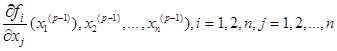) и рассчитывают значения элементов матрицы Якоби, завершая формирование системы линейных алгебраических уравнений (2) относительно поправок к неизвестным.

4. Система линейных алгебраических уравнений (2) относительно поправок к неизвестным решается, как правило, методом Гаусса, находятся значения поправок к неизвестным 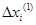(в общем случае на p- ом шаге итераций 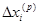) и значения неизвестных на первом 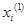(в общем случае на р-м 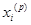) шаге итерационного процесса согласно (3).

5. .

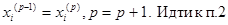Метод Ньютона обеспечивает быструю сходимость, и первое приближение дает удовлетворительный для практики результат. Обычно требуется от 2 до 8 итерации, независимо от порядка системы уравнений. Поэтому он получил широкое применение в отечественных и зарубежных программах для расчета установившихся режимов. Требует он памяти ЭВМ столько, сколько и метод Гаусса, т.е. больше, чем метод Зейделя.

Недостатки метода Ньютона:

1) Метод чувствителен к значениям неизвестных, которыми задаются на нулевом шаге итераций. При расчете установившихся режимов в электрических системах часть искомых неизвестных может быть задана с относительно большой точностью. Такими неизвестными могут быть модули узловых напряжений, которые не могут значительно отличаться от номинальных напряжений соответствующих участков сети.

2) На каждой итерации приходится заново вычислять значения элементов матрицы Якоби, находя значения частных производных при значениях переменных, найденных на предыдущей итерации.

3) Уравнения, определяющие режим системы, не могут дифференцироваться в комплексной форме, поэтому для применения метода Ньютона, требующего вычисления частных производных, система уравнений должна быть преобразована в систему уравнений с действительными коэффициентами и неизвестными.

2.4.5 Система нелинейных уравнения узловых напряжений в форме баланса мощностей с действительными коэффициентами и неизвестными в полярной системе координат

Выше (см. п. 2.3.1) получено выражение для системы уравнений узловых напряжений в форме баланса мощностей, в которой коэффициенты и неизвестные – комплексные числа.

Перепишем нелинейное уравнение узловых напряжений в форме баланса мощностей (6) из раздела 2.3.1., полученное для i-го узла, изменив знаки у всех слагаемых этого уравнения на противоположные, и представив его как некоторую функцию небаланса мощностей в i-м узле.

.

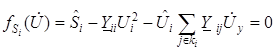Если бы были известны точные значения неизвестных напряжений, как результат решения системы узловых уравнений, то после подстановки их в это уравнение был бы получен 0, если точные значения 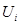не известны, то после подстановки любых приближенных значений получим невязку (небаланс) мощностей в i-м узле. По этой причине уравнение (6) записывается как функция небаланса мощностей в i-м узле 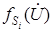, зависящая от неизвестных напряжений.

Представим комплексы величин, которые входят в это уравнение, через их действительные и мнимые части. Мощности

.

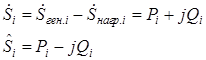Проводимости

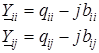- собственные и взаимные проводимости i-го узла.

В отличие от принимаемого ранее определения напряжений в узлах в прямоугольной системе координат 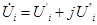перейдем к полярной системе координат:

.

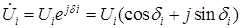Здесь:

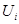- модуль напряжения в i – ом узле;

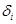- фазовый угол напряжения i – го узла между положительным направлением вектора напряжения этого узла и положительным направлением действительной оси комплексной плоскости.

Аналогично:

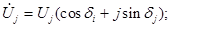
Модули 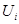и фазовые углы 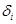являются неизвестными х при решении узловых уравнений. Подставив указанные комплексные величины в выражение для 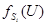,после преобразований, приравняв отдельно действительные и мнимые части комплексов, получим выражения для функций небалансов активных и реактивных мощностей

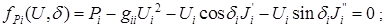(1)

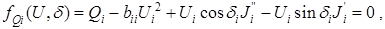
где: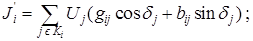

Здесь все 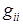, 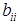со знаком +, все 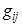, 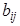со знаком -..

Система уравнений (1), в которой неизвестные находятся под знаком тригонометрических функции, называется системой тригонометрических уравнений узловых напряжений в форме баланса мощностей.