Поняття, приклади і найпростіші властивості векторного простору

У різних розділах математики лінійні операції виконуються не тільки над векторами, а й над різними іншими об’єктами: матрицями, функціями, многочленами, тощо. Можливість підходити до цих об’єктів із загальної точки зору дає поняття векторного (лінійного) простору.

Нехай 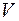– непорожня множина елементів будь-якої природи, які будемо позначати 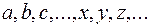і нехай 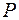– числова множина дійсних або комплексних чисел, елементи якої будемо позначати 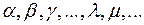. Визначимо в множині 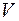операцію додавання елементів: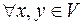 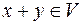і операцію множення елемента на число: .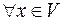

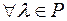
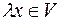Означення. Множина 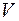називається лінійним (векторним) простором, якщо в 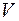визначені алгебраїчна операція додавання і операція множення на числа з фіксованої числової множини 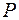, причому виконані наступні умови (аксіоми векторного простору):

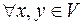
1. 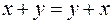комутативність додавання ;

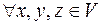
2. 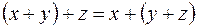–асоціативність додавання;

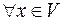
3. 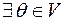: 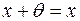- існування нульового елемента ;

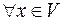
4. 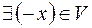: 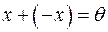- існування протилежного елемента;

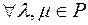
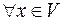
5. 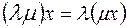– асоціативність множення на число ;

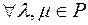
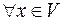
6. 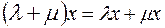- дистрибутивність відносно додавання чисел ;

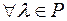
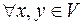
7. 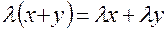- дистрибутивність відносно додавання елементів;

8. .

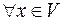
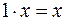Елементи лінійного простору називаються векторами, елемент 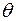називаєтьсянульовим вектором (нуль-вектором).

Приклади лінійних просторів:

1) Множина 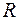дійсних чисел із звичайними операціями додавання і множення є дійсним векторним простором. Множина 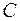комплексних чисел відносно операцій додавання комплексних чисел і множення комплексних чисел на дійсні числа є дійсний векторний простір .

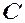2) 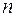-вимірний арифметичний простір 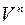є векторним простором.

3) Сукупність 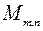всіх матриць розмірності 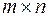з дійсними елементами утворює дійсний векторний простір відносно операцій додавання матриць і множення матриць на число.

4) Множина всіх геометричних векторів звичайного тривимірного простору з початком в точці 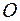відносно операцій додавання векторів і множення векторів на число утворює дійсний векторний простір .

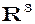Множина всіх векторів деякої площини і деякої прямої відносно операцій додавання векторів і множення векторів на число також є дійсними векторними просторами. Позначимо їх відповідно 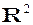і .

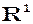5) Сукупність всіх многочленів від змінної 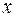з дійсними коефіцієнтами відносно операцій додавання многочленів і множення многочленів на число утворює дійсний векторний простір.

6) Сукупність всіх неперервних функцій дійсної змінної, які визначені на деякому відрізку 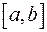, утворює дійсний векторний простір відносно операцій додавання функцій і множення функцій на число. Роль нуль-вектора відіграє функція, яка тотожно дорівнює нулю.

З означення безпосередньо випливають наступні

Найпростіші властивості лінійного простору:

1) Єдиність нульового вектора. В векторному просторі 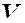існує єдиний нульовий вектор, тобто такий, що 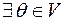: 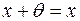. (аксіома 3)

2) Єдиність протилежного елемента. В векторному просторі 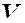для будь-якого вектора 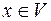існує єдиний вектор 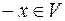такий, що 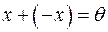. (аксіома 4)

3) Для будь-якого вектора .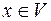

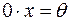4) Для будь-якого числа 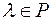і Î .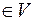

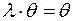5) Якщо добуток 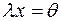Î, то 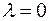або , або .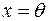

6) Для будь-якого вектора 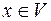елемент 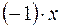є протилежним до .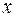