Основные понятия математической статистики

Будем считать, что опыт состоит из бесконечного множества испытаний, перенумерованных числами 1, 2, 3,... В каждом испытании измеряется значение случайной величины X. Таким образом, с опытом связана последовательность случайных величин X₁, X₂,...: значение случайной величины X_k в результате опыта равно значению, которое принимает случайная величина X в k-м испытании данного опыта.

Случайная величина

M_n ( X ) = ( X₁ + X₂ +...+ X_n ) / n

называется выборочным средним, а случайная величина

D_n ( X ) = (( X₁ - M_n ( X ))² + ( X₂ - M_n ( X ))² +...+ ( X_n - M_n ( X ))² ) / ( n – 1 )

называется несмещённой оценкой дисперсии случайной величины X (оценка числовой характеристики случайной величины считается несмещённой в том случае, когда её математическое ожидание совпадает с точным значением соответствующей числовой характеристики случайной величины X). В учебниках по математической статистике приводятся формулы для вычисления несмещённых оценок различных числовых характеристик случайной величины.

Пусть a – точное значение числовой характеристики случайной величины X, A_n - её несмещённая оценка, ε – положительное число, 0 < α < 1. Число 2 ε называется длиной доверительного интервала несмещённой оценки A_n числовой характеристики случайной величины соответствующего доверительной вероятности α, если вероятность того, что - ε ≤ A_n – a < ε равна α. Когда серединой доверительного интервала считают оценку A_n, число α равно вероятности того, что интервал ] A_n – ε, A_n + ε ] накрывает число a, если же серединой доверительного интервала считать точное значение a, то α равно вероятности того, что несмещённая оценка A_n попадает в интервал [ a – ε, a + ε [.

Будем предполагать, что случайные величины X₁, X₂,..., X_n взаимно независимы и имеют ту же функцию распределения, что и случайная величина X. В силу центральной предельной теоремы выборочное среднее ( X₁ + X₂ +...+ X_n ) / n можно заменить случайной величиной N, распределённой по нормальному закону с параметрами ( m, σ n^-1/2 ), где m – математическое ожидание случайной величины X, σ – её квадратичное отклонение. Неравенства - ε ≤ N – m < ε и

( - ε ) / ( σ n^-1/2 ) ≤ ( N – m ) / ( σ n^-1/2 ) < ε / ( σ n^-1/2 )

эквивалентны, следовательно,

p ( - ε ≤ N – m < ε ) = p ( - ε / ( σ n^-1/2 ) ≤ ( N – m ) / ( σ n^-1/2 ) < ε / ( σ n^-1/2 )) = p (( N – m ) / ( σ n^-1/2 ) < ε / ( σ n^-1/2 ) ) - p (( N – m ) / ( σ n^-1/2 ) < - ε / ( σ n^-1/2 )).

Случайная величина ( N – m ) / ( σ n^-1/2 ) распределена по нормальному закону с параметрами ( 0, 1 ), поэтому

уменьшаемое и вычитаемое в правой части равенства выражаются в виде определённых интегралов функции

exp ( - t² / 2) / ( 2 π )^½,

пределами интегрирования в первом интеграле служат точки - ∞ и ε / ( σ n^-1/2), а во втором - точки - ∞ и - ε / ( σ n^-1/2 ). Отсюда вытекает, что

p ( - ε ≤ N – m < ε ) = ( 2 π )^-½ 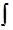_{[ - s, s ]} exp ( - t² / 2) dt

где s = ε / ( σ n^-1/2 ) = ε n^1/2 / σ.

Функция

erf ( z ) = 2 π-½ 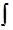_{[ 0, z ]} exp ( - t² ) dt

называется функцией ошибок ( error function ). Таким образом,

p ( - ε ≤ ( X₁ + X₂ +...+ X_n ) / n – m < ε ) = erf ( ε ( n / 2 )^1/2 / σ ).

Задание. Докажите, что

p ( - ε ≤ ( X₁ + X₂ +...+ X_n ) / n – m < ε ) = erf ( ε ( n / 2 )^1/2 / σ ).