Ндивидуальные задания студентам группы СВ-312

№№	Ориентиры	По	До мили	СКП По	СКП До	Счислимые координаты
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(20)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(21)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(22)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(23)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(24)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(25)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(26)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(27)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(28)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(29)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(30)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(31)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(32)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(33)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(34)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(35)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(36)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(37)	Маяк Меганом				±1,5	λ = 36°00,0ʼΕ
	Маяк Кыз-Аул			±1,5		φ =44°00,0ʼΝ
(38)						λ = 36°00,0ʼΕ

ндивидуальные задания студентам группы СВ-32

№№	Ориентиры	По	До мили	СКП По	СКП До	Счислимые координаты
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(39)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(40)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(41)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(42)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(43)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(44)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(45)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(46)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(47)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(48)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(49)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
(50)	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
	Мыс Аю-Даг				±1,5	λ = 35°00,0ʼΕ
	Маяк Меганом			±2,0		φ =44°00,0ʼΝ
	Мыс Аю-Даг				±1,5	φ =44°00,0ʼΝ
	Маяк Меганом			±2,0		λ = 35°00,0ʼΕ
	Мыс Аю-Даг				±1,5	φ =44°00,0ʼΝ
						λ = 35°00,0ʼΕ

Методические указания

Ответы на выполнение задачи № 4 должны содержать следующие результаты решения своего варианта задачи ОМС по измерению двух навигационных параметров.

рафически

1.1 Сняли с карты в точке пересечения По и Dо

φ₀ =44°… , ..ʼΝ

λ₀ = 37°… , ..ʼΕС = ……°……. , …ʼ

1.2 Сместив изолинии на величины СКП П_о и СКП Д_о в полученную фигуру погрешности вписывают эллипс и снимают его элементы: а=… ,… ʼ, в=…. , …ʼ , β₀=……..°.

рафоаналитически

2.1 Рассчитывают по формулам плоской и сферической тригонометрии счислимые значения пеленгов и дистанций, используя координаты ориентиров и счислимой точки.

Для контроля снимают с карты между ориентирами и счислимой точкой величины:

Пс₁ = , Dс₁ = , Пс₂= , Dс₂ =

.

2.2 Рассчитывают градиенты изолиний:

g_П = 57,3°/ Dс₁ = g_D = 1

и направления градиентов:

τ_П = Пс₁ + 90°; τ_D = Пс₂.

2.3 Рассчитывают элементы переносов линий положения (ЛП) по формулам:

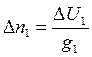= (По-Пс₁)/g _{П = ;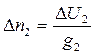} = (Dо-Dс₂)/g_D=

2.3 На уарте от счислимой точки по элементам t₁, Dn ₁и Dt₂, n₂ строят линии положення и в точке их пересечения снимают обсервованные координаты места судна j₀ и l₀.

2.5 Построить на обратной стороне бланка астрономических вычислений по направлениям градиентов и величинам переносов две ЛП и вычислить в правом нижнем углу листа величины обсервованных координат:

На бланке от счислимой точки по элементам t₁, Dn ₁и Dt₂, n₂ строят линии положення I–I и II–II, в последующем порядке:

- Через центр бланка, принимаемый за счислимую точку по делениям на рамке проводится направление градиента t₁ первого навигационного параметра.

- Вдоль направления градиента откладывается перенос n₁ по направлению, если перенос положителен, в противоположном – если отрицателен.

- Через полученную точку жирным цветом проводится линия положения, обозначаемая с концов римской цифрой I.

- Для построения второй линии положения производятся действия 1-3.

- Пересечение линий положения даёт нам обсервованную точку с координатами.

j₀=j_с+Dj

l₀=l_с+Dl

2.6 Среднеквадратическую погрешность или смещение ЛП рассчитывают по формуле:

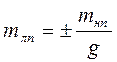, где: m_нп – СКП навигационного параметра,

g – его градиент. В нашем случае:

т_лп1=т_П/g _П = СКПП_о/g _П= ; т_лп2 ⁼ СКПД_о/g_D =

2.7 Радиальная СКП места судна рассчитывается по формулам:

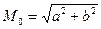
налитически

3.1 При аналитическом методе координаты места судна получают совместным решением системы уравнений ЛП:

, где

Dw- отшествие.

Решив эту систему методом определителей и учитывая, что

Dl=Dw/cos(j_c),

получим приращения координат:

,

где Q=t₂-t₁,

далее определяем обсервованные координаты:

j₀=j_с+Djl₀=l_с+Dl

3.2 Для строгого построения эллипса погрешностей рассматриваются векториальные ошибки , линии положения 1 и 2 по направлению ЛП₂ и ЛП₁.

Учитывая, что вектора - сопряжённые полуоси эллипса используют теорему Аполлония

или

;

Где a угол, определяющий направление большой полуоси эллипса, который всегда откладывается внутри острого угла Qот более точной ЛП.

3.3 Проверяют значение радиальной СКП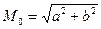

Задание № 5 Определение места судна по трем ЛП с оценкой точности.

Решить задачу ОМС и оценить точность полученного места судна.

3. Графически построить:

3.1 Изолинии по значениям навигационных параметров;

3.2 Обозначить фигуру погрешности линиями положения.

4. Графо-аналитическок решенеие:

2.1. рассчитать аналитически на плоскости и для контроля снять с карты счислимые Пс и Дс всех ориентиров;

2.2. рассчитать градиенты изолиний и их направления;

2.3 рассчитать элементы ЛП;

2.4 построением ЛП проверить исходную фигуру погрешностей;

2.5 рассчитать смещения и веса ЛП и с их учетом найти на карте вероятнейшее место судна штурманским приемом и центрографическим способом;

2.6 на карте построить полигон весов и рассчитать полуоси эллипса погрешностей;

2.7 определить и построить на карте радиальную СКП места судна с вероятностью 0,95.

3. Аналитически определить:

3.1 по координатам ориентиров и счислимого места судна рассчитать Пс и Дс:

3.2 рассчитать аналитически градиенты изолиний и их направления;

3.3 рассчитать элементы ЛП, построить их на бланке и составить их уравнения в отрезках координат;

3.4 рассчитать смещения и веса ЛП;

3.5 составить таблицу аналитической обработки исходной информации и заполнить её по данным уравнений ЛП;

3.6 составить нормальные уравнения ЛП и рассчитать обсервованные координаты;

3.7 рассчитать все элементы эллипса погрешностей, показать его на бланке;

3.8 рассчитать и построить на бланке радиальную СКП места судна;

3.9 сравнить результаты графоаналитического аналитического решения задачи.

Карта № 3227 для группы СВ-311и № 3104 для остальных групп. Задание для студентов по группам.