Трехкартинный комплексный чертеж и его основные свойства

Трехкартинный комплексный чертеж образуется методом ортогонального про­ецирования на три взаимно перпендикулярные плоскости проекций: /7, _L П₂ -L П₃ (рис. 5.6).

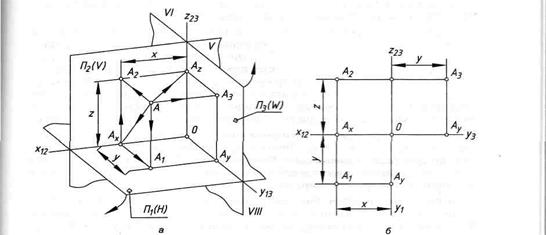Введением плоскости fl₃{W) мы разделили все пространство на восемь частей, каждая из которых называется октантом. Нумерация четвертей сохраняется за первыми четырьмя октантами, а новым октантам присваиваются номера с V по VIII, как показано на рис. 5.6, а, где октант VII не показан, так как его не видно.

Постоянная чертежа- диагональ.

Задачи 2 и 3.

4. Проецирование прямой

Прямая может иметь свои проекции в виде двух прямых или в виде точки и прямой.

Виды прямых:

	Общего положения		Горизонталь		Фронталь		Профильная прямая

Проф. Проец.

Фронт. Проец.

Гориз. Проец.

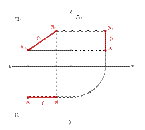
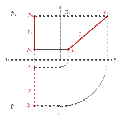
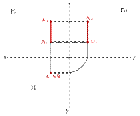
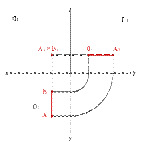
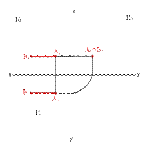
Определения:

1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения

2. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями

3. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями

4. Прямые параллельные профильной плоскости проекций называются профильными

5.

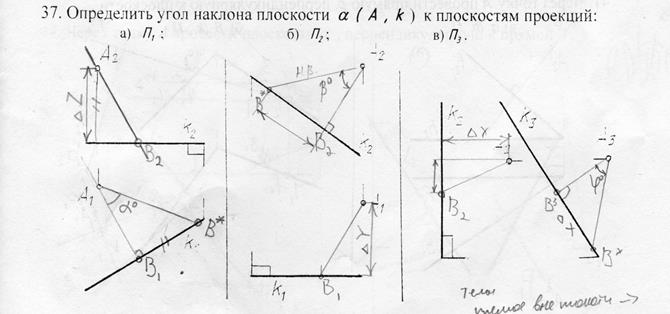
Определение длины отрезка прямой линии и углов наклона прямой к плоскостям проекций

(метод прямоугольного треугольника)

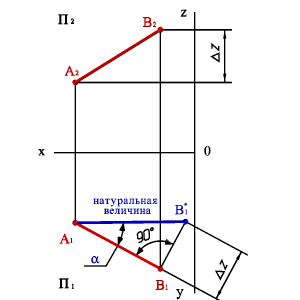
Длину отрезка АВ и a - угол наклона отрезка к плоскости П1 можно определить из прямоугольного треугольника АВС |AС|=|A1B1|, |BС|=DZ. Для этого на эпюре (рис.31) из точки B1 под углом 900 проводим отрезок |B1B1*|=DZ, полученный в результате построений отрезок A1B1* и будет натуральной величиной отрезка АВ, а угол B1A1B1*=a. Рассмотренный метод называется методом прямоугольного треугольника. Тот же результат можно получить при вращении треугольника АВС вокруг стороны AС до тех пор, пока он не станет параллелен плоскости П1, в этом случае треугольник проецируется на плоскость проекций без искажения.

Задание плоскости на чертеже

Через три точки А, В, С, не принадлежащие одной прямой, можно провести одну и только одну плоскость). Точки А, В и С составляют геометрическую часть определителя плоскости.

Классификация плоскостей

фронталь

профильная

горизонталь

фрон. Проец.

проф. Проец.

Гориз. Проец.

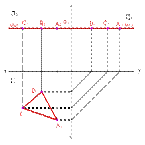
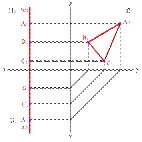
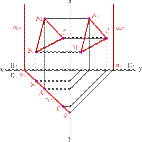
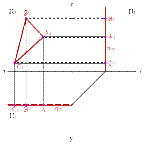
1. Плоскость, перпендикулярная горизонтальной плоскости проекций (a^П1), называется горизонтально проецирующей плоскостью

2. Плоскость, перпендикулярная фронтальной плоскости проекций (a^П2)- фронтально проецирующая плоскость.

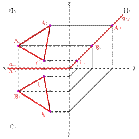
3. Плоскость, перпендикулярная профильной плоскости ( a^П3) - профильно проецирующая плоскость.

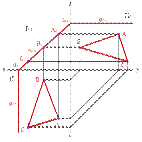
4. Горизонтальная плоскость - плоскость, параллельная горизонтальной плоскости проекций (a//П1) - (a^П2,a^П3)

5. Фронтальная плоскость - плоскость, параллельная фронтальной плоскости проекций (a//П2), (a^П1, a^П3)

6. Профильная плоскость - плоскость, параллельная профильной плоскости проекций (a//П3), (a^П1, a^П2)

7.