Решение задач линейного программирования с помощью надстройки

ПОИCК РЕШЕНИЯ в среде EXCEL

Поиск решения – это надстройка EXCEL, позволяющая реализовывать модели линейной, нелинейной и дискретной оптимизации. Если в меню Данные отсутствует команда Поиск решения, значит необходимо загрузить эту надстройку.

Решение оптимизационной задачи состоит из нескольких этапов:

Этап 1.

Построить математическую модель задачи: выбрать управляющие переменные 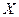, определить функцию цели и записать систему ограничений.

Этап 2.

Подготовить таблицу данных в EXCEL (рис 1).

• На листе Excel обозначить имеющиеся переменные 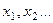: В1:Е1;
• Зарезервировать ячейки для их значений – изменяемые ячейки В2:Е2: эти ячейки пока оставим пустыми, по окончании решения в этих ячейках будут находится оптимальные значения управляющих переменных;

· Ввести в отдельные ячейки В5:Е5 коэффициенты целевой функции ;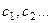

· Обозначить целевую функцию 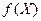: в ячейку F5 (целевая ячейка) ввести формулу для вычисления значения этой функции 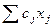со ссылкой на ячейки значений коэффициентов В5:Е5 и переменных В2:Е2.

• Для каждого из ограничений задачи заполнить ячейки с исходными данными: в ячейки В8:Е10 ввести коэффициенты левых частей неравенств 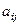; в ячейки Н8:Н10 ввести правые части ограничений 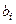; в ячейках G8:G10 указать знак неравенства (<=, >= или =);
• В ячейки F8:F10 ввести формулы для вычисления значений левых частей ограничений .

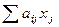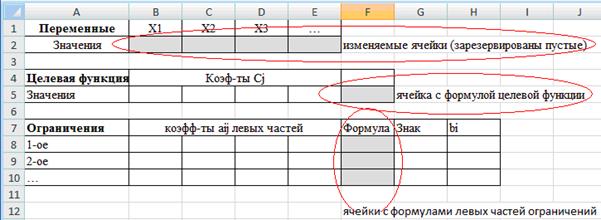
Рис. 1.

Для ввода формул 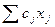, 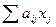удобно использовать мастер функций: 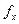/ математические / СУММПРОИЗВ.

Этап 3.

Для запуска Поиск решения выбрать команды Данные Поиск решения. После выбора команды Поиск решения появиться диалоговое окно Поиск решения (рис 2.). В нем есть три основных поля:

• Установить целевую ячейку;
• Изменяя ячейки;
• Ограничения;

Установить целевую ячейку – указывается ячейка, в которой находится формула для вычисления значения функции цели 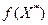- F5. Эта ячейка связана с другими ячейками с помощью формул. Здесь же выбирается направление оптимизации: наибольшее или наименьшее значение функции цели ищется в задаче.

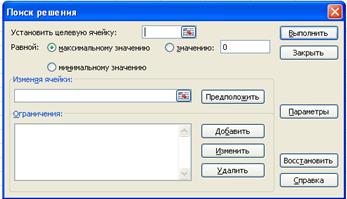
Рис. 2.

Изменяя ячейки - указываются зарезервированные изменяемые ячейки В2:Е2, соответствующие управляющим переменным в модели, значения в которых будут изменяться для достижения экстремума целевой функции. В этих ячейках в результате расчета будут находиться значения переменных оптимального плана 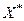. Для поиска решения можно указать до 200 изменяемых ячеек.

К этим ячейкам предъявляются два основных требования: они не должны содержать формул и должны влиять на значение целевой ячейки, т.е. их адреса должны использоваться в формуле, введенной в целевую ячейку.

Ограничения модели определяются с помощью значений соответствующих ячеек (рис 3). Структура ограничения, введенного в Поиске решения, полностью соответствует ограничению, построенному в модели: левая часть, знак, правая часть:

ссылка на ячейку – указываются ячейки, в которых введены формулы для вычисления левых частей неравенств системы ограничений F8:F10 (не путать с ячейками, содержащими коэффициенты левых частей ограничений В8:Е10). Ограничения могут налагаться как на целевую ячейку, так и на переменные (до 100 дополнительных ограничений);

тип каждого из ограничений модели ( 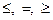) задается (вводится) в специальном окне диалога при выполнении команды;

ограничение - указываются ячейки, в которых введены правые части выражений в системе ограничений Н8:Н10.

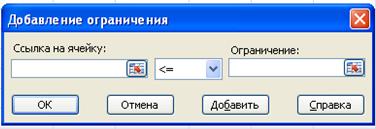
Рис3.

В режиме Параметры (Рис. 4) окна диалога Поиск решения задается тип модели (линейная или нелинейная) и прямые ограничения ( отмечаются галочками поля «Линейная модель» и «Неотрицательные значения»).

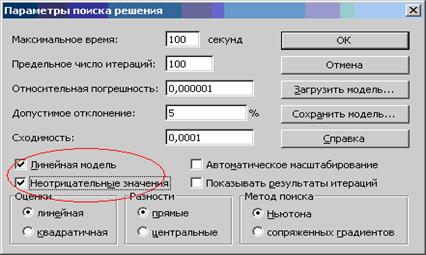
Рис. 4

Этап 4.

После команды Выполнить осуществляется поиск оптимального решения и в итоге появляется диалоговое окно Результат поиска решения (Рис. 5).

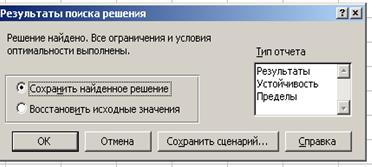
Рис. 5

В этом диалоговом окне содержатся сведения об итоговых сообщениях процедуры поиска решения. Например, в случае несовместности системы ограничений EXCELбудет выдавать сообщение Поиск не может найти подходящего решения. Если решение задачи отсутствует вследствие неограниченности целевой функции на множестве допустимых решений, то EXCEL будет выдавать сообщение Значения целевой ячейки не сходятся.

Необходимо проконтролировать успешное завершение решения задачи: появляется сообщение Решение найдено. Все ограничения и условия оптимальности выполнены.

Задача 1.

Найти оптимальный план 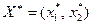выпуска двух видов смеси, обеспечивающий максимум прибыли, если прибыль от реализации 1 ед. каждого вида смеси составляет 31 и 42 ден.ед. На производство 1 ед. 1-й смеси расходуется 0,8 ед. ресурса Р1 и 0,4 ед. ресурса Р2; для второго вида смеси эти расходы составляют – 0,2 и 0,6, соответственно. Запасы ресурсов Р1 и Р2 составляют 37 и 24 ед., соответственно.

Решение.

Этап 1. Функция цели .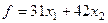

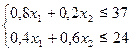
Ограничения

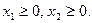
Этап 2.

1.Подготовим форму для ввода условий задачи (рис 6).

Зарезервированы ячейки:

В3:С3 – для оптимальных значений управляющих переменных 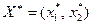,