Центральная предельная теорема

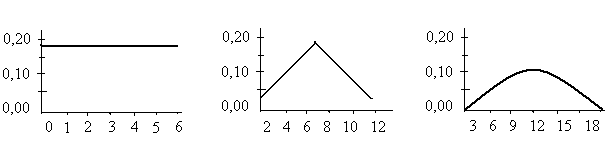
Рассмотрим распределение вероятностей суммы очков на игральных костях. На рисунках ниже приведены многоугольники распределения для случая одной, двух и трех костей.

Видно, что с увеличением числа костей многоугольник распределения все более становится похожим на график плотности нормального закона. Эта близость к нормальному закону становится еще более разительной при еще большем числе костей.

Оказывается, такая близость суммы большого числа случайных величин к нормальному закону распределения является закономерной и носит в теории вероятности название центральной предельной теоремы.

В грубой формулировке эта теорема выглядит так:

Сумма большого числа независимых случайных величин при довольно широких предположениях подчинена нормальному закону распределения.

Перейдем теперь к более точным формулировкам.

ОПРЕДЕЛЕНИЕ 1. Говорят, что последовательность независимых случайных величин Х₁,Х₂,...Х_n удовлетворяет условиям Ляпунова, если

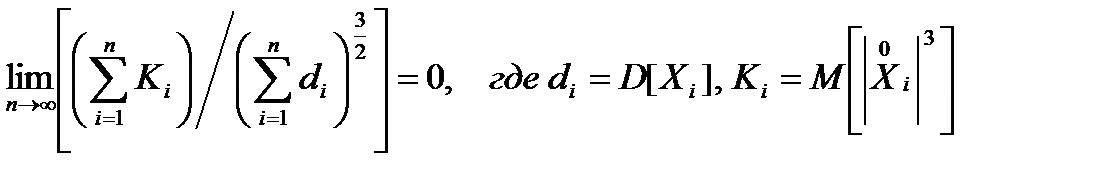
ЗАМЕЧАНИЕ. Рассмотрим один практически важный случай, когда независимые случайные величины имеют один и тот же закон распределения. Тогда

,

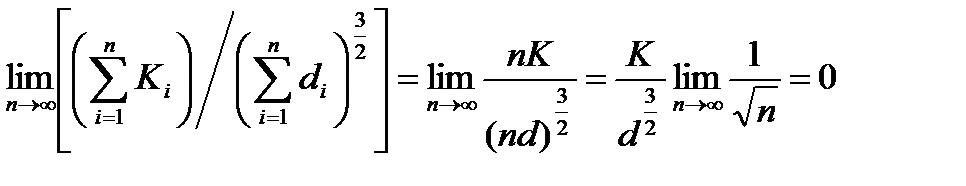т.е. условие Ляпунова в этом случае выполнено.

Смысл сделанного замечания заключается в том, что для выполнения условия Ляпунова все случайные величины должны иметь примерно одинаковое распределение, т.е. ни одна из них не должна резко выделяться среди остальных.

Дадим теперь точную формулировку центральной предельной теоремы, которую примем без доказательства.

ТЕОРЕМА. Если последовательность Х₁,Х₂,...Х_n независимых случайных величин удовлетворяет условию Ляпунова, то

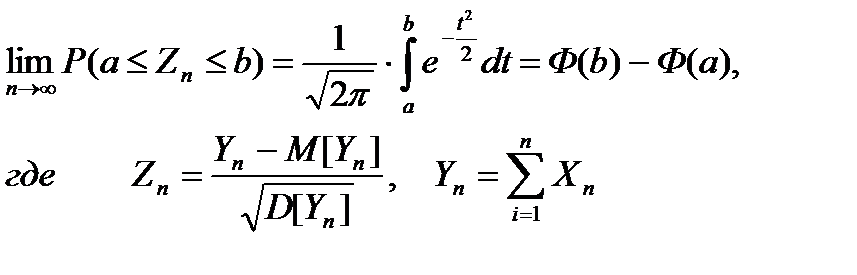
Эта теорема показывает, что на практике и в теории нормальное распределение играет особую, центральную роль, коль скоро речь идет о большом числе случайных величин, а на практике такая ситуация встречается достаточно часто.

ПРИМЕР 2. Завод выпускает валы турбогенераторов с номинальным диаметром D. Из-за множества складывающихся случайных влияний (температура, вибрация, неидеальная технология, неоднородность материала, ошибки измерений и т.д.) диаметр изготавливаемых валов D является случайной величиной. Если все факторы влияют примерно одинаково (условия Ляпунова), то - это нормально распределенная случайная величина.

Рассмотрим еще одно приложение центральной предельной теоремы, с которым мы уже сталкивались.

Рассмотрим схему Бернулли с числом «успехов» Х==Х₁ +Х₂ +...+Х_n Случайные величины X_i независимы и имеют один и тот же закон распределения (см.п.2.1). Вычислим вероятность того, что число успехов будет в пределах от k₁ до k₂ , когда число испытаний неограниченно возрастает. Применяя центральную предельную теорему, получаем

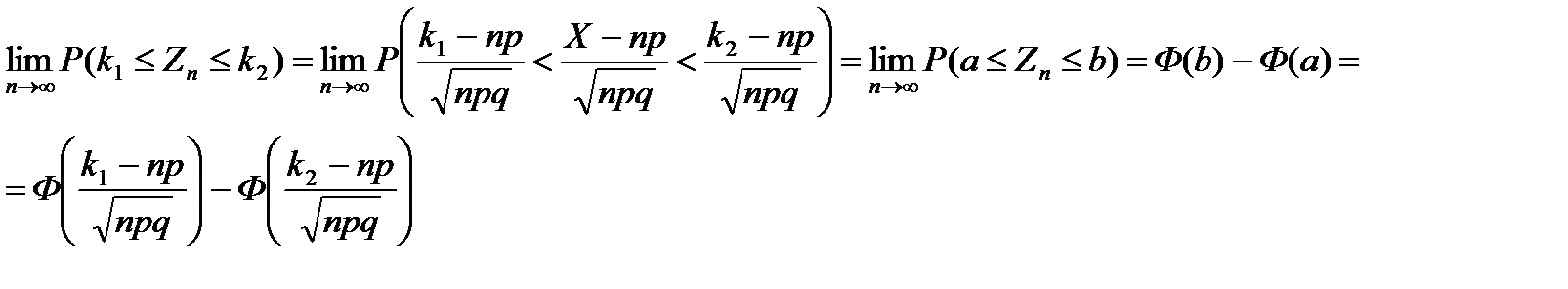
где мы использовали ранее полученные формулы

М[Х]=nр, D[Х]=nрq.

Когда n большое, но конечное, имеем приближенную формулу

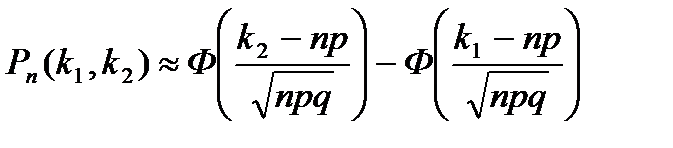
Эта формула не что иное как приближенная интегральная формула Лапласа, которую мы без доказательства использовали для подсчета аналогичной вероятности.