Приложение. Определение скорости пули баллистическим маятником (теоретический материал)
При попадании пули в мишень с пластилином, баллистический маятник приобретает угловую скорость и выходит из положения равновесия, совершая колебания вокруг своей оси. При этом считается, что скорость пули в момент соударения перпендикулярна оси и плечу маятника. Если это условие не соблюдается, то кроме вращательных, будут также возбуждаться и колебательные степени свободы маятника, т. е. ось маятника начнет совершать колебания.
Так как скорость пули перпендикулярна плоскости мишени, то момент импульса пули равен:
,
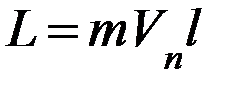где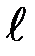 
– расстояние от оси вращения маятника до точки удара пули; m – масса пули; Vп – скорость пули.
Момент импульса системы после соударения определяется выражением:
L = IW,
где I – момент инерции системы после удара пули, равный: I = Io + 2M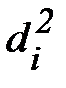 
+ ml2;
W – угловая скорость системы после удара.
Удар можно считать абсолютно неупругим, так как при соударении с мишенью пуля застревает в пластилине. В этом случае закон сохранения момента импульса примет вид:
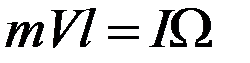(П-1)
Таким образом, после соударения баллистический маятник приобретает угловую скорость W. При движении маятника на него будет действовать момент сил, вызванный деформацией кручения стальной проволоки подвеса маятника, который равен:
,
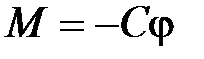где С – постоянная упругих сил кручения проволоки;
φ – угол отклонения маятника от положения равновесия.
Знак «минус» указывает, что при φ > 0, М < 0. Поэтому в момент соударения угловая скорость будет максимальной, а в дальнейшем она будет уменьшаться до нуля.
При дальнейшем движении, если не учитывать сопротивление воздуха, выполняется закон сохранения механической энергии. В момент максимального отклонения угловая скорость равна нулю, а потенциальная энергия максимальна и равна
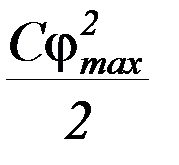
Таким образом, закон сохранения энергии мы можем записать в виде:
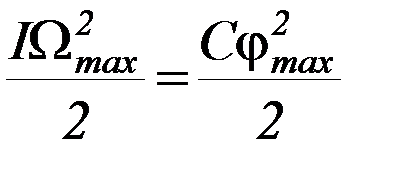, (П-2)
где φmax – максимальный угол поворота маятника.
Используя законы сохранения момента импульса (П-1) и энергии (П-2),
получаем: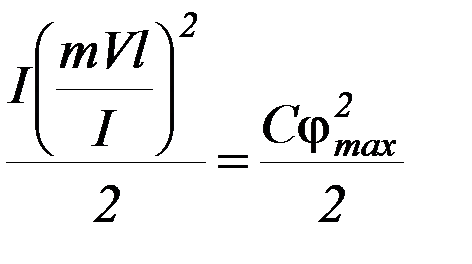 
отсюда: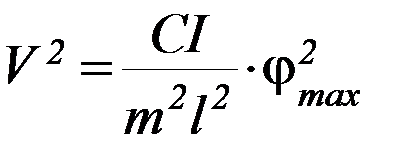 
Т. е. скорость пули до столкновения с баллистическим маятником будет определяться выражением:
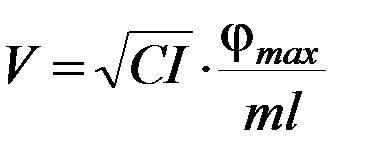(П-3)
Контрольные вопросы:
1. Дайте определение момента импульса. Как эта величина используется в лабораторной работе?
2. В чем заключается баллистический принцип?
3. Какие законы сохранения использовались в данной работе?
4. Дайте определение момента инерции.
5. Сформулируйте теорему Штейнера-Гюйгенса.
6. Как определить момент инерции баллистического маятника?
7. Как изменяется угол отклонения баллистического маятника при соударении с пулей и период его колебаний, если увеличить его момент инерции?
8. Что произойдет, если пуля попадет под углом к перпендикуляру плоскости мишени?
9. Получите формулу для определения скорости пули, если баллистический маятник после неупругого удара отклонится на максимальный угол φ.