Магнитостатическое поле

3.2.1. Объекты магнитостатики

Напомним объекты, которыми оперирует магнитостатика:

1) электрический ток I точечных зарядов. Сила тока определяется зарядом, прошедшим через поперечное сечение проводника в единицу времени . Единица силы электрического тока - ампер (А) - относится к группе основных единиц системы СИ и для этой единицы существует соответствующий материализованный эталон. Для детальной характеристики тока через поперечное сечение проводника вводят понятие плотности тока – вектор j. Модуль плотности тока численно равен отношению тока dI через элементарную площадку dS_^, расположенную перпендикулярно направлению распространения зарядов: . Плотность тока можно выразить через скорость упорядоченного движения зарядов v и плотность зарядов r =: = = = rv, т.е. j = rv;

2) магнитное поле. Основной характеристикой магнитного поля является вектор индукции магнитного поля B. Источником магнитостатического поля является электрический ток. Магнитное поле действует с определенным механическим моментом силы M на виток с током. Под действием момента пары сил (пары сил Ампера) плоскость витка поворачивается перпендикулярно силовым линиям магнитного поля. Индукция магнитного поля B определяется моментом силы M, действующим на плоский виток с единичным магнитным моментом p_m: , где p_m = IS – магнитный момент витка с током, S – площадь, охватываемая витком, I – ток в витке. Единицей магнитной индукции служит тесла (Тл): .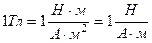

3.2.2. Поток вектора индукции магнитного поля B через

Замкнутую поверхность

Источником магнитного поля является электрический ток I или же движущиеся заряженные частицы (например, электроны, ионы). В природе не обнаружены частицы, обладающие магнитным зарядом (не обнаружены магнитные монополи). Силовые линии индукции B замкнуты сами на себя - магнитное поле имеет вихревой характер. Вследствие вихревого характера магнитного поля поток вектора B через замкнутую поверхность всегда равен нулю (силовые линий индукции B, вошедшие в рассматриваемый объем, ограниченный поверхностью S, обязательно где-то выйдут из этого объема). Итак, имеем:

= 0. (1)

Соответствующая дифференциальная форма запишется в виде:

div B = 0 или ÑB = 0. (2)

Относительно декартовой системы координат (11) имеет вид:

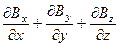= 0. (3)

3.2.3. Закон Био-Савара-Лапласа

Магнитное поле движущегося заряда. Напомним, опыты Эрстеда и другие аналогичные опыты показали, что источником магнитного поля является электрический ток, т.е. движущиеся заряды. Силовые линии индукции магнитного поля Bзамкнуты сами на себя (магнитное поле вихревое). Направление силовых линий определяется правилом правого винта: поступательное движение винта должно совпадать с направлением движения положительного заряда, тогда вращение винта будет указывать направление силовых линий вектора B.

Заряд q, движущийся со скоростью v, порождает магнитное поле. Из обобщения опытов следует, что индукция B этого поля является функцией заряда q, скорости vи радиус-вектора r, проведенного от заряда к рассматриваемой точке поля: B = f (q, v, r). С формальной точки зрения из двух разноименных векторов vи rможно получить третий вектор B только операцией векторного произведения. Таким образом, в законе для вектора B должен присутствовать член [v, r]. Далее, из опыта также следует, что индукция подчиняется закону обратного квадрата расстояния рассматриваемой точки поля от заряда:B ~ . Запишем закон индукции магнитного поля движущегося заряды

B = , (4)

где m₀ – магнитная постоянная; = 10^-7 .

ИндукцияB магнитного поля тока I может быть определена как векторная сумма магнитных полей dB, создаваемых элементарными участками электрического тока. Плотность тока j= rv(§ 3.2.1); элементарный участок содержит заряд rdV, где r – плотность заряда, dV – объем выделенного участка. Подставив эти выражения в (4), получим:

dB = (5)

Так как jdV = Idl, то (5) можно представить в виде

dB , (5^*)

Формула (5^*) определяет индукцию магнитного поля dB, создаваемого элементом проводника длиной dl на расстоянии r от элемента проводника. Формулы (5) и (5^*) выражают закон Био-Савара-Лапласа. На рис.3-16а приведена иллюстрация закона (5^*). Модуль вектора индукции dB:

.

Направление вектора индукции dB определяется правилом векторного произведения [dl, r], включающим правило правого винта.

Интегрирование (5^*) по всем элементам тока позволяет в принципе рассчитать индукцию магнитного поля. Однако интегрирование векторной функции в общем случае является довольно громоздкой операцией. В некоторых частных случаях интегрирование векторной функции можно свести к интегрированию скалярной функции. Примером является расчет магнитное поле прямого тока. В этом случае все элементарные dB в каждой точке пространства коллинеарны, поэтому интегрирование векторной функции в конечно счете сводится к интегрированию модуля ½dB½ = dB. После интегрирования получаем, что на расстоянии a от тонкого провода, по которому течет ток I, индукция определяется выражением .

Связь электрического и магнитного молей движущегося заряда. Движущийся заряд q порождает магнитное поле, индукция которого B определяется формулой (4). С этим же зарядом q связано электрическое поле. Напряженность электрического поля заряда: E = =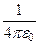

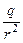
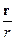Подставим = E в формулу (4), получим: B = e₀m₀ [v, E] =,где c = 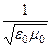равна скорости света (электромагнитного излучения) в вакууме.

3.2.4. Циркуляция индукции магнитного поля тока

Приведем без вывода теорему о циркуляции магнитного поля по контуру l, создаваемого постоянным электрическим током:

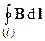=m₀ I или =I. (6)

В качестве иллюстрации теоремы (6) на рис. 3-16-б показаны четыре провода с токами I₁, I₂, I₃, I₄. Токи I₂, I₃, I₄ пронизывают поверхность, натянутую на контур. Результирующее магнитное поле B в любой точке пространства определяется векторной суммой полей от каждого из токов:

B = B₁ + B₂ +B₃ + B₄.

Однако циркуляция B по контуру l определяется алгебраической суммой электрических токов I = , которые охватываются контуром, т.е. только токи I₂, I₃ и I₄. В соответствии с направлением обхода контура и правилом правого винта, токи I₂и I₄ берутся со знаком плюс, ток I₃ – со знаком минус.

Пусть теперь произвольный контур l находится в объеме какого-нибудь проводника, по которому течет ток I. Натянем на этот контур мысленную поверхность S. Ток, пронизывающий S, можно выразить через вектор плотности тока проводимости j. Элементарный ток определяется скалярным произведением вектора плотности тока j и ориентированной площадки dS:

dI = jdS_^ = jdScosα = jdS.

Ток через конечную площадку S выразится интегралом по площади: I = 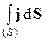. Подчеркнем, плотности тока в разных точках S могут различаться, т.е. в общем случае плотность тока является функцией координат:j = j(x, y, z).

Итак, если произвольный контур l находится в объеме проводника, то (6) можно представить в виде

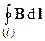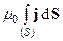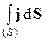= или = . (7)

В качестве примера применения теоремы о циркуляции вектора B рассчитаем поле магнитное поле соленоида (на рис. 3-17 показано сечение соленоида). Из опыта следует, что магнитное поле длинного соленоида вне его объема практически равна нулю (вне объема соленоида магнитное поле, строго говоря, не равна нулю хотя бы потому, что силовые линии магнитного поля всегда замкнуты). Направление вектора Bобразует с направлением тока правовинтовую систему. Выберем в качестве контура прямоугольник (см. рисунок).

Из теоремы о циркуляции 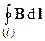=m₀ I, с учетом практического отсутствия поля вне объема соленоида, имеем: Bl = m₀nlI, где n – число витков на единице длины соленоида. Окончательно:

B = m₀nI,

где величину nI называют числом ампервитков. Магнитное поле в соленоиде однородно за исключением области торцов соленоида. Например, при I = 5 A и n = 2000 индукция магнитного поля в соленоиде B = 4p×10^-7×2000×5 = 12,56×10^-3 (Тл) = 12,56 мТл.

3.2.5. Напряженность магнитного поля H. Циркуляция H

Любое вещество является магнетиком, т.е. при помещении вещества во внешнее магнитное поле B₀ оно намагничивается. Напомним, намагничивание диа- и парамагнетиков обусловлено ориентацией магнитных моментовмолекулярных токов p_m во внешнем поле B₀, что приводит к возникновению наведенного макроскопического поля B^/. Результирующее магнитное поле будет определяться суммой внешнего и наведенного макроскопического магнитного поля B = B₀ +B^/.

Напомним вкратце механизм намагничивания вещества. Движение электрона в атоме образуют элементарный круговой ток I_м, который обычно и называют молекулярным током. Определим орбитальный магнитный момент p_m = I_мS_м молекулярного тока, где S_м – площадь, охватываемая орбитой электрона (рис. 3-18). Направление p_m определяется правилом правого винта с учетом отрицательного заряда электрона. Пусть радиус орбиты электрона r, скорость электрона v, заряд e. Имеем:

p_m = I_м S_м = = = .

Каждой электронной орбите в атоме соответствует свой молекулярный ток с соответствующим магнитным моментом, определяющим магнитное поле этого молекулярного тока. Магнитный момент каждого отдельного атома (молекулы) определяется векторной суммой орбитальных магнитных моментов всех электронов данного атома (молекулы).

Магнитный момент атома может быть равен нулю. Это возможно, если в атоме имеется четное число электроны с противоположно направленными обращениями электронов вокруг ядра атома (такие магнетики называются диамагнетиками). Если поместить диамагнетик во внешнее поле B₀, то это поле индуцирует дополнительный магнитный момент атомов. Суммарный магнитный момент атомов порождает макроскопическое магнитное поле B^/. В этом случае B^/ направлено противB₀. Уменьшение результирующего поля B относительно B₀ получило название диамагнитного эффекта. Заметим, диамагнитный эффект присущ всем без исключения магнетикам (и диа-, и пара-, и ферромагнетикам), ибо этот эффект обусловлен действием внешнего магнитного поля на электронные орбиты атомов и молекул. Чистый диамагнетик выталкивается из внешнего неоднородного поля

Атом может обладать собственным магнитным моментом, обусловленным наличием в атоме, например, нечетного числа электронов. Магнетики, атомы которых обладают собственным орбитальным магнитным моментом, называются парамагнетиками. В отсутствии внешнего поля моменты разных атомов парамагнетика направлены беспорядочно. Если поместить парамагнетик во внешнее поле B₀, то магнитные моменты атомов поворачиваются в направлении внешнего поля, порождая макроскопическое магнитное поле B^/, т.е. вещество намагничивается. Так как в парамагнетике B^/ направлено в сторону внешнего магнитного поля B₀, а диамагнитный эффект сравнительно мал, то в парамагнетиках B > B₀. Парамагнетик втягивается во внешнее неоднородное магнитное поле. Физика ферромагнетиков сложнее и обусловлена обменным взаимодействием электронов.

Степень намагничивания характеризуется вектором намагниченности J, определяемый как магнитный момент молекулярных токов единицы объема магнетика:

J = .

Алгебраическая сумма упорядоченных молекулярных токов в магнетике, находящемся во внешнем магнитном поле, образует макроскопический электрический ток в магнетике. Если магнетик однородный, то сумма молекулярных токов образует макроскопический поверхностный ток; если магнетик неоднородный, то возникает также и объемный макроскопический ток. Макроскопические токи в магнетике, формируемые внешним магнитным полем B₀, обычно называют токами намагничивания. Обозначим ток намагничивания через I^/. Можно показать, что циркуляция J по произвольному контуру l равна алгебраической сумме токов намагничивания, охватываемых контуром l:

= I^/. (8)

Единицей вектораJ служит 1 А/м.

Источником магнитного поля является электрический ток и этими токами в магнетике могут быть как токи проводимости I, так и макроскопические токи намагничивания I^/. Ток проводимости I обусловлен движением свободных зарядов в магнетике, ток намагничивания – алгебраической суммой молекулярных токов в атомах и молекулах магнетика. Циркуляция магнитной индукции Bпо произвольному контуру l в магнетике будет, разумеется, определяться и токами проводимости I, и токами намагничивания I^/, охватываемые контуром l:

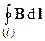=m₀ (I + I^/). (9)

Подставив (8) в (9), получим:

= I, (10)

где с правой стороны уравнения (10) стоит ток проводимости I = 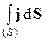, j– плотность тока проводимости.

Введем вспомогательный вектор . Вектор H называется напряженностью магнитного поля. Теперь уравнение (10) запишется в виде:

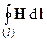= I или 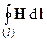= 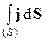, (11)

Циркуляция H по произвольному контуру l определяется только токами проводимости, которые в принципе могут быть измерены амперметром. Единица напряженности H магнитного поля совпадает с единицей намагниченности J: 1 А/м.

Намагниченность J определяется магнитным полем B в магнетике, однако принято намагниченность выражать не через индукциюB, а через напряженность Hв магнетике. Для линейных магнетиков намагниченность пропорциональна напряженности магнитного поля:

J = c_м H, (12)

где c_м – магнитная восприимчивость магнетика. Напомним: в диамагнетиках c_м < 0, в парамагнетиках c_м > 0. В ферромагнетиках c_м >> 1, однако, следует иметь в виду, что магнитная восприимчивость ферромагнетиков зависит от магнитного поля B.

Теперь можно выразить связь между B и Hв другой форме. Подставим в определение соотношение (12), получим: (1+ c_м)H = , или

B = mm₀ H, (13)

где m = (1+ c_м) – магнитная проницаемость среды.

Подчеркнем, напряженность магнитного поля H зависит как от токов проводимости, так и токов намагничивания (это следует, например, из определения , где J определяется токами намагничивания), однако циркуляция вектора H определяется только токами проводимости. Вектор H во многих случаях упрощает описание магнитного поля в магнетике. Собственно, это и оправдывает введение в структуру теории магнетизма вспомогательного вектора H.

3.2.6. Сила Лоренца, сила Ампера

Опыт показывает, что в магнитном поле с индукцией B на движущийся заряд q действует сила, определяемая законом:

F_м = q[v, B], (14)

где v – скорость заряда.

Если в пространстве содержится еще и электрическое поле с напряженностью E, то на движущийся заряд действует сила

F = F_э + F_м = qE + q[v, B]. (15)

Сила (15) называется силой Лоренца [часто силой Лоренца называют только магнитную составляющую (14)].

Сравним электрическую и магнитную составляющие силы Лоренца. Допустим, два одинаковых заряда q₁ = q₂ = q движутся параллельно друг другу относительно лаборатории с одинаковыми скоростями v₁ = v₂ = v. В этом случае модуль магнитной силы, действующей, допустим, на второй заряд со стороны магнитного поля, порождаемого первым зарядом, равен F_м = qvB, а модуль электрической силы - F_э = qE. Индукция магнитного поля движущегося заряда связана с напряженностью электрического поля этого заряда соотношением B = (см. § 3.2.3). Получаем: = . Например, при скорости зарядов v = 30000 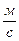получаем соотношение = 10^-8. Таким образом, при обычных скоростях зарядов (v << c) магнитная сила составляет ничтожную долю от полной силы Лоренца (15), т.к. F_м << F_э.

Если в проводнике существует электрический ток, то на каждый заряд в этом проводнике действует магнитная сила Лоренца (14). Суммарная сила, действующая на заряды, передается всему проводу. Таким образом, на проводник с током в магнитном поле действует магнитная сила, называемая силой Ампера. Выразим закон силы Ампера.

Элементарный участок содержит заряд rdV, где r – плотность заряда, dV – объем выделенного участка. Плотность тока j= rv(§ 2.1) и jdV = Idl, поэтому формулу (14) можно представить в виде:

dF = r [v, B] dV или dF = I [dl, B], (16)

где dl – длина элемента проводника. Формулы (2.16) определяют силу Ампера, действующую со стороны магнитного поля на элемент проводника с током.

В частности, из (16) следует, что модуль силы Ампера, действующей на прямой провод с током I, определится формулой F = IlB sina. Здесь l = ½l½– длина проводника, находящегося в магнитном поле (активная часть проводника), a - угол между векторами lи B. Направление вектора l совпадает с направлением тока (т.е. с направлением движения положительных зарядов). Направление силы Ампера удобно определять правилом левой руки (напомним, правило левой руки следует из правила векторного произведения).