Как вычисляется возможная работа внутренних сил?

Пусть мы имеем два состояния. Первому из них отвечают внутренние силы , а второму – . Тогда, используя формулу (15.4) и устраняя в ней коэффициент , получим следующее выражение для работы внутренних сил первого состояния на перемещениях, вызываемых силами второго состояния, и наоборот:

15.9. Как определяются прогибы и углы поворота в балке методом Мора?

Рассмотрим балку, изображенную на рис. 15.5, а.

Эту балку будем называть заданной. Обозначим и , соответственно, изгибающий момент и перерезывающую силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки в точке K.

Введем в рассмотрение вспомогательную балку, представляющую собой ту же самую балку. Нагрузим ее только одной силой (рис. 15.5, б). Эту единичную силу мы приложим в точке K, то есть в той самой точке, где мы и собираемся определить прогиб.

Внутренние усилия, возникающие во вспомогательной балке, обозначим и .

Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки, равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки.

Тогда

. (15.5)

При определении перемещений в балке, как правило, можно пренебрегать влиянием перерезывающей силы, то есть второе слагаемое в (15.5) можно отбросить. Тогда, учитывая, что , окончательно получим:

.

Эту формулу в 1874 г. получил Мор. Определение перемещений по этой формуле часто называют определением перемещений методом Мора, а саму формулу – интегралом Мора.

Необходимо иметь в виду, что входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.

Заметим, что если мы хотим в некоторой точке K определить угол поворота поперечного сечения , то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент
(рис. 15.5, в).

15.10. Как практически определяются перемещения (прогиб и угол поворота поперечного сечения) балки методом Мора?

Приведем порядок вычисления перемещений балки методом Мора:

1) к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие (при определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент );

2) для каждого участка балки составляем выражения для изгибающих моментов заданной и вспомогательной балок;

3) вычисляем интеграл Мора для всей балки по соответствующим участкам;

4) если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия (отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия).

Пусть, например, для шарнирно опертой балки постоянной изгибной жесткости , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.6, а), требуется определить прогиб посредине пролета и угол поворота на левой опоре .

Начнем с определения прогиба.

В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис. 15.6, б).

Записываем выражения для изгибающих моментов для каждого из двух участков ( ) заданной и вспомогательной балок:

.

Вычисляем интеграл Мора. Учитывая симметрию балки, получим:

.

Переходим к определению угла поворота поперечного сечения балки на левой опоре.

Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.6, в).

Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка ( ):

; .

Тогда интеграл Мора будет иметь вид:

.

Полученный нами положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .

15.11. Чему равна потенциальная энергия деформации стержня?

Согласно закону сохранения энергии, работа внешних сил не исчезает, а переходит в потенциальную энергию V, накапливаемую в упругом теле при его деформировании. Следовательно, потенциальная энергия деформации численно равна работе внешних сил при нагружении тела (или работе внутренних сил, совершаемой ими в процессе разгружения).

Обращаем внимание Читателя на присутствие в этом предложении слова «численно». Его необходимо добавлять потому, что потенциальная энергия и работа являются разными понятиями и что они не могут быть равны друг другу.

Таким образом, потенциальная энергия стержня, испытывающего, например, растяжение, кручение и прямой поперечный изгиб, равна:

.

Как видно из этой формулы, потенциальная энергия деформации всегда положительна, поскольку она является квадратичной функцией обобщенных сил (или обобщенных перемещений, так как последние линейно связаны с обобщенными силами).

Отсюда следует, что потенциальная энергия, накопленная в результате действия группы сил, не равна сумме потенциальных энергий, накопленных от действия каждой нагрузки в отдельности.

Следовательно, принцип независимости действия сил при вычислении потенциальной энергии деформации не применим.

15.12. Как формулируется теорема Кастильяно?

Пусть на упругое тело в точке K действует одна внешняя сила 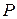. Если нагрузка получит приращение , то потенциальная энергия деформации увеличится на величину и станет равной

.

Отсюда следует, что

,

то есть производная от потенциальной энергии деформации по внешней силе дает перемещение, соответствующее этой силе.

Эта теорема в 1875 г. была доказана итальянским ученым Карло Альберто Кастильяно (Castigliano, 1847 – 1884 гг.).

Если к телу приложено несколько нагрузок, теорема Кастильяно формулируется следующим образом: перемещение точки приложения обобщенной силы по направлению ее действия равно частной производной от потенциальной энергии деформации по этой силе, то есть

.

Для определения перемещения (линейного или углового) в точке, где по условию задачи внешнее усилие (сила или момент) отсутствует, необходимо приложить в этом месте фиктивную обобщенную силу. Далее следует написать выражение для потенциальной энергии деформации от всех сил, включая и фиктивную, и взять от этого выражения производную по фиктивной силе. В полученном выражении для обобщенного перемещения фиктивную нагрузку необходимо принять равной нулю.

Продемонстрируем применение теоремы Кастильяно на следующем примере. Определим угол поворота поперечного сечения в точке K жестко защемленной балки, нагруженной распределенной нагрузкой q (рис. 15.7, а). Приложим к заданной балке на ее свободном конце в точке K фиктивный момент (рис. 15.7, б).

Изгибающий момент в произвольном сечении балки равен:

.

Потенциальная энергия деформации при изгибе балки (при пренебрежении влиянием перерезывающей силы) вычисляется по формуле

.

Угол поворота равен:

.

Принимая в полученном выражении , окончательно найдем:

.

Теорему Кастильяно можно использовать и для раскрытия статической неопределимости. Рассмотрим, например, один раз статически неопределимую балку (рис. 15.8, а).

Для определения опорных реакци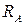й и 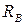, а также момента в жесткой заделке мы имеем только два уравнения статики: и . Мысленно удалим лишнюю связь – правую опору и вместо нее введем в рассмотрение неизвестную опорную реакцию 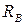, которую мы будем рассматривать как активную силу (рис. 15.8, б). Однако перемещение полученной таким образом статически определимой балки в точке приложения силы 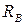должно быть равно нулю, поэтому .

Составим выражение для изгибающего момента в произвольном сечении статически определимой балки:

.

Потенциальная энергия деформации балки будет равна:

Так как перемещение в месте приложения неизвестной силы равно нулю, то

,

тогда

.

Решая последнее уравнение, находим реакцию правой опоры:

.

Теперь, составляя уравнения статики для исходной балки (см.
рис. 15.8, а), мы можем легко определить две остальные опорные реакции:

;

.

Эти результаты полностью совпадают с результатами, полученными нами другим способом для аналогичной статически неопределимой балки в беседе 7.

15.13. Как формулируется теорема Лагранжа?

Частная производная от потенциальной энергии деформации по любому обобщенному перемещению равна обобщенной силе, действующей по направлению этого перемещения, то есть

.

заключение