Задания по теме «Ряды»
Выражение вида
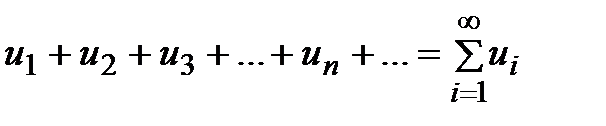 ,
,
где – 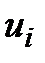 члены ряда,
члены ряда, 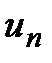 – n-й или общий член ряда, называется бесконечным рядом.
– n-й или общий член ряда, называется бесконечным рядом.
Если члены ряда:
· числа, то ряд называется числовым;
- числа одного знака, то ряд называется знакопостоянным;
- числа разных знаков, то ряд называется знакопеременным;
- положительные числа, то ряд называется знакоположительным;
· числа, знаки которых строго чередуются, то ряд называется знакочередующимся;
- функции, то ряд называется функциональным;
- степени х, то ряд называется степенным;
· тригонометрические функции, то ряд называется тригонометрическим.
Числовые ряды. Ряды с положительными членами
Основные понятия числового ряда
Числовым рядом называется сумма вида
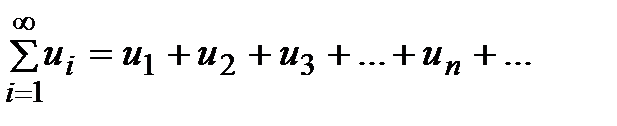 , (1)
, (1)
где 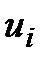 называемые членами ряда, образуют бесконечную последовательность; член
называемые членами ряда, образуют бесконечную последовательность; член 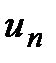 называется общим членом ряда.
называется общим членом ряда.
Суммы:
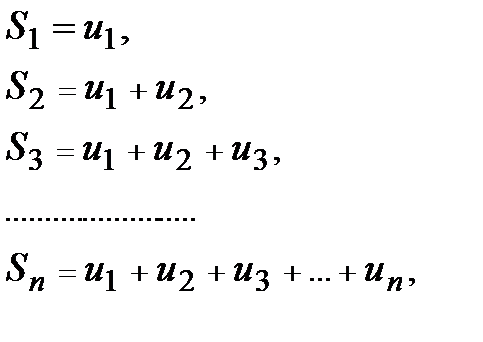
составленные из первых членов ряда (1), называются частичными суммами этого ряда.
Каждому ряду можно сопоставить последовательность частичных сумм 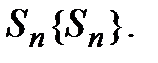
Если при бесконечном возрастании номера n частичная сумма ряда 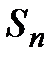 стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е.
стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е.
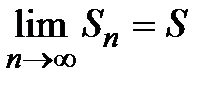 и
и 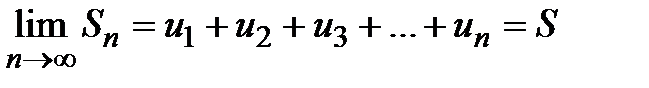 .
.
Эта запись равносильна записи
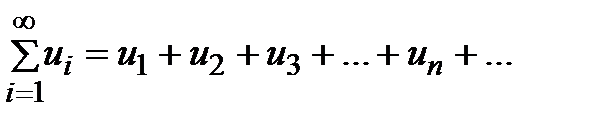 .
.
Если частичная сумма ряда (1) при неограниченном возрастании n не имеет конечного предела (стремится к 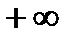 или
или 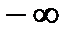 ), то такой ряд называется расходящимся.
), то такой ряд называется расходящимся.
Задание 1. Найти общий член числового ряда:
1) 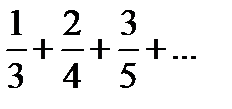 2) 2) 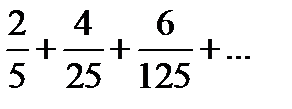 3) 3) 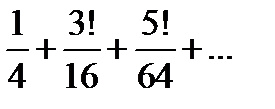 4) 4) 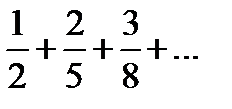 5) 5) 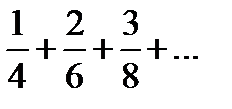 | 6) 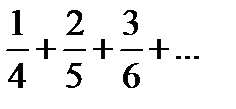 7) 7) 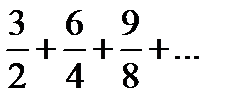 8) 8) 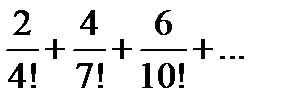 9) 9) 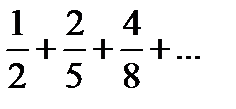 10) 10) 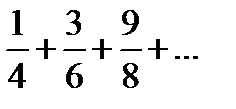 |
Необходимый признак сходимости ряда
Ряд 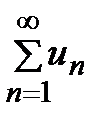 может сходиться только при условии, что его общий член при неограниченном увеличении номера n стремится к нулю:
может сходиться только при условии, что его общий член при неограниченном увеличении номера n стремится к нулю: 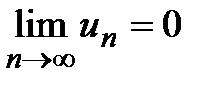 . Если
. Если 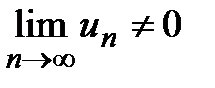 , то ряд
, то ряд 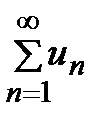 расходится – это достаточный признак расходимости ряда.
расходится – это достаточный признак расходимости ряда.
Задание 2. Проверить выполнение необходимого условия сходимости ряда:
1) 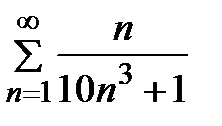 2) 2) 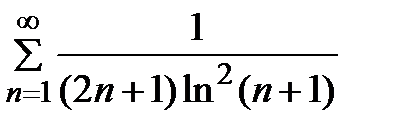 3) 3) 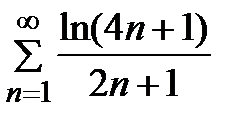 4) 4) 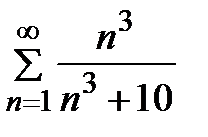 5) 5) 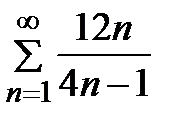 | 6) 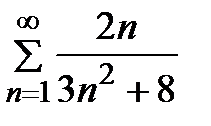 7) 7) 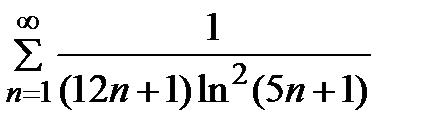 8) 8) 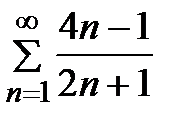 9) 9) 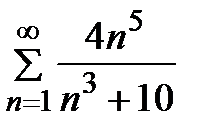  10) 10) 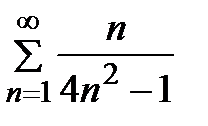 |
Достаточные признаки сходимости ряда с положительными членами.
Признаки сравнения рядов с положительными членами
1-й признак сравнения.Пусть 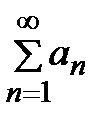 и
и 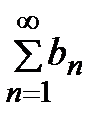 − ряды с положительными
− ряды с положительными
членами, причём 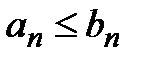 для всех номеров n, начиная с некоторого. Тогда:
для всех номеров n, начиная с некоторого. Тогда:
1) если ряд 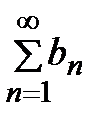 сходится, то сходится и ряд
сходится, то сходится и ряд 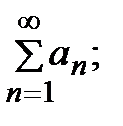
2) если ряд 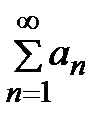 расходится, то расходится и ряд
расходится, то расходится и ряд 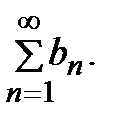
2-й признак сравнения.Пусть 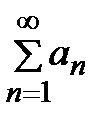 и
и 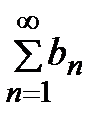 −ряды с положительными членами, причём существует конечный и отличный от нуля предел
−ряды с положительными членами, причём существует конечный и отличный от нуля предел 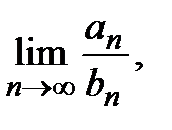 тогда ряды
тогда ряды 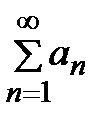 и
и 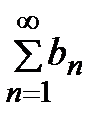 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Ряд Дирихле
Ряд 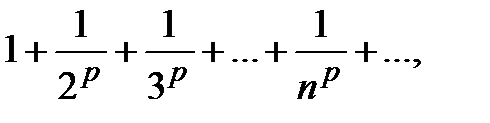 где p>0, называется рядом Дирихле. Этот ряд сходится при
где p>0, называется рядом Дирихле. Этот ряд сходится при 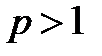 и расходится при
и расходится при 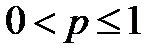 . Частным случаем ряда Дирихле (при
. Частным случаем ряда Дирихле (при 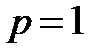 ) является гармонический ряд
) является гармонический ряд 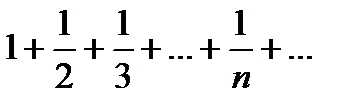 .
.
Задание 3. Исследовать на сходимость по признакам сравнения:
1) 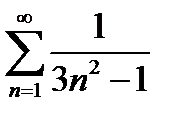 | 6) 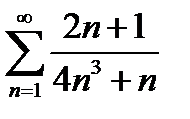 |
2) 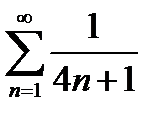 | 7) 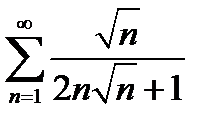 |
3) 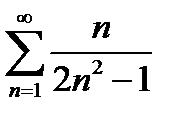 | 8) 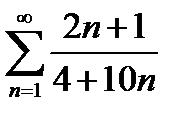 |
4) 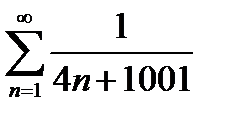 | 9) 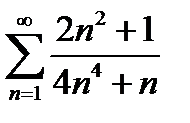 |
5) 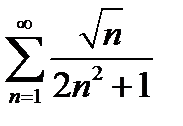 | 10) 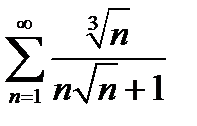 |
Признак Даламбера. Если для ряда с положительными членами 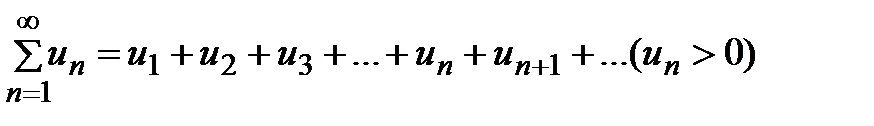 выполняется условие
выполняется условие 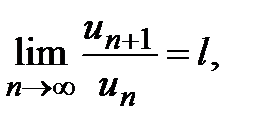 то ряд сходится при
то ряд сходится при 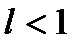 и расходится при
и расходится при 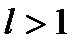 .
.
Признак Даламбера не даёт решения, если 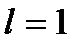 . В этом случае для исследования ряда применяются другие признаки.
. В этом случае для исследования ряда применяются другие признаки.
Задание 4. Исследовать на сходимость по признаку Даламбера:
1) 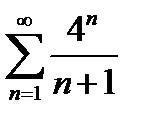 | 6) 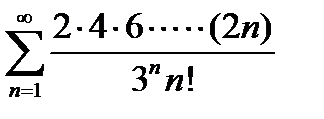 |
2) 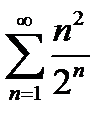 | 7) 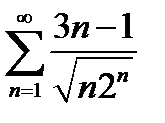 |
3) 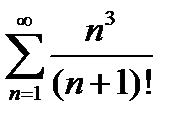 | 8) 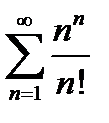 |
4) 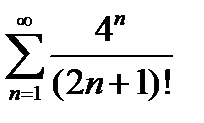 | 9) 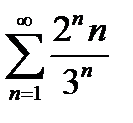 |
5) 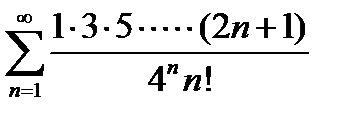 | 10) 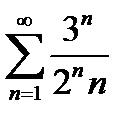 |
Интегральный признак Коши.Пусть функция f(x) при x ≥1 удовлетворяет условиям:
1) непрерывна,
2) положительна,
3) монотонно убывает.
Тогда числовой ряд 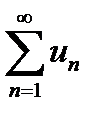 , где
, где 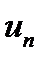 =f(n), n ≥1 сходится или расходится
=f(n), n ≥1 сходится или расходится
одновременно со сходимостью или расходимостью интеграла 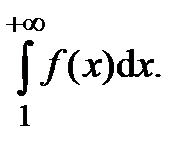
Задание 5. Исследовать на сходимость по интегральному признаку Коши следующие ряды:
1) 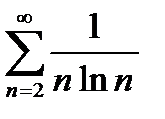 2) 2) 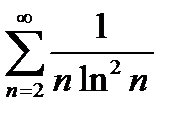 3) 3) 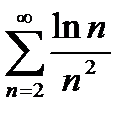 4) 4) 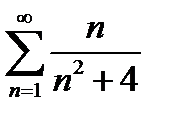 5) 5) 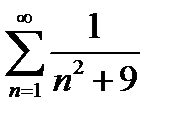 | 6) 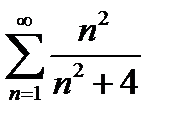 7) 7) 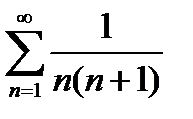 8) 8) 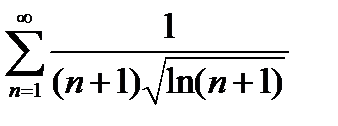 9) 9) 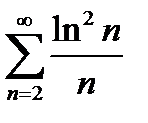 10) 10) 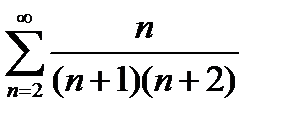 |
Знакопеременные ряды
