Синусоидальный ток в активном сопротивлении

При протекании электрического тока выделяется энергия в виде тепла или механической работы. Параметр электрической цепи, характеризующий этот процесс, называется активным сопротивлением. Количественно он определяется следующим образом. Пусть на некотором участке цепи за время Т, равное периоду переменного тока, действующее значение которого I, необратимо преобразуется в тепло или механическую работу электрическая энергия WТ. Тогда активное сопротивление рассматриваемого участка цепи по определению равно
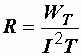. (2.12)

На схеме активное сопротивление обозначается точно так же, как и сопротивление постоянному току (рис. 2.16). Последнее, называемое еще омическим, определяется структурой кристаллической решетки проводника и состоянием свободных электронов. Наличие вблизи каких-либо проводящих тел и ферромагнитных сердечников на омическое сопротивление не влияет.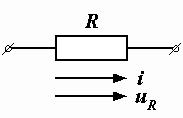

Рис. 2.16. Активное сопротивление

Иначе обстоит дело при переменном токе.
При невысоких частотах сопротивление проводника мало отличается от сопротивления постоянному току. Но с повышением частоты все сильнее и сильнее сказывается поверхностный эффект, заключающийся в вытеснении переменного тока из серединных областей проводника к его поверхности. Это приводит к уменьшению сечения, занимаемого током, к увеличению сопротивления и возрастанию тепловых потерь. К аналогичным последствиям приводит и эффект близости, выражающийся в возникновении неравномерности распределения электрического тока по сечению проводника из-за действия магнитного поля соседних проводов.
Если вблизи катушки имеются ферромагнитные сердечники и какие-либо другие проводящие тела, то магнитное поле переменного тока индуцирует в них вихревые токи, что вызывает дополнительные потери энергии на нагрев. Кроме того, в переменном магнитном поле происходит непрерывное периодическое перемагничивание ферромагнитного сердечника, требующее энергетических затрат на изменение направления магнитных моментов доменов.
Таким образом, понятие активного сопротивления является более широким, по сравнению с омическим. Числитель в формуле (2.12) при переменном токе всегда больше, чем при постоянном, так как он включает в себя все перечисленные потери электромагнитной энергии на тепло. Поэтому для одной и той же электрической установки активное сопротивление переменному току всегда оказывается больше чем сопротивление постоянному току.
Мгновенные значения напряжения и тока в активном сопротивлении связаны законом Ома:
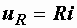или

,
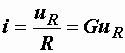где 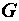– активная проводимость: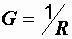

При изменении тока по синусоидальному закону

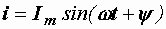(2.13)

напряжение тоже синусоидально и имеет с током одинаковые начальные фазы:

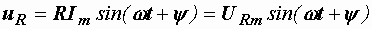. (2.14)

Отсюда

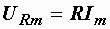или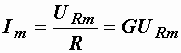

Разделив два последних уравнения на 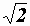, получим

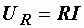и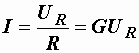

Четыре последних уравнения представляют собой различные формы записи закона Ома для активного сопротивления.
По уравнениям (2.13) и (2.14) можно записать комплексные амплитуды тока и напряжения:
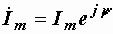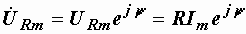, , откуда

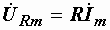или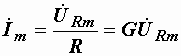

После деления последних двух уравнений на будем иметь:

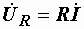и .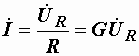

Получили те же самые выражения закона Ома, но в символической форме.
На рис. 2.17 показаны волновая и векторная диаграммы, построенные по формулам (2.13) и (2.14).

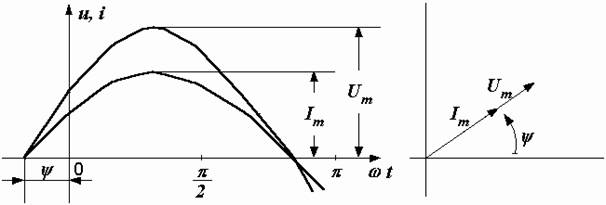
Рис. 2.17. Волновая и векторные диаграммы для активного сопротивления
В активном сопротивлении напряжение и ток совпадают по фазе; их начальные фазы одинаковы, угол сдвига фаз равен нулю, векторы на векторной диаграмме направлены в одну сторону (параллельны).