Сравнения с одним неизвестным

Будем рассматривать сравнения вида a₀xⁿ + a₁x^n-1 + … + a_n≡ 0 (mod m) (*).

Если a₀ не делится на m, то n называется степенью сравнения.

Решить сравнение – значит найти все x, ему удовлетворяющие. Два сравнения, которые удовлетворяют одни и те же значения x, называются равносильными.

Если сравнению (*) удовлетворяет какое-то x=x₁, то ему же будут удовлетворять все числа, сравнимые с x₁ по модулю m: x ≡ x₁(mod m). Весь класс чисел, сравнимых с x₁ по модулю m считается за одно решение. Таким образом, (*) будет иметь столько решений, сколько вычетов из полной системы ему удовлетворяет.

Пример:

x⁵+x+1=0 (mod 7) удовлетворяют x ≡ 2 (mod 7) и x ≡ 4 (mod 7) – 2 решения.

Сравнения первой степени.

Любое сравнение первой степени можно привести к виду ax ≡ b (mod m). Рассмотрим случай, когда (a, m)=1. Согласно утверждению 2 пункта 3 §3, когда x пробегает полную систему вычетов по модулю m, ax тоже пробегает полную систему вычетов по по модулю m. Следовательно, при одном и только одном значении x из полной системы вычетов, ax будет сравнимо с b, т.е. при (a, m)=1 сравнение имеет ровно 1 решение.

Нахождение решения: Так как (a, m) = 1, то по теореме обратимости 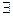a^-1 , и тогда исходному сравнению равносильно x ≡ a^-1∙b (mod m).

Пусть теперь (a,m)=d>1. Для того, чтобы сравнение имело решение, необходимо, чтобы d\b, иначе сравнение невозможно (свойство сравнений №14).

Если же a=a₁d, b=b₁d, m=m₁d , то исходному сравнению равносильно a₁x≡b₁(mod m₁), причем (a₁,m₁)=1 сравнение имеет 1 решение по mod m₁: x≡x₁(mod m₁), или d решений по модулю m:

x≡ x₁ (mod m),

x≡ x₁+m₁(mod m),

x≡x₁+2m₁(mod m),

…

x≡x₁+(d–1)m₁(mod m).

Пример 1.

Решить сравнение 6x = 5 (mod 35).

Вычислим НОД(6, 35), пользуясь алгоритмом Евклида:

35 = 6∙5+5,

6 = 1∙5 +1

5 = 5∙1+0 НОД(6, 35)=1.

Вычислим обратный элемент к 6 по модулю 35, пользуясь расширенным алгоритмом Евклида:

1 = 6–5=6–(35–6∙5)=6–35+6∙5= 6∙6–35

6^-1 = 6 (mod 35).

Домножим правую и левую части исходного сравнения на 6:

6^-1∙6x≡6^-1∙5(mod 35)

1∙x≡6∙5(mod 35)

Ответ: x ≡ 30 (mod 35)

Пример 2.

Решить сравнение 18x = 6 (mod 24).

Вычислим НОД(18, 24), пользуясь алгоритмом Евклида:

24 = 18 + 6;

18 = 2∙6+0 НОД(18, 24)=6.

Правая и левая части сравнения, а также модуль, делятся на 6. Разделим исходное сравнение на 6 и получим равносильное сравнение:

3x ≡ 1 (mod 4) *.

Вычислим НОД(3, 4), пользуясь алгоритмом Евклида:

4 = 1∙3 + 1;

3 = 3∙1 + 0 НОД(3, 4)=1.

Вычислим обратный элемент к 3 по модулю 4, пользуясь расширенным алгоритмом Евклида:

1=4–3 3^-1 = –1(mod 4).

Домножим правую и левую части сравнения (*) на –1:

3^-1∙3x=–1∙1 (mod 4) x≡ –1 (mod 4).

Или, переводя решение в систему наименьших неотрицательных вычетов, x≡ 3 (mod 4).

Ответ: получили 6 решений по модулю 24:

x≡ 3 (mod 24);

x≡ 7 (mod 24);

x≡ 11 (mod 24);

x≡ 15 (mod 24);

x≡ 19 (mod 24);

x≡ 23 (mod 24).

Система сравнений первой степени. Китайская теорема об остатках.

Рассмотрим систему сравнений

*

От системы сравнений вида a_ix ≡ b_i (mod m_i) можно перейти к данной способом, указанным в п.1.