Звеньев и кинематических пар

Л.А. ЧЕРНАЯ

КИНЕМАТИЧЕСКОЕ И КИНЕТОСТАТИЧЕСКОЕ ИССЛЕДОВАНИЕ

ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ

В системах Mathcad и AutoCAD

Учебное пособие

по теории механизмов и механике машин

Москва

Издательство МГТУ им. Н.Э.Баумана

УДК 531.8(075.8)

ББК 34.41

ТЗЗ

Кинематическое и кинетостатическое исследование плоских рычажных механизмов в системах Mathcad и AutoCAD

Учебное пособие по теории механизмов и механике машин Л.А.Черная

Введение.

Настоящее учебное пособие посвящено трем задачам механики машин, имеющим большое значение в инженерной практике: структурному, кинематическому и кинетостатическому анализу, применительно к плоским рычажным механизмам. Кинематическому анализу предшествует структурный анализ рычажного механизма, цель которого – выявить особенности строения механизма, определяющие последовательность проведения его кинематического и кинетостатического исследований.

Изложены графоаналитические и аналитические методы решения указанных задач, ориентированные на применение персональных компьютеров. Приводятся примеры использования систем Mathcad как средства численной реализации полученных алгоритмов в сочетании с графической визуализацией результатов, и AutoCAD для решения задач графоаналитическим методом.

Учебное пособие предназначено в помощь студентам, обучающимся по программе «Специалист», при выполнении двух домашних заданий (ДЗ) по дисциплине «Теория механизмов и машин». Пособие так же может быть полезно при работе над курсовым проектом по этой же дисциплине и слушателям ФПК, обучающимся по машиностроительным направлениям подготовки и специальностям.

Первое ДЗ – структурный и кинематический анализ плоского рычажного механизма, второе ДЗ – кинетостатический силовой расчет этого же механизма.

В ДЗ изучается четырех-, шести- или восьмизвенный плоский рычажный механизм (ПРМ) с одной степенью подвижности и вращательной или поступательной начальной парой. Выходным звеном механизма является ползун либо коромысло. Схема механизма и таблица исходных данных выбираются по указанному для каждого студента коду из сборника Заданий на ДЗ или задаются преподавателем.

Задачи каждого из ДЗ перечислены ниже и приведены требования к объему и форме представления их решения. Указаны также основные допущения, принятые на том или ином этапе исследования, причем каждое такое допущение распространяется и на все последующие подразделы.

Основной целью настоящего пособия является формирование у студентов целостной системы знаний, умений и навыков, необходимых в реальной практике проектирования современных машин. Алгоритмы и некоторые Mathcad-модули, разработанные в ДЗ, могут быть использованы в дальнейшем для успешного выполнения в V семестре курсового проекта по дисциплине «Теория механизмов и машин» [7,8] и при проектировании большинства механических систем, которые будут рассматриваться на старших курсах обучения в МГТУ им. Н.Э. Баумана.

Для достижения указанной цели, помимо некоторых фундаментальных положений и законов теоретической механики, на которых базируются используемые в ДЗ методы теории механизмов и машин, в пособии большое внимание уделяется алгоритмизации поставленных задач. Показано, как полученные алгоритмы реализовать в системах Mathcad и AutoCAD. Все это, по мнению автора, позволит значительно повысить уровень знаний студентов, привить им необходимые умения и навыки для решения практических задач в последующей инженерной и научной деятельности.

Изложенные в Пособии методы предполагают выбор индивидуальной траектории обучения, который определяется индивидуальными особенностями студента: уровень освоения материала на предыдущих этапах обучения (математика, теоретическая механика), базовая компьютерная подготовка, активность и т.д. Обязательный минимум на «3» - решение задач графоаналитическими методами в среде AutoCAD и успешная защита каждого домашнего задания. Использование в ДЗ аналитических методов расчета позволит, с одной стороны, проконтролировать результаты, полученные графоаналитическими методами, с другой – при успешной защите повысить итоговую оценку.

Максимальная рейтинговая оценка за каждое ДЗ –20 баллов. К защите допускаются студенты, выполнившие ДЗ в полном объёме. За нарушение сроков без уважительных причин рейтинговая оценка может быть уменьшена на 2 балла за каждую неделю просрочки. Студент получает оценку «зачёт», если за домашнюю работу и её защиту выставлен суммарный балл не ниже 12. Домашнее задание, не набравшее этой суммы баллов, не засчитывается, студенту выдаётся новое задание в конце семестра, при этом максимальные баллы снижаются: домашняя работа – 12 баллов, защита – 4 балла. В сумме – максимум 16 баллов, допустимый минимум – 12 баллов.

1. СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА

Структурный анализ позволяет выявить особенности строения механизма, определяющие последовательность проведения его кинематического и кинетостатического исследования.

Анализ выполняется на базе структурной схемы механизма, заданной в исходных данных к ДЗ.

Допущение 1: независимо от особенностей конструктивного выполнения, все шарнирные соединения считаем вращательными кинематическими парами, а все соединения, допускающие прямолинейное относительное движение звеньев – поступательными парами, поэтому все пары рычажного механизма являются одноподвижными и относятся к пятому классу.

Основные задачи подраздела:

- анализ строения механизма на уровне звеньев и кинематических

пар (классификация звеньев и кинематических пар) и определение числа степеней свободы механизма с целью выбора начальной кинематической пары.

- анализ строения механизма на уровне кинематических групп.

- расчет числа избыточных связей в каждой кинематической группе и их устранение.

Результатом структурного анализа является символическая формула строения механизма.

Цель структурного анализа: определить степень подвижности механизма и выбрать началь­ные кинематические пары; декомпозировать механизм на простейшие кинематически оп­ределимые кинематические группы, записать символическую формулу строения механизма, проанализировать механизм на наличие избыточных связей.

Решение задач структурного анализа выполняется в системе AutoCAD на листе формата А3 или А4.

1.1. Анализ строения механизма на уровне

звеньев и кинематических пар

Решение этой задачи заключается в классификации звеньев и кинематических пар, входящих в состав механизма.Результаты такого анализа оформляются в виде таблицы звеньев и кинематических пар (Табл.1 для механизма Рис. 1).

На структурной схеме рекомендуется кинематические пары переобозначить, введя 2 индекса: верхний и нижний. В нижнем индексе указать номера звеньев, образующих пару; в верхнем – вид кинематической пары: в-вращательной или п-поступательной. При анализе следует пользоваться общепринятыми названиями подвижных звеньев рычажных механизмов:

кривошип – звено, неограниченно вращающееся вокруг неподвижной оси;

коромысло – звено, поворачивающееся вокруг неподвижной оси на ограниченный угол;

ползун – звено, совершающее прямолинейное движение;

шатун – звено, совершающее сложное движение.

Каждое из названных звеньев может выступать в роли кулисы:

кулиса – подвижное звено, несущее направляющие для другого звена;

кулисный камень – звено, движущееся в направляющих кулисы.

Рис.1.

Таблица 1

Классификация звеньев и кинематических пар

	Обозначение пары	Звенья, входящие в пару	Вид пары	Классификация пары
		0 – стойка 1 – кривошип   1- кривошип 2 – кулиса   2 – кулиса 3 – кулисный камень   3 – кулисный камень 0 - стойка	Вращательная     Вращательная     Поступательная   Вращательная	Одноподвижная, 5-го класса   Одноподвижная, 5-го класса   Одноподвижная, 5-го класса     Одноподвижная, 5-го класса

Степень подвижности механизма есть число его степеней свободы в системе координат, связанной со стойкой.

Учитывая Допущение 1, число степеней свободы плоского рычажного механизма можно вычислить по формуле П.Л.Чебышева:

, (1.1)

где 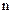- число подвижных звеньев, 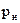- число одноподвижных кинематических пар (пятого класса), вращательных или поступательных.

Степени свободы - это совокупность линейно независимых координат, полностью определяющих положение (а вместе с их производными по времени и движение) механической системы в выбранной системе координат. Такие координаты в общем случае называются обобщёнными координатами

. (1.2)

Следовательно: степень подвижности механизма равна числу законов движения, которые необходимо задать звеньям механизма извне для того, чтобы все его звенья двигались вполне определенным образом.

При обобщенная координата приписывается начальной кинематической паре.

Начальная кинематическая пара (НКП) – кинематическая пара, в которой относительное перемещение образующих ее звеньев есть обобщенная координата. Если одно из звеньев НКП – стойка, то второе, подвижное, звено называют начальным (или входным). Начальное звено относительно стойки может совершать поступательное движение (ползун) или вращательное движение (коромысло или кривошип).

Определение степени подвижности механизма в ДЗ имеет смысл проверочного расчета, т. к. в исходных данных к типовому ДЗ начальное (входное) звено указано: это звено образует со стойкой вращательную кинематическую пару. Примем угол его поворота за обобщенную координату механизма

. (1.3)

Угловую обобщенную коор­динату 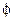будем отсчитывать от положительного на­правления оси X правой декартовой системы координат, двигаясь против хода часовой стрелки.