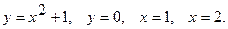Правила выполнения и оформления
КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ требуется строгое соблюдение указанных ниже правил. Работы, выполненные без соблюдения этих правил, могут быть не зачтены.
1. Контрольная работа выполняется в тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля для замечаний рецензента.
2. На обложке контрольной работы должны быть ясно написаны фамилия и инициалы студента, шифр, название дисциплины, номер и вариант контрольной работы, адрес студента. В конце работы ставится дата ее выполнения и подпись.
3. В работу включаются все задачи, указанные в задании, строго по положенному варианту.
4. Решения задач располагаются в порядке возрастания их номеров, указанных в задании, сохраняя номера задач.
5. Условия задач приводятся полностью. Решения излагаются подробно и аккуратно, объясняются все действия по ходу решения и делаются необходимые чертежи.
6. После получения проверенной работы исправляются отмеченные рецензентом ошибки и выполняются все рекомендации рецензента.
ПРОГРАММА КУРСА “МАТЕМАТИКА”
ДЛЯ СТУДЕНТОВ –- ЗАОЧНИКОВ
ИНЖЕНЕРНО – ТЕХНИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ
(ВТОРОЙ СЕМЕСТР)
Исследование функций с помощью производных
1. Условия возрастания и убывания функции. Точки экстремума Необходимое и достаточные признаки существования экстремума. Отыскание наибольшего и наименьшего значений функции, непрерывной на отрезке [1, гл. 5, §§1-6].
2. Исследование функций на выпуклость и вогнутость. Точки перегиба. Асимптоты кривых. Общая схема построения графиков функций [1, гл. 5, §§9-11].
Неопределенный интеграл
3. Первообразная. Неопределенный интеграл, его свойства. Таблица основных формул интегрирования. Непосредственное интегрирование. Интегрирование по частям и подстановкой [1, гл.10, §§1-4,6].
4. Интегрирование рациональных функций путем разложения на простейшие дроби. Интегрирование некоторых классов тригонометрических функций. Интегрирование некоторых иррациональных выражений [1, гл. 10, §§5,7-10,12].
Определенный интеграл
5. Определенный интеграл как предел интегральных сумм. Основные свойства определенного интеграла [1, гл.11, §§1-3].
6. Производная интеграла по верхнему пределу. Формула Ньютона-Лейбница [1, гл.11, §4].
7. Вычисление определенного интеграла интегрированием по частям и подстановкой. Приближенное вычисление определенного интеграла по формулам прямоугольников, трапеций и Симпсона [1, гл.11, §§5-6,8].
8. Приложение интегралов к вычислению площадей, длин дуг кривых,объемов тел и площадей поверхностей вращения. [1, гл.12, §§1,3,5,6].
Несобственный интеграл
9. Несобственные интегралы с бесконечными пределами. Несобственные интегралы от неограниченных функций. Основные свойства. Абсолютная и условная сходимость. Признаки сходимости [1, гл. 11, § 7].
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
К КОНТРОЛЬНОЙ РАБОТЕ № 2
1. Каковы признаки возрастания и убывания функции?
Что называется экстремумом функции? Как найти максимумы и минимумы функции? Сформулируйте два правила.
2. Приведите пример, показывающий, что обращение производной в нуль не является достаточным условием экстремума функции.
3. Чем отличается максимум (минимум) функции, заданной на некотором отрезке, от ее наибольшего (наименьшего) значения?
4. Как найти наибольшее и наименьшее значения функции на отрезке? Всегда ли они существуют?
5. Как находятся интервалы выпуклости и вогнутости и точки перегиба графика функции? Приведите примеры.
6. Что называется асимптотой кривой?
7. Как находятся вертикальные и наклонные асимптоты графика функции?
8. Каковы основные пункты общей схемы исследования функции и построения ее графика?
9. Дайте определение первообразной функции и неопределенного интеграла.
10. Напишите таблицу основных интегралов.
11. Сформулируйте основные свойства неопределенного интеграла.
12. Выведите формулу замены переменной в неопределенном интеграле.
13. Выведите формулу интегрирования по частям.
14. Запишите простейшие рациональные дроби I-IV типов. Вычислите неопределенные интегралы от простейших рациональных дробей I-III типов.
15. Изложите правило разложения правильной рациональной дроби на простейшие методом неопределенных коэффициентов.
16. Интегрирование иррациональных выражений.
17. Интегрирование тригонометрических выражений. Универсальная тригонометрическая подстановка.
18. Определенный интеграл и его свойства. Геометрический смысл определенного интеграла.
19. Формула Ньютона-Лейбница для вычисления определенного интеграла.
20. Интегрирование заменой переменной и по частям в определенном интеграле
21. Несобственные интегралы первого и второго рода.
22. Теоремы оценки сходимости несобственных интегралов первого и второго рода.
23. Формула площади криволинейной трапеции в декартовой системе координат.
24. Формулa площади криволинейной трапеции в полярнойсистемекоординат.
25. Формула длины дуги кривой в декартовой системе координат.
26. Формула длины дуги кривой, заданной параметрическими уравнениями.
27. Формула объема тела вращения.
КОНТРОЛЬНАЯ РАБОТА № 2
Задача № 1
Найти интервалы монотонности и точки экстремума функции 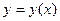 .
.
1. 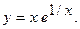 2.
2. 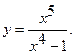
3. 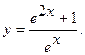 4.
4. 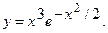
5. 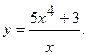 6.
6. 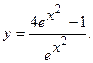
7. 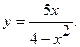 8.
8. 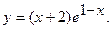
9. 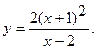 10.
10. 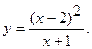
11. 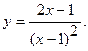 12.
12. 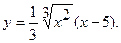
13. 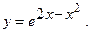 14.
14. 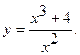
15. 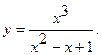 16.
16. 
17. 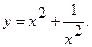 18.
18. 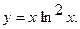
19. 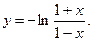 20.
20. 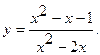
Задача № 2
Составить уравнение касательной и уравнение нормали к данной кривой в точке с абсциссой 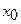
1. 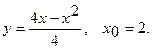 2.
2. 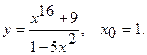
3. 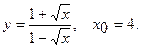 4.
4. 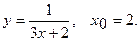
5. 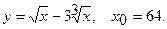 6.
6. 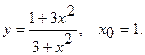
7. 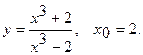 8.
8. 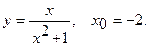
9. 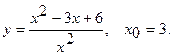 10.
10. 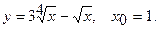
11. 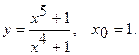 12.
12. 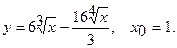
13. 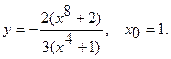 14.
14. 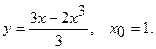
15. 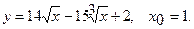 16.
16. 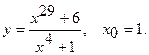
17. 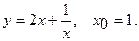 18.
18. 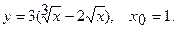
19. 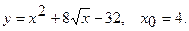 20.
20. 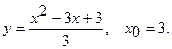
Задача № 3
Найти наибольшее и наименьшее значения функции 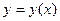 на указанном отрезке.
на указанном отрезке.
1. 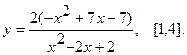 2.
2. 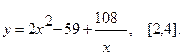
3. 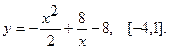 4.
4. 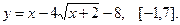
5. 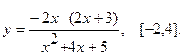 6.
6. 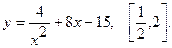
7. 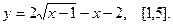 8.
8. 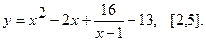
9. 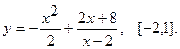 10.
10. 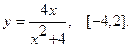
11. 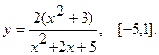 12.
12. 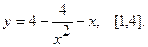
13. 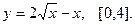 14.
14. 
15. 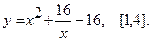 16.
16. 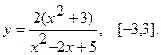
17. 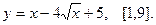 18.
18. 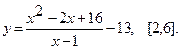
19. 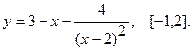 20.
20. 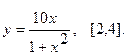
Задача № 4
Исследовать функцию 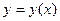 методами дифференциального исчисления и построить ее график.
методами дифференциального исчисления и построить ее график.
1. а)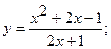 2. а)
2. а) 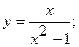
б) 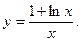 б)
б) 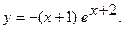
3. а)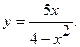 4. а)
4. а) 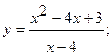
б) 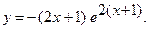 б)
б) 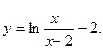
5. а)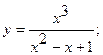 6. а)
6. а) 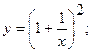
б) 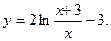 б)
б) 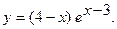
7. а) 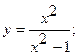 8. а)
8. а) 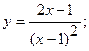
б) 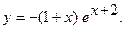 б)
б) 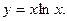
9.а) 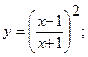 10. а)
10. а) 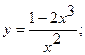
б)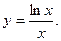 б)
б) 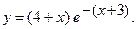
11. а) 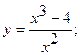 12. а)
12. а) 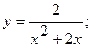
б) 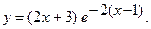 б)
б) 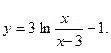
13. а) 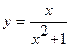 14. а)
14. а) 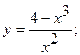
б) 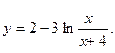 б)
б) 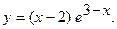
15. а) 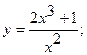 16. а)
16. а) 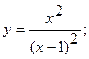
б) 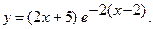 б)
б) 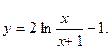
17. а) 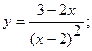 18. а)
18. а) 
б) 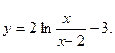 б)
б) 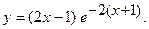
19. а) 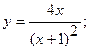 20. а)
20. а) 
б) 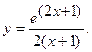 б)
б) 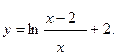
Задача № 5
Найти неопределенный интеграл.
1.а) 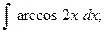 2. а)
2. а) 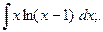
б) 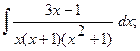 б)
б) 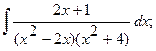
в) 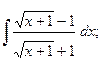 в)
в) 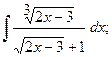
г) 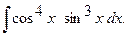 г)
г) 
3.а) 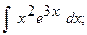 4. а)
4. а) 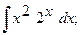
б) 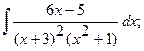 б)
б) 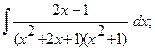
в) 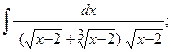 в)
в) 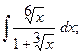
г) 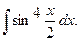 г)
г) 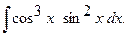
5.а) 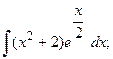 6. а)
6. а) 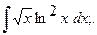
б) 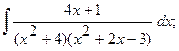 б)
б) 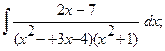
в) 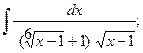 в)
в) 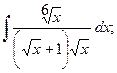
г) 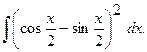 г)
г) 
7.а) 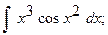 8. а)
8. а) 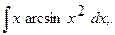
б) 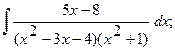 б)
б) 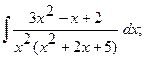
в) 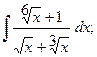 в)
в) 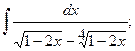
г) 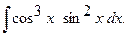 г)
г) 
9.а) 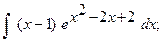 10. а)
10. а) 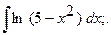
б) 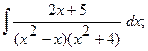 б)
б) 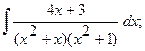
в) 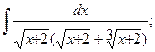 в)
в) 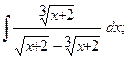
г) 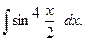 г)
г) 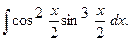
11.а) 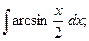 12. а)
12. а) 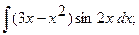
б) 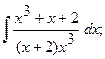 б)
б) 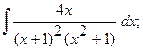
в) 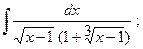 в)
в) 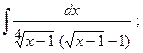
г) г)
г) 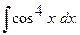
13.а) 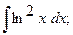 14. а)
14. а) 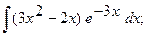
б) 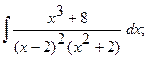 б)
б) 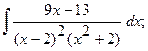
в) 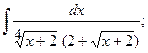 в)
в) 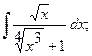
г) 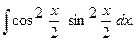 г)
г) 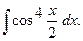
15.а) 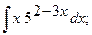 16. а)
16. а) 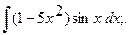
б) 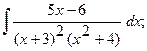 б)
б) 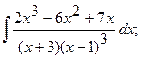
в) 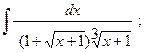 в)
в) 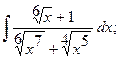
г) 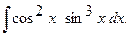 г)
г)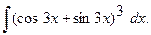
17.а)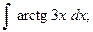 18.а)
18.а) 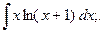
б) 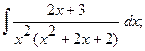 б)
б) 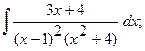
в) 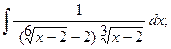 в)
в) 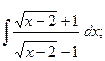
г) 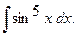 г)
г)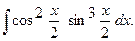
19.а)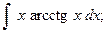 20.а)
20.а)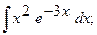
б)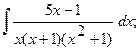 б)
б) 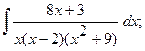
в) 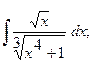 в)
в) 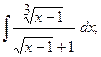
г)  г)
г) 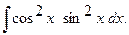
Задача № 6
Вычислить несобственный интеграл или установить его расходимость.
1. 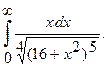 2.
2. 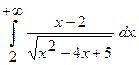
3. 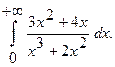 4.
4. 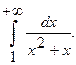
5. 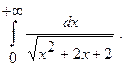 6.
6. 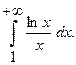
7. 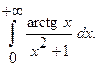 8.
8. 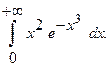
9.  10.
10. 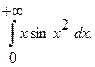
11. 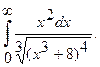 12.
12. 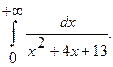
13. 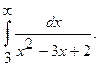 14.
14. 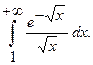
15. 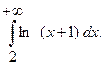 16.
16. 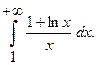
17. 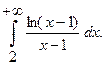 18.
18. 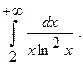
19. 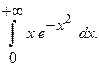 20.
20. 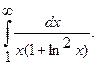
Задача № 7
Вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
1. 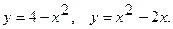
2. 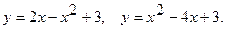
3. 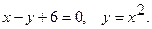
4. 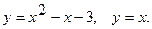
5. 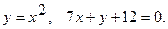
6. 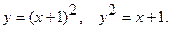
7. 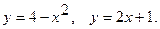
8. 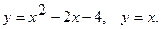
9. 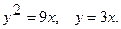
10. 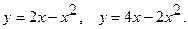
11. 
12. 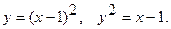
13. 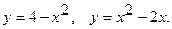
14. 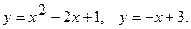
15. 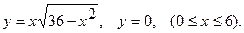
16. 
17. 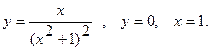
18. 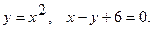
19. 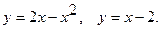
20. 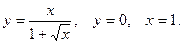
Задача № 8
Вычислить длину дуги кривой, заданной уравнениями.
1. а) 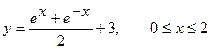 . б) . б) 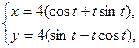 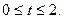 2. а) 2. а) 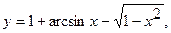 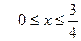 . б) . б) 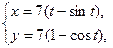 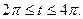 | ||
3. а) 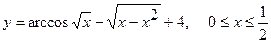 . б) . б) 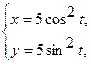 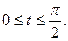 4.а) 4.а) 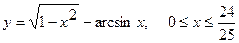 . б) . б) 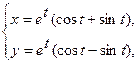 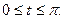 5. а) 5. а) 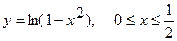 . б) . б) 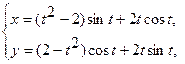 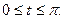 6.а) 6.а) 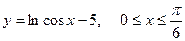 . б) . б) 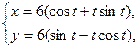 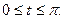 7.а) 7.а) 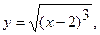 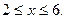 б) б)  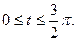 8.а) 8.а) 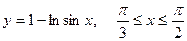 . б) . б) 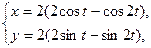 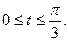 9.а) 9.а) 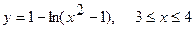 . б) . б) 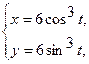 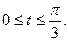 10.а) 10.а) 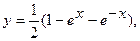 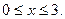 б) б) 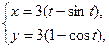 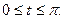 11.а) 11.а)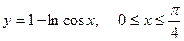 . б) . б) 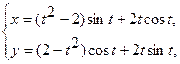  12.а) 12.а)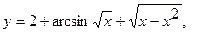 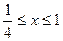 . б) . б) 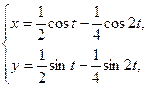 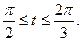 13.а) 13.а) 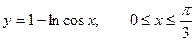 . б) . б) 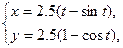 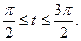 14.а) 14.а) 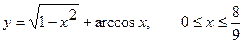 . б) . б) 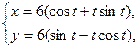 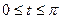 15.а) 15.а) 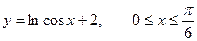 . б) . б) 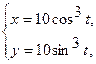 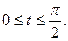 16.а) 16.а) 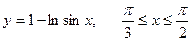 . б) . б)  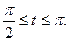 17.а) 17.а) . б) . б) 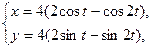 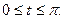 18.а) 18.а) 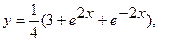 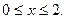 б) б) 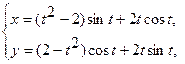 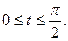 19.а) 19.а)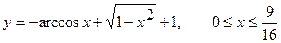 . б) . б) 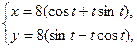 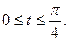 20.а) 20.а)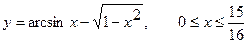 . б) . б) 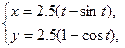 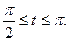 |
Задача № 9
Вычислить объем тела, полученного при вращении вокруг оси 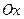 фигуры, ограниченной заданными линиями. Сделать чертеж.
фигуры, ограниченной заданными линиями. Сделать чертеж.
1. 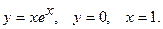
2. 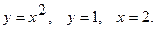
3. 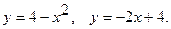
4. 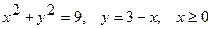 .
.
5. 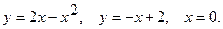
6. 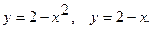
7. 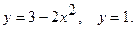
8. 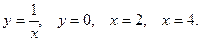
9. 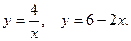
10. 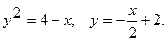
11. 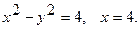
12. 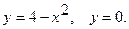
13. 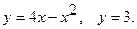
14. 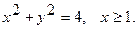
15. 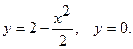
16. 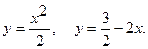
17. 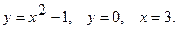
18. 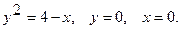
19. 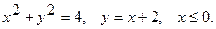
20.