Ема 2.Технология моделирования.
ема 1.Основные понятия моделирования систем.
1. Дайте определение понятий система и модель. Что означает гомоморфизм моделей?
2. Сформулируйте основные принципы физического моделирования. Приведите примеры физических моделей.
3. Дайте определение математической модели. Какая модель называется адекватной?
4. Сформулируйте основной принцип аналогового моделирования. Приведите примеры “аналогичных”, в смысле этого принципа, процессов.
5. Определите понятие алгоритмическая модель. Приведите примеры алгоритмических моделей.
6. В общей теории систем утверждается, что для систем характерно наличие интегративных свойств. Приведите пример подтверждающий это утверждение.
7. Какие свойства системы определяются морфологической моделью? Приведите пример.
8. Какие свойства модели определяются функциональным описанием? Дайте определение понятиям: состояние, статическая модель, динамическая модель. Приведите пример.
9. В чем состоит методологическая специфика системного подхода?
10. Определите понятия, на которых строится формальное описание процесса функционирования систем.
11. Приведите примеры систем функционирующих в непрерывном времени и систем функционирующих в дискретном времени.
12. Приведите примеры систем с непрерывным множеством состояний и с дискретным множеством состояний.
13. Какие общие черты и отличия имеют функциональные описания детерминированных и стохастических систем?
14. В чем состоит принципиальное различие внешних и внутренних моделей систем?
ема 2.Технология моделирования.
1. Дайте определение процесса моделирования.
2. Опишите содержательную часть описания и средства, используемые для описания системы на уровне вербальной, концептуальной и формальной моделей.
3. Какую роль играет цель разработки модели в процессе моделирования?
4. Какие функции могут выполнять математические модели?
5. Для выполнения каких функций могут быть использованы: аксиоматические модели, эмпирико-статистические модели, имитационные модели?
6. Приведите примеры аксиоматических, эмпирико-статистических и имитационных моделей.
7. Какие качества математической модели оцениваются с помощью верификации, и какие - путем проверки адекватности модели?
8. Что понимается под термином валидация модели и в каких случаях валидация применяется?
9. С какой целью выполняется анализ чувствительности модели к вариациям параметров модели и внешних воздействий?
10. Какие модели называются “грубыми”?
Тема 3 Качественный анализ. Линейные системы
- Сформулируйте основную задачу качественного анализа непрерывных систем при фиксированных значениях параметров.
- Сформулируйте основную задачу качественного анализа непрерывных систем при изменениях значений параметров.
- Что называют траекторией системы дифференциальных уравнений в фазовом пространстве?
- Что называют фазовым портретом системы дифференциальных уравнений?
- Дайте определение понятия фазовое пространство системы дифференциальных уравнений.
- Перечислите возможные типы траекторий системы дифференциальных уравнений в фазовом пространстве. Какие формы движения системы соответствуют каждому из них?
- Какие стационарные точки называют асимптотически устойчивыми?
- Какие стационарные точки называют нейтрально устойчивыми?
- Какие стационарные точки называют неустойчивыми?
- Как ведут себя фазовые траектории в окрестности асимптотически устойчивой стационарной точки?
- Как ведут себя фазовые траектории в окрестности нейтрально устойчивой стационарной точки?
- Как ведут себя фазовые траектории в окрестности неустойчивой стационарной точки?
- Дайте определение автономной системы дифференциальных уравнений.
- Дайте определение неавтономной системы дифференциальных уравнений.
- Приведите другие термины, которые можно использовать взамен понятий автономная и неавтономная системы дифференциальных уравнений.
- Сколько стационарных точек имеет линейная автономная система? Как определить эти точки?
- Напишите общее решение системы линейных дифференциальных уравнений в случае, если матрица коэффициентов не имеет нулевых и кратных собственных значений.
- Какие фазовые портреты может иметь система, приводимая к канонической форме
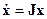 , где
, где 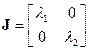 ?
? - Какие фазовые портреты может иметь система, приводимая к канонической форме
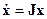 , где
, где 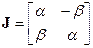 ?
? - Напишите общее решение системы линейных дифференциальных уравнений в случае, если матрица коэффициентов не имеет нулевых и кратных собственных значений.
- Какое графическое представление имеет составляющая общего решения вида
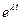 при различных вещественных значениях l?
при различных вещественных значениях l? - Какое графическое представление имеет составляющая общего решения вида
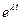 при комплексных значениях l?
при комплексных значениях l? - Какое графическое представление имеет составляющая общего решения вида
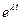 при чисто мнимых l?
при чисто мнимых l? - Как соотносятся между собой фазовые портреты канонической и неканонической систем, матрицы коэффициентов которых имеют одинаковые собственные числа?
- Приведите пример канонической системы дифференциальных уравнений имеющей фазовый портрет называемый устойчивым узлом.
- Приведите пример канонической системы дифференциальных уравнений имеющей фазовый портрет называемый неустойчивым узлом.
- Приведите пример канонической системы дифференциальных уравнений имеющей фазовый портрет называемый седлом.
- Приведите пример канонической системы дифференциальных уравнений имеющей фазовый портрет называемый неустойчивым фокусом.
- Приведите пример канонической системы дифференциальных уравнений имеющей фазовый портрет называемый устойчивым фокусом.
- Приведите пример канонической системы дифференциальных уравнений имеющей фазовый портрет называемый центром.
Тема 4 Качественный анализ. Нелинейные системы
- Дайте определение глобального и локального фазового портрета.
- В каких случаях метод линеаризации может быть использован для исследования фазового портрета в окрестностях стационарной точки нелинейной системы?
- Почему метод линеаризации не применим для качественного анализа негрубых и непростых стационарных точек нелинейных систем?
- Какая фазовая траектория называется предельным циклом?
- Какие предельные циклы являются устойчивыми, неустойчивыми, полуустойчивыми.
- Какая фазовая траектория называется сепаратриссой?
- Какие стационарные точки называются грубыми и негрубыми, почему?
Тема 5. Марковские СМО
1. Дайте определение случайного процесса.
2. Какой случайный процесс называется марковским?
3. Приведите примеры марковских случайных процессов.
4. Дайте определение графа состояний.
5. Приведите пример описания случайного процесса с помощью графа состояний.
6. Дайте определение потока событий.
7. Опишите признаки, по которым классифицируются потоки событий.
8. Какой поток называется однородным?
9. Какой поток называется неоднородным?
10. Какой поток называется регулярным?
11. Какой поток называется рекуррентным?
12. Какой поток называется потоком без последействия?
13. Какой поток называется стационарным?
14. Какой поток называется ординарным?
15. Какими основными свойствами характеризуется пуассоновский поток событий?
16. Запишите закон распределения событий на малом интервале времени в пуассоновском потоке.
17. Какому закону подчиняется распределение интервалов между событиями в пуассоновском потоке?
18. Напишите уравнения Колмогорова для пуассоновского потока событий.
19. Какое распределение описывает количество событий в пуассоновском потоке на заданном интервале времени?
20. Какие системы массового обслуживания называются марковскими?
21. Докажите, что при показательном законе обслуживания поток обслуженных заявок является потоком без последействия.
22. Приведите примеры систем обслуживания, в которых время обслуживания имеет экспоненциальный закон распределения.
23. Приведите примеры систем обслуживания, которые можно моделировать как марковские СМО.
24. Постройте граф переходов и запишите систему уравнений состояния одноканальной СМО с ожиданием.
25. Запишите уравнение расхода для одноканальной СМО с ожиданием.
26. Запишите условие существования установившегося режима в одноканальной СМО с ожиданием.
27. Определите конечные вероятности состояний одноканальной СМО с ожиданием.
28. Постройте граф переходов и запишите систему уравнений состояния многоканальной СМО с ожиданием.
29. Определите конечные вероятности состояний многоканальной СМО с ожиданием.
30. Запишите условие существования установившегося режима в многоканальной СМО с ожиданием.
31. Постройте граф переходов и запишите систему уравнений состояния многоканальной СМО с отказами.
32. Определите конечные вероятности состояний многоканальной СМО с отказами.
33. Постройте граф переходов и запишите систему уравнений состояния многоканальной замкнутой СМО.
34. Определите конечные вероятности состояний многоканальной замкнутой СМО.
35. Запишите уравнение расхода для замкнутой СМО.
36. Когда в замкнутой СМО возникает явление «скученности».
Тема 6. Имитационное моделирование
1. Дайте определение понятия имитационное моделирование.
2. Приведите примеры: дискретной имитационной модели, непрерывной имитационной модели, комбинированной дискретно-непрерывной имитационной модели.
3. Опишите взаимосвязь между понятиями событие, действие и процесс.
4. В чем состоит пороцессно-ориетированный подход к описанию имитационных моделей?
5. В чем состоят особенности функционирования комбинированных дискретно-непрерывных моделей?
6. Опишите пошаговый алгоритм продвижения модельного времени.
7. Опишите пособытийный алгоритм продвижения модельного времени.
8. Дате рекомендации к применению пособытийного и пошагового алгоритмов продвижения модельного времени.
