Прочность бруса при сложном сопротивлении
Дан плоскопространственный консольный брус из двух стержней с ломаным очертанием осевой линии. Сечение одного стержня круглое с диаметром d, сечение другого стержня прямоугольное с заданным соотношением сторон h/b. Стержни перпендикулярны между собой, Силы направлены перпендикулярно стержням или вдоль их осей, пары сил (моменты) лежат в плоскостях, перпендикулярных одному из стержней.
Требуется:
1. Построить эпюры N, Mx , My, Mк в аксонометрии.
2. Указать вид сопротивления для каждого участка бруса.
3. Определить максимальные напряжения в опасном сечении каждого участка от внутренних усилий N, Mx , My и Mk (касательными напряжениями от поперечных сил в сечениях пренебречь).
4. Из расчёта на прочность по первому предельному состоянию определить размеры поперечного сечения d, b, h.
Указание. Ориентацию прямоугольного сечения относительно координатных осей выбирает студент.
Исходные данные
| Шифр | 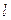 м м | a м | h/b | 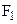 кН кН | 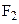 кН кН | 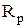 МПа МПа | 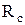 МПа МПа | 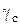 |
| 31-6 | 1,1 | 0,6 | 1,75 | 0,95 |
Расчётная схемаРешение
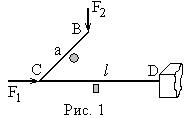 Заданы расчётные значения сопротивления материала и нагрузок. Для проверки прочности балки потребуются максимальные значения поперечной силы и изгибающего момента в сечениях. Поэтому необходимо построить соответствующие эпюры.
Заданы расчётные значения сопротивления материала и нагрузок. Для проверки прочности балки потребуются максимальные значения поперечной силы и изгибающего момента в сечениях. Поэтому необходимо построить соответствующие эпюры.
 Искомые размеры поперечных сечений зависят от внутренних сил. Поэтому займёмся их определением с помощью метода сечений. Чтобы не вычислять специально опорные реакции, в методе сечений будем рассматривать отсечённые части, не включающие заделку. Рассмотрим каждый участок отдельно.
Искомые размеры поперечных сечений зависят от внутренних сил. Поэтому займёмся их определением с помощью метода сечений. Чтобы не вычислять специально опорные реакции, в методе сечений будем рассматривать отсечённые части, не включающие заделку. Рассмотрим каждый участок отдельно.
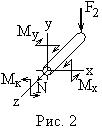
Участок BC. Отсечённая часть представлена на рис. 2. Показаны координатные оси и внутренние силы. Направления последних избираются произвольно, их действительные направления далее даются решениями уравнений. Составим уравнения равновесия и найдём из них внутренние силы
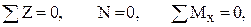
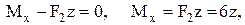
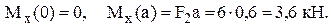

Во всех ответах получены положительные знаки, и это означает, что фактические направления внутренних сил совпадают с заранее показанными на рисунке 1.
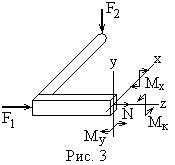 Участок CD. Отсечённая часть представлена на рис. 3. Как и в предыдущем случае составим уравнения равновесия, и найдём внутренние силы
Участок CD. Отсечённая часть представлена на рис. 3. Как и в предыдущем случае составим уравнения равновесия, и найдём внутренние силы
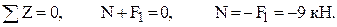
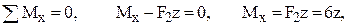
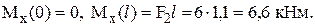
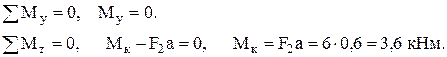
Для продольной силы получен знак минус, и это означает, что направление стрелки противоположно изображённому на рисунке 3, т.е. участок CDработает на сжатие.
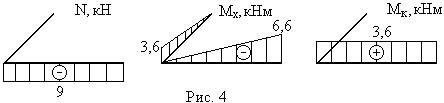 |
По результатам вычислений построены эпюры N, Mx и Mк, показанные на рисунке 4. Изгибающие моменты My тождественно равны нулю.
Перейдём к определению размеров поперечных сечений стержня. Расчётные сопротивления материала на растяжение и сжатие равны между собой. Значит, наиболее подходящей теорией прочности является энергетическая теория прочности.
Участок BС подвергается прямому поперечному изгибу. При пренебрежении поперечной силой (значит, и касательными напряжениями) здесь расчёт должен проводиться в опасном сечении по нормальному напряжению, так как напряжённое состояние получается линейным (одноосным). Опасным сечением является сечение С с максимальным изгибающим моментом Мх = 3,6 кНм. Независимо от применяемой теории прочности условие прочности по первому предельному состоянию имеет вид
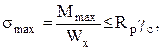 (1)
(1)
где Wх – осевой момент сопротивления поперечного сечения. Вычислим его по известной формуле для круга
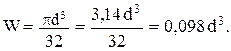
Теперь условие прочности (1) после подстановок принимает вид
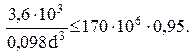
Решая, получим d = 6,1 см.
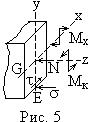 Участок СD находится в условиях сложного сопротивления, так как в его сечениях действуют сжимающая продольная сила, изгибающий момент, крутящий момент и поперечная сила (рис. 5), влиянием которой пренебрегаем, и поэтому не показываем. Опасным является сечение D, в котором сочетаются наибольшие значения N, Mx, Mк. Анализ рисунка показывает, что опасной точкой является Е, где суммируются сжимающие нормальные напряжения от продольной силы и изгибающего момента, и одновременно действует касательное напряжение от крутящего момента. Здесь создаётся плоское напряжённое состояние, условие прочности которого по энергетической теории имеет вид
Участок СD находится в условиях сложного сопротивления, так как в его сечениях действуют сжимающая продольная сила, изгибающий момент, крутящий момент и поперечная сила (рис. 5), влиянием которой пренебрегаем, и поэтому не показываем. Опасным является сечение D, в котором сочетаются наибольшие значения N, Mx, Mк. Анализ рисунка показывает, что опасной точкой является Е, где суммируются сжимающие нормальные напряжения от продольной силы и изгибающего момента, и одновременно действует касательное напряжение от крутящего момента. Здесь создаётся плоское напряжённое состояние, условие прочности которого по энергетической теории имеет вид
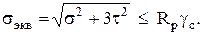 (2)
(2)
Выпишем площадь и моменты сопротивления прямоугольного сечения при изгибе и кручении
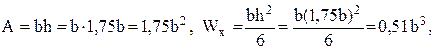
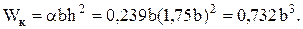
Здесь 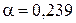 – табличный коэффициент для прямоугольного сечения при
– табличный коэффициент для прямоугольного сечения при 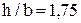 . Нормальное и касательное напряжения в точке Е будут
. Нормальное и касательное напряжения в точке Е будут
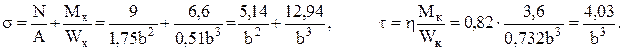
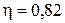 - табличный коэффициент для прямоугольного сечения при
- табличный коэффициент для прямоугольного сечения при 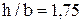 , учитывающий, что точка Е находится в середине короткой стороны прямоугольника.
, учитывающий, что точка Е находится в середине короткой стороны прямоугольника.
Вычислим правую часть условия прочности (2)
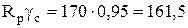 МПа
МПа 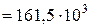 кПа.
кПа.
После подстановок условие прочности (2) принимает вид
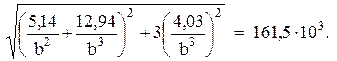 (3)
(3)
Записанное в виде равенства оно представляет собой уравнение с неизвестным b. Определение его корня точными методами затруднительно и требует громоздких преобразований и вычислений. Поэтому применим простой метод итераций (последовательных приближений). С этой целью дробь в подкоренном выражении, содержащую b2, преобразуем, умножив числитель и знаменатель на b.
После несложных преобразований уравнение принимает вид
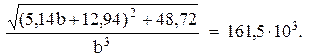 (4)
(4)
Итерационный процесс организуем по формуле, вытекающей из (4)
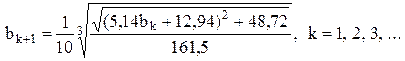 (5)
(5)
Для начала примем, что b1 = 0, и далее проведём вычисления, следуя (5). Итоги счёта в табличной форме
| k | |||||
| b, см | 4,5 | 4,52 | 4,523 | 4,523 |
Вычисления прекращаются, так как заметного уточнения b, уже не происходит. Принимаем, что 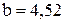 см. Из условия задачи находим второй размер
см. Из условия задачи находим второй размер
h = 1,75b = 1,75·4,52 = 7,91 см.
В середине длинной стороны прямоугольника G касательные напряжения являются наибольшими, поэтому проверим прочность при найденных значениях сечения. Здесь напряжения будут
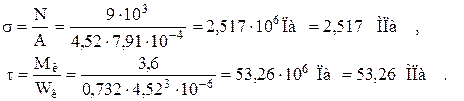
Очевидно, что условие прочности (2) выполняется. Поэтому найденные размеры являются окончательными.
ВАРИАНТЫ ЗАДАНИЙ
| Второе число шифра | 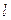 м м | a м | h/b | 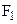 кН кН | 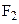 кН кН | M кНм | 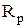 МПа МПа | 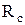 МПа МПа | 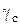 |
| 1,0 | 0,6 | 1,5 | 0,90 | ||||||
| 0,8 | 0,5 | 1,75 | 1,00 | ||||||
| 1,1 | 0,7 | 1,5 | 0,85 | ||||||
| 0,7 | 0,4 | 1,75 | 0,95 | ||||||
| 0,9 | 0,5 | 1,75 | 0,90 |
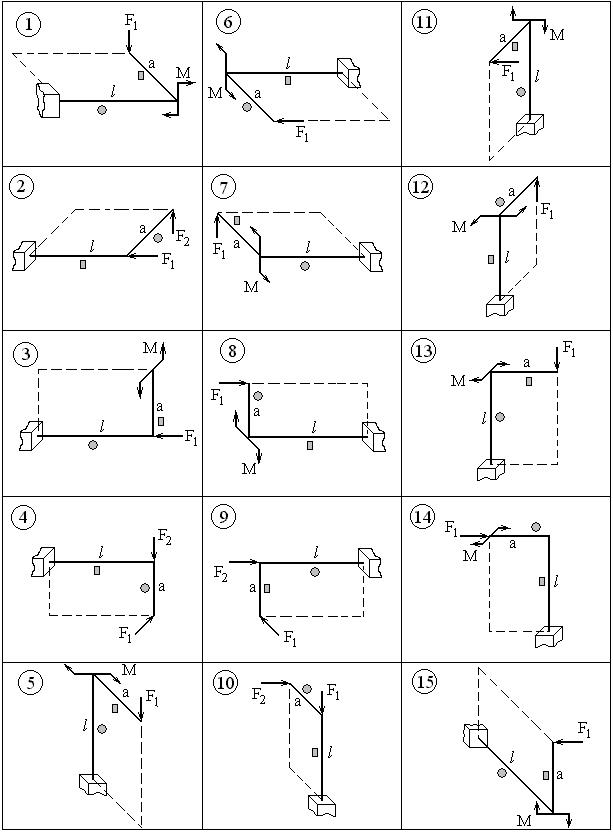 |
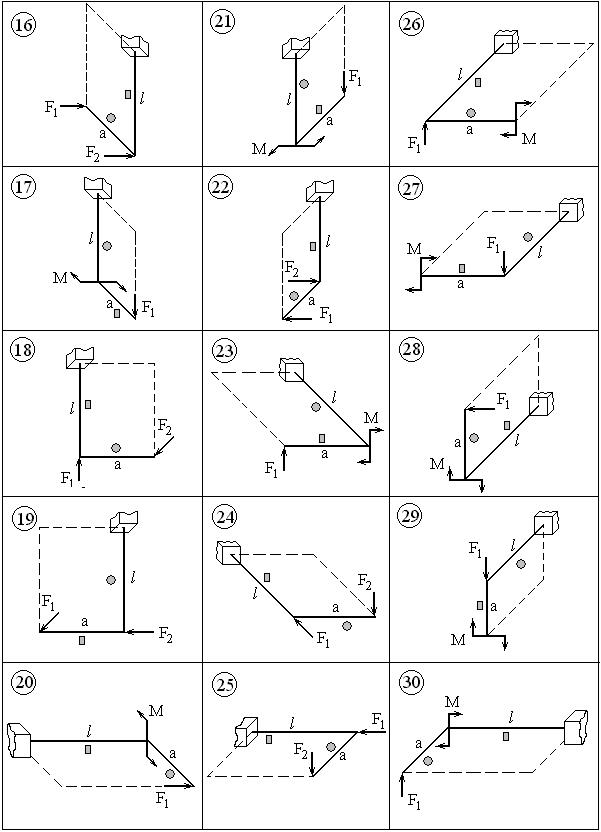 |
Задача 4
