Характеристическая функция течения для кольцевой батареи скважин
Характеристическую функцию для пстоков представим в виде:
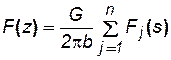. (7.67)
Согласно формуле (7.61), можно записать
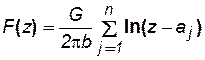. (7.68)
Здесь аj – комплексное число, определяющее положение стока за номером j.
В соответствии с формулой (7.47) комплексное число аj можно представить в тригонометрической форме, заменив в (7.47) z на аj, r на а(радиус батареи). Тогда формулу (7.68) можно переписать для кольцевой батареи из n скважин в следующем виде:
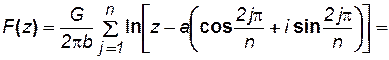(7.69)
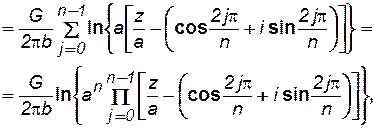
где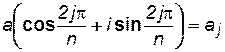 
.
Целая рациональная функция вида хп - 1 может быть представлена в виде
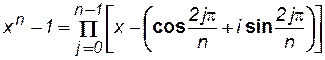. (7.70)
Выражение, сходное с правой частью формулы (7.70) имеется под знаком логарифма в (7.69). Таким образом, можно представить характеристическую функцию F (z)(7.69) в виде:
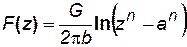. (7.71)
Согласно формулам (7.42) и (7.71) находим модуль массовой скорости фильтрации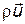 
:
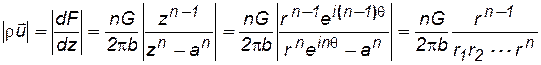, (7.72)
где z = reiq; r1, r2, ..., rn – расстояния точки пласта от стоков O1, О2 , ...Оn– соответственно.
В центре кольцевой батареи r = 0. Из (7.72) следует, что скорость фильтрации u здесь равна нулю. Эти точки фильтрационного поля называются точками равновесия. При разработке залежей нефти в окрестностях таких точек образуются «застойные области» – «целики нефти».
Зная положения точек равновесия в пласте, можно находить рациональные приемы для своевременной ликвидации целиков нефти. Одним из таких приемов является изменение режима работы скважин, заставляющее нефть целика прийти в движение в нужном направлении.
(7.113)
–
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Основные виды задач по заданию режима работы скважин.
2. Сущность метода суперпозиции.
3. Потенциал сложного потока.
4. Уравнения эквипотенциальных поверхностей.
5. Метод отображения источников и стоков.
6. Фильтрационный поток от нагнетательной скважины к эксплуатационной (выражение для потенциала, изобара, поле течения).
7. Фильтрационный поток от нагнетательной скважины к эксплуатационной (выражение для массового дебита, модуль массовой скорости, время и площадь обводнения).
8. Приток к группе скважин с удаленным контуром питания.
9. Приток к скважине в пласте с прямолинейным контуром питания.
10. Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы.
11. Приток к скважине в пласте с произвольным контуром питания.
12. Приток к скважинам кольцевой батареи (дебит скважины и батареи). Что такое – эксцентрично расположенная скважина?
13. Приток к скважинам кольцевой батареи (поле течения, оценки эффекта взаимодействия).
14. Приток к прямолинейной батарее скважин (конечное число скважин). В чем отличие формул Голосова для четного и нечетного числа скважин?
15. Приток к прямолинейной батарее скважин (бесконечное число скважин).
16. Метод Борисова (сущность, внутреннее и внешнее сопротивления).
17. Интерференция несовершенных скважин.
18. Взаимодействие скважин в анизотропном пласте (батарея расположена во внутренней неоднородности кругового пласта).
19. Взаимодействие скважин в неоднородно проницаемом и анизотропном пластах (батарея расположена во внешней неоднородности кругового пласта).
20. Периодически работающая скважина. Уравнение КВД.
21. Влияние радиуса скважины на дебит при взаимодействии скважин.
22. Уравнения Коши-Римана.
23. Потенциальная функция и функция тока.
24. Характеристическая функция течения (комплексный потенциал).
25. Связь проекций массовой скорости с потенциалом и функцией тока.
26. Физический смысл функции тока.
37. Характеристическая функция прямолинейно-параллельного потока.
38. Характеристическая функция плоскорадиального потока.
39. . Характеристическая функция эксценnрично расположенной скважины.
40. . Характеристическая функция группы скважин.
41. . Характеристическая функция источника и стока.
42. Характеристическая функция для кольцевой батареи скважин.