Общие понятия об идеальных циклах двс

Для анализа работы ДВС и определения основных по­казателей (индикаторная мощность, механический к.п.д.) на работающем цилиндре записывают с помощью индикатора индикаторную диаграмму, представляющую собой действитель­ный рабочий процесс в цилиндре двигателя.

Действительный рабочий процесс четырехтактного карбю­раторного ДВС представлен на рис. 1.18.

Такт всасывания. В начале такта поршень находится в ВМТ. Камера сгорания заполнена продуктами сгорания с давлением, превышающим атмосферное. При движении поршня от ВМТ к НМТ открывается всасывающий клапан 2 и цилиндр заполняется топливовоздушной смесью; процесс вса­сывания O - а - т протекает при давлении меньше атмос­ферного.

Такт сжатия. Поршень перемещается от НМТ к ВМТ;

находящаяся в цилиндре топливовоздушная смесь (всасываю­щий 2 и выхлопной / клапаны закрыты) сжимается по политропе т - с. Давление в конце сжатия (точка с) в карбюраторных ДВС достигает 1,0... 1,5 МПа, температура 500...650 К. Этих параметров недостаточно для самовоспла­менения смеси, поэтому до прихода поршня в ВМТ (угол опережения зажигания) в цилиндр подается электрическая искра.

Такт расширения. Рабочая (горючая) смесь у карбюра­торных ДВС сгорает практически при постоянном объеме (линия с - г). В. точке г давление в цилиндре достигает 3,0...5,0 МПа, а температура 2000...2500 К. Расширяясь (линия г — — b), продукты сгорания перемещают поршень от ВМТ к НМТ, совершая при этом механическую работу, которая в виде крутящего момента передается маховику.

Такт выхлопа отработавших газов. Поршень движется от НМТ к ВМТ; процесс происходит по линии - b - 0 при давлении 0,105...0,115 МПа, т.е. несколько выше атмосферного, а температура выхлопных газов достигает 900... 1000 К.

Далее все процессы повторяются. Таким образом, рабочий процесс четырехтактного ДВС осуществляется за четыре хода поршня, т.е. за два оборота коленчатого вала.

Рассмотренный рабочий процесс реального ДВС протекает при потере теплоты, трении, реакции горения топлива и пере­менной массе газов. Это затрудняет анализ работы ДВС с точки зрения термодинамики. В связи с этим рабочие процес­сы реальных ДВС заменяют идеальными циклами, которые отличаются введением следующих упрощений:

считается, что в цикле участвует одно и то же количе­ство рабочего тела (1 кг);

2) считается, что теплота 171 подводится от горячего источ­ника, а не является результатом химических реакций (сгора­ния), происходящих внутри цилиндра двигателя;

3) не учитываются потери в окружающую среду, а учиты­вается только одна основная потеря теплоты 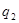, и процессы сжатия и расширения принимаются адиабатными;

4) все процессы цикла принимаются равновесными, обрати­мыми.

Для того, чтобы результаты исследования идеальных циклов можно было перенести на действительные рабочие процессы, в расчеты вводят опытные коэффициенты.

По способу подвода теплоты к рабочему телу различают три идеальных цикла ДВС: при v = idem; при р = idem; при v = idem и р = idem или цикле со смешанным подводом теплоты.

Идеальный цикл ДВС с подводом теплоты при постоян­ном объеме v = idem является теоретической основой действи­тельного рабочего процесса карбюраторного двигателя. Цикл состоит из двух адиабатных и двух изохорных термодинами­ческих процессов. Графическое изображение идеального цикла в

pv- и Ts -диаграммах приведено на рис. 1.19 и 1.20.

Состояние рабочего тела изменяется следующим образом. При перемещении поршня справа налево газ (рабочее тело) сжимается по адиабате 1-2, в результате объем его уменьшает­ся от .

Отношение начального объема к конечному называется степенью сжатия :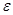

Степень сжатия определяет значение термического к.п.д. цикла, ограничивается в карбюраторных ДВС самовоспламене­нием топливовоздушной смеси и не превышает 9...10.

Работа сжатия в адиабатном процессе 1-2, как указывалось ранее, отрицательна.

В изохорном процессе 2 — 3 к рабочему телу подводится теплота 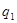, эквивалентная теплоте, выделяющейся при сгора­нии топлива:

По адиабате 3-4 газ расширяется до объема , совершая при этом положительную работу. Результирующая работа цикла равна разности работ адиабатных процессов расширения и сжатия и изображается на pv-диаграмме площадью цикла 1-2-3-4-1.

В изохорном процессе 4 - 1 от рабочего тела отводится теплота .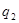

Полезно используемая теплота в цикле равна разности подводимой и отводимой теплоты:

На Ts-диаграмме (см. рис. 1.20) теплота изображается площадью 1-2-3-4.

Найдем по общему уравнению термический к.п.д. цикла:

После выполнения необходимых преобразований получим следующую расчетную формулу:

Из данной формулы видно, что 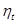, цикла ДВС с подводом теплоты при v = idem возрастает при увеличении степени сжатия 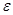и зависит от физических свойств рабочего тела (коэффициент k) (рис. 1.21).

В идеальном цикле ДВС с подводом теплоты при по­стоянном давлении

( р = idem) сжимается не топливо- воздушная смесь, а воздух, поступающий из атмосферы. Для повышения термического к. п. д. в двигателях этого типа применяют высокие степени сжатия ( 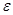= 14...20). Поэтому в цилиндре двигателя в конце сжатия давление воздуха составляет от 4,0 до 4,8 МПа, а температура достигает 900 , что значительно превышает температуру самовоспламенения впрыскиваемого распыленного топлива. Цикл предложен в 1897 г. инженером Дизелем и носит его имя. Жидкое топливо при реальном цикле распыливается воздухом, сжатым специальным компрессором.

Данный цикл в pv- и Ts-диаграммах показан на рис. 1.22 и 1.23.

В этом цикле рабочее тело из начального состояния 1 адиабатно сжимается (кривая 1- 2) до объема точке 2. Степень сжатия

В изобарном процессе 2-3 подводимую теплоту 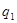можно вычислить по уравнению

Отношение объема (в точке 3) к объему (в точке 2) называется степенью предварительного расширения и обозна­чается :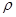

Дальнейшее расширение рабочего тела осуществляется по адиабате ( = idem) 3 - 4, а в изохорном процессе 4 - 1 отводится теплота :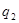

Термический к. п. д. цикла определяется из общего выра­жения

После несложных преобразований получаем окончательное выражение термического к. п. д. рассматриваемого цикла:

Из данного уравнения следует, что т), тем выше, чем больше степень сжатия 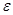и чем меньше степень предварительного рас­ширения 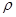(рис. 1.24).

3. Идеальный цикл ДВС со смешанным подводом теплоты (при v = idem и p = idem) лежит в основе работы всех со­временных бескомпрессорных дизелей. Этот цикл предложен в 1904 г. русским инженером Г.В. Тринклером и называется циклом Тринклера. В ДВС, работающих по данному циклу, как и в предыдущем случае (в цикле с подводом теплоты при p = idem), в цилиндре сжимается воздух, поэтому допускаются те же степени сжатия 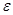≈ 14... 20. В pv- и Ts-координатах цикл изображен на рис. 1.25 и 1.26.

Отношение давления к давлению называется степенью повышения давления и обозначается :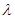

Термический к. п. д. цикла определяется из выражения

После подстановки в данную формулу выражений для и выполнения необходимых преобразований получим расчетное уравнение термического к.п.д. в виде

Из этого выражения видно, что термический к.п.д. цикла повышается с увеличением степени сжатия 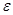и степени повышения давления λ; увеличение степени предварительного расширения ρ отрицательно влияет на значение термического к.п.д.Сравнение экономичности рассмотренных выше идеальных циклов ДВС при одинаковых параметрах рабочего тела в конце процессов подвода теплоты, т.е. , показывает, что термический к.п. д. идеального газа цикла ДВС с подводом теплоты при p = idem теоретически несколько больше, чем в идеальном цикле со смешанным подводом теплоты, и значительно больше, чем в цикле с подводом теплоты при v = idem:

Это положение наглядно показано на рис. 1.27. При одинаковом значении е (рис. 1.28)

ОСНОВЫ ТЕПЛООБМЕНА

ТЕПЛОПРОВОДНОСТЬ

ТЕМПЕРАТУРНОЕ ПОЛЕ

Процесс теплопроводности, как и другие виды теплообмена, может иметь место только при наличии разности температур согласно второму закону термодинамики. В общем случае этот процесс сопровождается изменением температуры как в пространстве, так и во времени. Поэтому исследование теплопроводности сводится к изучению пространственно-временного изменения температуры, т.е. к нахождению уравнения

Уравнение (2.1) представляет собой математическое вы­ражение температурного поля. Следовательно, температур­ное поле есть совокупность значений температуры во всех точках изучаемого пространства для каждого момента времени. Различают стационарное и нестационарное темпе­ратурные поля. Уравнение (2.1) является записью наиболее общего вида температурного поля, когда температура изменяет­ся с течением времени и от одной точки к другой. Такое поле отвечает неустановившемуся тепловому режиму теплопровод­ности и носит название нестационарного (неустановившегося) температурного поля.

Если тепловой режим установившийся, то температура в каждой точке пространства с течением времени остается неизменной, и такое температурное поле называется стацио­нарным (установившимся). В этом случае температура являет­ся функцией только координат и не зависит от времени:

Температурное поле, соответствующее уравнениям (2.1) и (2.2), трехмерное, так как температура является функцией трех координат, однако она может изменяться в зависимости от одной, двух или трех координат. В соответствии с этим различают одномерные, двухмерные и трехмерные температур­ные поля - как стационарные, так и нестационарные.

Наиболее простой вид имеет уравнение одномерного стационарного температурного поля: