Формы записи задачи линейного программирования и методы решения

Классификация задач оптимального программирования

Задачи оптимального программирования в наиболее об­щем виде классифицируют по следующим признакам.

1. По характеру взаимосвязи между переменными:

а) линейные,

б) нелинейные.

В случае а) все функциональные связи в системе ограни­чений и функция цели — линейные функции; наличие не­линейности хотя бы в одном из упомянутых элементов при­водит к случаю б).

2. По характеру изменения переменных:

а) непрерывные,

б) дискретные.

В случае а) значения каждой из управляющих перемен­ных могут заполнять сплошь некоторую область действи­тельных чисел; в случае б) все или хотя бы одна переменная могут принимать только целочисленные значения.

3. По учету фактора времени —

а) статические,

б) динамические.

В задачах а) моделирование и принятие решений осуще­ствляются в предположении о независимости от времени элементов модели в течение периода времени, на который принимается планово-управленческое решение. В случае б) такое предположение достаточно аргументировано принято не может быть, и необходимо учитывать фактор времени.

4. По наличию информации о переменных —

а) задачи в условиях полной определенности (детерминированные),

б) задачи в условиях неполной информации,

в) задачи в условиях неопределенности.

В задачах б) отдельные элементы являются вероятност­ными величинами, однако известны или дополнительными статистическими исследованиями могут быть установлены их законы распределения. В случае в) можно сделать пред­положение о возможных исходах случайных элементов, но нет возможности сделать вывод о вероятностях исходов.

5. По числу критериев оценки альтернатив —

а) простые, однокритериальные задачи,

б) сложные, многокритериальные задачи.

В задачах а) экономически приемлемо использование од­ного критерия оптимальности или удается специальными процедурами (например, «взвешиванием приоритетов») све­сти многокритериальный поиск к однокритериальному.

Сочетание признаков классификации 1—5 позволяет группировать (клас­сифицировать) в самом общем виде задачи и методы опти­мального программирования, например:

1а)2а)3а)4а)5а) — задачи и методы линейного программирования;

1б)2а)3а) 4а)5а) — задачи и методы нелинейного программирования;

1а)2б)3а)4а)5а) — задачи и методы целочисленного (дис­кретного) линейного программирования и т.д.

Формы записи задачи линейного программирования и методы решения

Как отмечено выше, среди широкого класса задач опти­мального программирования имеются важные подклассы за­дач, для которых разработаны эффективные методы реше­ния. Наиболее изученным подклассом задач являются зада­чи линейного программирования.

В задаче линейного программирования (ЗЛП) требуется найти экстремум(максимум или минимум) линейной целе­вой функции

f (x) :

max (min) f ( x ) = c₁*x₁+c₂*x₂+……….+c_n*x_n (9)

при ограничениях (условиях):

a₁₁*x₁+a₁₂*x₂+…….+a_1n*x_n {£, =, ³} b₁,

a₂₁*x₁+a₂₂*x₂+…….+a_2n*x_n {£, =, ³} b₂, (10)

………………………………………….

a_m1*x₁+a_m2*x₂+…….+a_mn*x_n {£, =, ³} b_m,

X_j ³ 0, j = 1, n , (11)

где a_ij, b_i, c_j (i=1,m , j=1, n ) – заданные постоянные величины.

1) Так записывается общая задача линейного программирования в развернутой форме.

Знак {£, =, ³} означает, что в конкретной ЗЛП возможно ограничение типа равенства или неравенства (в ту или иную сторону).

Систему ограничений (10) называют функциональными ограничениями ЗЛП, а ограничения (11) – прямыми ограничениями.

Вектор X= (x₁, x₂,…., х_п), удовлетворяющий системе ог­раничений (10) и (11), называется допустимым решением, или планом ЗЛП, т.е. ограничения (10)- (11) определяют область допустимых решений, или плановзадачи линей­ного программирования (область определения ЗЛП).

План (допустимое решение), который доставляет максимум или минимум целевой функции (9), называется опти­мальным планом (оптимальным решением) ЗЛП.

2) Канонической формой записи задачи линейного програм­мирования (КЗЛП) называют задачу вида (запись с исполь­зованием знаков суммирования):

Найти: max f ( X) = 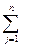C_j *X_j (12)

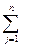при ограничениях: a_ij *X_j = b_i , i =1, m , (13)

X_j ³ 0, j= 1, n. (14)

Приведение ЗЛП к каноническому виду осуществляется введением в левую часть соответствующего ограничения вида (10) k-тойдополнительной переменной X_n+k ³ 0 со знаком “ - “ в случае ограничения типа “³” b и знаком “+” в случае ограниче­ния типа “£”.

Если на некоторую переменную х_r не накладывается ус­ловие неотрицательности, то делают замену переменных х_r = х'_r - х" _r, х' _r ³ 0, х"_r ³0. В преобразованной задаче все переменные неотрицательные. Переход к задаче на макси­мум достигается изменением в случае необходимости знака у целевой функции.

3) Векторная форма записи ЗЛП имеет вид:

Найти: max (min) f(X)=C*X

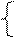при ограничениях: A₁₁ *x₁+ A₂₂ *x ₂+ ... + А_n*х_n {£, =, ³} В(b₁,b₂,…,b_n),

х_j ³0,

где С = (c₁,с₂, ...,с_n)-вектор-строка;Х = (х_1,х₂,...,х_n) – вектор-столбец;

С*Х — скалярное произведение векторов С,Х; Ajи В — вектор-столбцы:

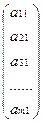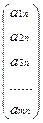A₁ = , A₂= , ….., A_n= , B =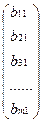

4) Матричная форма записи ЗЛП:

max (min) f(X) =C*X

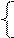при условиях: A*X{£, =, ³} B

X ³ 0

Здесь С = (с₁,с₂,….,с_n) –вектор-строка; A= (a_ij ) – матрица размерности m ´n, столбцами которой являются вектор-столбцы A_j.

X = 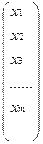- вектор-столбец, B = 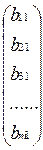- вектор-столбец.

5) Стандартная форма записи ЗЛП:

max (min) f (X) =C * X ,

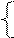
A*X {£, =, ³} B,

X ³ 0.

При этом запись X ³ 0 понимают как вектор ( или вектор-столбец в зависимости от контекста), у которого все компоненты (элементы) неотрицательны.

К математическим задачам линейного программирова­ния приводят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде ин­терпретируются как задачи об оптимальном использова­нии ограниченных ресурсов (задача об оптимизации производственной программы предприятия, задача об оптимальном использовании производственных мощностей, оптимизация состава промышленных смесей и раскроя материала, оптимизация перевозок и т.д.