Тестовые задания для самостоятельного решения
ТЗ 1. Легкое. В урне 5 белых, 3 черных и 2 красных шара, из которых извлекают 3. Вероятность того, что все они красные, равна…
а) £ 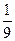
б) £ 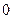
в) £ 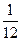
г) £ 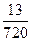
д) £ 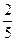
ТЗ 2. Средней трудности. Наугад выбирается двузначное число. Вероятность того, что в нем не содержится цифры 9, равна…
а) £ 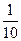
б) £ 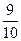
в) £ 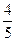
г) £ 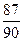
д) £ 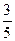
ТЗ 3. Трудное. В урне 5 белых, 3 черных и 2 красных шара, из которых извлекают 3. Вероятность того, что все они разных цветов, равна…
а) £ 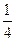
б) £ 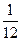
в) £ 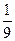
г) £ 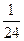
д) £ 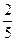
ТЗ 4. Повышенной трудности. В стопке 10 тетрадей. Из них 6 в клетку, остальные в линию. Из стопки наугад выбирают сразу две тетради. Вероятность того, что они обе в клетку, равна …
а) £ 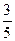
б) £ 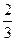
в) £ 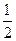
г) £ 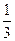
д) £ 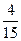
ТЗ 5. Средней трудности. Двое договариваются о встрече в определенном месте, которая должна произойти в промежутке времени от 4 часов до 4 часов и 20 минут. Каждый из договаривающихся приходит к месту встречи в любой наугад взятый момент времени из этого промежутка времени и ждет другого 4 минут (в пределах указанного промежутка времени). Вероятность, что встреча состоится равна ...
а) £ 1/5
б) £ 1/9
в) £ 1/36
г) £ 1/15
д) £ 9/25
Тема 2. Комбинаторика. Бином Ньютона
Основные определения
Определение 2.1.Число сочетаний. Если требуется выбрать k объектов из n имеющихся, с учетом их порядка, для расчета количества способов выбора удобно пользоваться формулой числа сочетаний 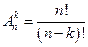 .
.
Определение 2.2.Число 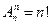 определяет количество перестановок из n объектов.
определяет количество перестановок из n объектов.
Примеры решения тестовых заданий
Определение 2.3.
Пример 5.Дано 4 точки. Число прямых, которые можно провести через них, если известно, что никакие три из этих точек не лежат на одной прямой, равно…
Решение 5.Есть два способа решения этой задачи. Первый способ заключается в том, чтобы непосредственно сосчитать все варианты. Для того чтобы провести прямую требуется две точки. Мысленно перенумеруем точки числами от 1 до 4. Выберем в качестве первой точки точку номер 1. Существует три прямые, которые можно провести через данную точку – это прямые 1-2, 1-3, 1-4. Теперь выберем в качестве первой точки точку номер 2. Есть две прямые, которые через нее проходят и отличаются от предыдущих 3-х – это прямые 2-3 и 2-4 (прямая 2-1 уже была). И, наконец, если выбрать в качестве первой точки точку номер 3, останется только одна прямая – 3-4. В итоге, ответ 3 + 2 + 1 = 6. Второй способ основан на использовании числа комбинаций 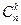 (Определение 1.11), поскольку порядок выбора точек не важен. Ответ
(Определение 1.11), поскольку порядок выбора точек не важен. Ответ 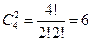 .
.
Пример 6.Количество двузначных чисел, составленных из цифр 1, 2, 3, 4, 5 при условии, что каждая цифра в нем встречается только один раз, равно ...
Решение 6.Первый способ решения – это непосредственный подсчет. В двузначном числе имеется два разряда. В первом разряде может стоять одна из пяти имеющихся цифр, поэтому перебирая их, мы получим 5 различных двузначных чисел. Перейдем ко второму разряду. Поскольку одна из цифр у нас уже занята под первый разряд, остается 4 варианта заполнения второго разряда. На каждый вариант заполнения первого разряда имеется 4 варианта заполнения второго. Итого получаем 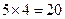 различных двузначных чисел. Второй способ решения использует число сочетаний
различных двузначных чисел. Второй способ решения использует число сочетаний 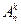 (Определение 2.1), т.к. порядок цифр в числе важен. Ответ
(Определение 2.1), т.к. порядок цифр в числе важен. Ответ 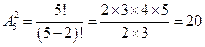 .
.
Пример 7.Количество способов выбора из 6 человек группы людей для работы, если группа должна состоять не менее чем из 5 человек, равно ...
Решение 7.Не менее чем 5 означает, что для работы требуется выбрать 5 или 6 человек. 5 человек из 6 можно выбрать шестью способами (есть 6 вариантов оставить одного человека) и 6 человек из 6 можно выбрать только одним способом. Ответ 6 + 1 = 7.
Пример 8.Количество таких шестизначных чисел, которые начинаются с цифры 1, заканчиваются на 0, а все остальные их цифры различны и не меньше 5, равно…
Решение 8.В шестизначном числе по условию задачи имеется четыре незанятых разряда. Цифры «не меньшие 5» – это 5, 6, 7, 8, 9. Действуя по аналогии с примером 6, сразу получаем ответ 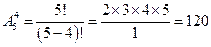 .
.
