ПФ систем в пространстве состояний

Ранее была рассмотрена математическая модель системы без учета внутреннего состояния Х объекта управления, а ПФ системы описывала взаимосвязь только входных и выходных сигналов. Это описание называется внешним.

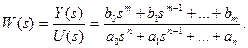(2.4)

Преимуществом данного метода описания заключается в том, что, используя комплексные переменные, можно применять алгебраические методы. Полагая при этом, что начальные значения переменных состояния Х – нулевые.

Дифференциальные уравнения, описывающие технологический процесс, всегда можно преобразовать к системе обыкновенных дифференциальных уравнений первого порядка. В этом случае говорят, что это описание в виде уравнений состояния или в пространстве состояний. Управляемую систему можно представить в виде общей модели

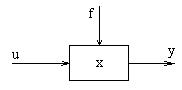
Рисунок 2.6 – Блок-схема системы: u – вектор входного сигнала управления; f – вектор входного сигнала возмущения; х – вектор состояния; у – вектор выходного сигнала

Описание системы, учитывающая взаимосвязь входных и выходных сигналов через состояние объекта управления Х , называется внутренним. Основным достоинством данного метода является возможность использования численного метода интегрирования (Эйлера, Рунге Кутта и т.д.) для решения дифференциальных уравнений.

Математическим аппаратом моделей в пространстве состояний является линейная алгебра: операции с векторами и матрицами. Если известны входные сигналы управления u = (u₁ u₂ ...u_r)^T и возмущения f = (f₁ f₂ ...f_m)^T, текущее состояние системы x = (x₁ x₂ ...x_n)^T, то можно предсказать ее дальнейшее поведение, т.е. рассчитать выходной сигнал у = (у₁ у₂ …у_р)^Т, где буква Т означает матрицу-столбец.

В матричном виде уравнение состояния системы записывается как

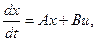(2.5)

или

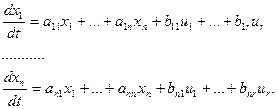
Матрицы коэффициентов А размерностью (nxn) и В размерностью (nxr) равны

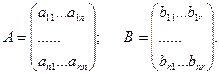
При единственном входном сигнале, например, управляющем u = u₁ матрица В имеет только один столбец

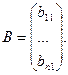
Между внутренними состояниями, сигналом управления и выходным сигналом существует зависимость

y = C x + D u, (2.6)

где С и Д матрицы коэффициентов размерностью (pxn) и (pxr) соответственно и равные

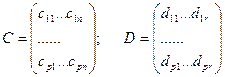
или

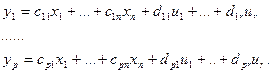
Если в системе имеется один выход у = у₁ , то матрица С состоит только из одной строки С = (с₁ …с_n), а матрица Д – нулевая.

ПФ системы можно рассчитать непосредственно из внутреннего описания в переменных состояния, используя формулы (2.5) и (2.6). Для этого представим уравнение (2.5) в изображениях Лапласа

pEx(p) = Ax(p) + Bu(p),

где Е – единичная матрица размерностью (nxn); р = d/dt – оператор Лапласа.

Тогда вектор состояния будет равен

x(p) = (pE - A)^-1Bu.

Подставив х(р) в формулу (4.6) выраженное через изображения Лапласа, получим выходной сигнал

y(p) = C(pE – A)^-1 Bu(p) + Du(p).

Тогда ПФ системы будет равна

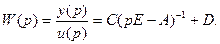(2.7)

Знаменатель ПФ называется характеристическим уравнением, корни которого называются полюсами (poles). Значения полюсов идентичны собственным числам матрицы А. Корни числителя называются нулями (zeros). Если нули обозначить z₁, ..., z_m, а полюса – p₁,..., p_n, то при n > m ПФ формулы (4.4) можно записать в виде

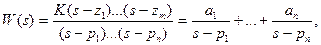
где а_i – действительные или комплексные константы.

Это означает, что выходную переменную у можно представить суммой показательных функций (с помощью таблиц обратных переходов Лапласа), которые называются модами

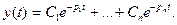
Моды зависят от входного управляющего сигнала u(t). Вещественный полюс соответствует слагаемому с вещественным показателем степени, а два комплексно-сопряженных полюса всегда можно представить в виде одного слагаемого. Действительно, если два полюса имеют значения 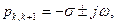то этой паре соответствует одно слагаемое

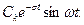
Полюса или собственные числа матрицы А линейной системы полностью определяют устойчивость. Если вещественные части полюсов – отрицательные (лежат в левой части комплексной плоскости или просто левые), то реакция на ограниченный (например, единичный) входной сигнал u(t) всегда также ограниченна, т.е. система устойчива.

Нули определяют значения коэффициентов экспоненциальных функций С₁ … С_n , но не влияют на устойчивость системы. Если полюс располагается ближе к нулю, то соответствующая мода мала. Если полюс и нуль совпадают, то мода исчезает.