Расчеты статической ошибки εСТ регулирования 9 страница

,

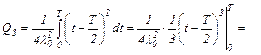
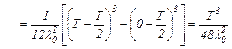откуда находим

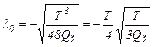
Окончательно оптимальные законы изменения частоты вращения и тока якоря примут вид

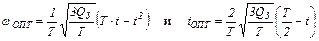(5.17)

Графики сигналов ω_ОПТ при i_ОПТ оптимальном управлении приведены на рис.5.2.

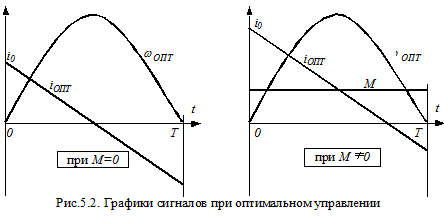
Традиционно применяют разгон и торможение при постоянном токе якоря ДПТ (рис.5.3). За время Т при заданном значении Q_З поворот α вала составляет

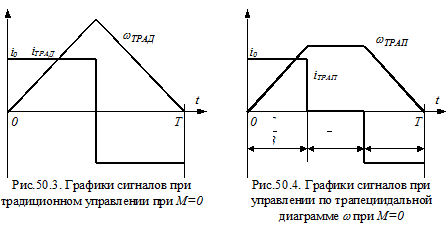
всего лишь 75% от поворота при оптимальном управлении. Если же сравнивать оптимальное и традиционное управление ДПТ при условии, что в обоих случаях за время Т вал повернется на одинаковый угол α, то тепловыделения при традиционном управлении превысят тепловыделения при оптимальном управлении на 33%.

Близкое к оптимальному является управление по трапециидальной диаграмме частоты вращения ω (рис.5.4). Различие в угле поворота α составляет всего 12%.

С увеличением момента М сопротивления нагрузки различия в значениях α и Q становятся всё меньшими.

Вопросы и задания

1. Сформулируйте постановку задачи оптимального управления ДПТ при М_С=const: определите функционал и ограничения.

2. Как ищется решение задачи оптимального управления ДПТ ?

3. Как определяются постоянные величины, входящие в решение ?

4. Какая эффективность оптимального управления в сравнении с традиционными управлениями ДПТ ?

5.3. Оптимальное управление ДПТ с независимым возбуждением при ограничениях на частоту вращения и ток якоря

Ограничения на частоту вращения и ток якоря должны учитываться для любого электродвигателя.

1. Ограничение на частоту вращения.

К функционалу вида (5.8), уравнению связи вида (5.9) и ограничению вида (5.10) добавляется еще одно ограничение

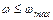(5.18)

Вначале вариационным методом ищется решение, которое будет иметь вид (5.13), а после определения постоянных интегрирования С₁ и С₂ - вид (5.17). Далее строится график ω_ОПТ и на нем определяется максимальное значение ω. Если неравенство (5.18) не нарушается, то поставленную задачу можно считать решенной. График ω_ОПТ будет таким же, каким он изображен на рис.5.2.

Если неравенство (5.18) нарушается, то оптимальный закон изменения частоты вращения ω будет состоять и участков экстремалей вида (5.13) и граничных участков с предельной частотой ω=ω_max. В точках склеивания экстремалей и граничных участков должны выполняться условия Вейерштрасса-Эрдмана: значения производных к склеиваемым линиям в точках склеивания должны совпадать. Так как для участков с ω=ω_max производная 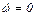, то в точках склеивания производные для линий типа (5.13) должны быть равны нулю. Экстремали (5.13) являются параболами (рис.5.2) и точка, в которой 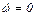, совпадает с вершиной параболы. График ω_ОПТ будет иметь вид, показанный на рис.5.5, на котором параболические и линейный участки склеены в вершинах парабол. Там же показан график оптимального закона изменения тока якоря i_ОПТ, который на интервалах времени 0,5·Т_е, на которых график ω_ОПТ является графиком экстремалей, изменяется по закону (5.14), на интервалах времени, в которых ω_ОПТ=ω_max, ток якоря постоянный, причем в соответствии с уравнением связи (5.9) величина этого тока равна моменту нагрузки М.

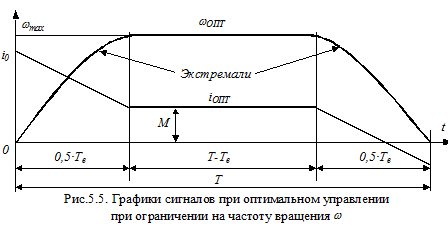
График 1-й экстремали (при t=0...0,5T_e) и график тока описываются подобно (5.16) выражениями

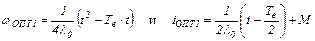
График 2-й экстремали (при t=Т...Т-0,5T_e) сдвинут вправо относительно первой на время Т-Т_е (на рис.5.5 показан такой величины сдвиг вершин парабол) и, поэтому, описание 2-й экстремали получается заменой t на t-(T-T_e)=t-T+T_e в описании 1-й экстремали. Такую же замену нужно сделать и в выражении тока.

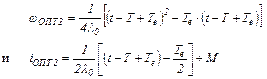
Из выражения ω_ОПТ при значении t=0,5T_e,определяем максимальное значение частоты вращения ω_max

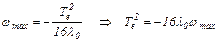
Количество выделившегося тепла, которое должно быть равно заданному Q_З, определяется выражением

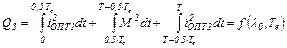
Из системы двух уравнений

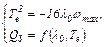
определяются значения λ₀ и Т_е и этим полностью решается задача расчета параметров графика ω_ОПТ, составленного из кусков экстремалей и граничного участка с ω=ω_max (рис.5.5).

2. Ограничение на ток якоря

К функционалу вида (5.8), уравнению связи вида (5.9) и ограничению вида (5.10) добавляется еще одно ограничение

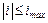(5.19)

Вначале вариационным методом ищется решение, которое будет иметь вид (5.13), а после определения постоянных интегрирования С₁ и С₂ - вид (5.17). Далее строится графики ω_ОПТ и i_ОПТ. На графике i_ОПТ определяется максимальное значение. Если неравенство (5.19) не нарушается, то поставленную задачу можно считать решенной. Графики ω_ОПТ и i_ОПТ будут такими же, какими изображены на рис.5.2.

Если неравенство (5.19) нарушается, то оптимальный закон изменения частоты вращения ω будет содержать участки с линейно изменяющейся частотой вращения, так как при i=±i_тах и М=const согласно (5.9) переменная ω изменяется с постоянной скоростью. На интервалах времени, где ограничение (5.19) не нарушается, график ω_ОПТ будет состоять из экстремали вида (5.13). В точках склеивания экстремалей и граничных участков с 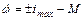должны выполняться условия Вейерштрасса-Эрдмана: значения производных к линиям в точках склеивания должны совпадать.

График ω_ОПТ будет иметь вид, показанный на рис.5.6.

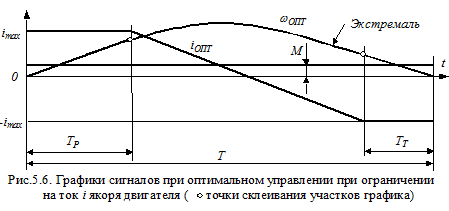
Основная сложность расчетов графика ω_ОПТ состоит в определении длительностей периода разгона Т_Р двигателя при постоянном токе i=+i_тах и периода торможения Т_Т при постоянном токе i=-i_тах.

Вопросы и задания

1. Каким будет решение, если не нарушены ограничения на величину тока якоря и на максимальную частоту вращения ?

2. Каким будет решение, если не нарушены ограничения на величину тока якоря, а частота вращения могла бы превысить максимальную ?

3. Каким будет решение, если не нарушены ограничения на максимальную частоту вращения, тока якоря мог бы превысить максимальное значение ?

5.4. Оптимальное управление ДПТ с независимым возбуждением при моменте сопротивления, зависящем от частоты вращения и времени

1. Момент сопротивления зависит от частоты вращения

Примером электропривода, момент сопротивления которого зависит от частоты вращения, является электропривод траловой лебедки. Сила натяжения ваеров пропорциональна скорости v выборки трала (F=F₀+kv^1,5) и, следовательно, момент сопротивления на валу двигателя пропорционален его частоте вращения (M=M₀+kω^1,5).

Ставится задача нахождения оптимального графика ω_ОПТ частоты вращения ω, доставляющего максимум функционалу (5.8) при ограничении (5.10) и уравнении связи (5.9), в котором М зависит от ω.

Уравнение Эйлера (по переменной ω) от расширенной функции (5.11) и его решение:

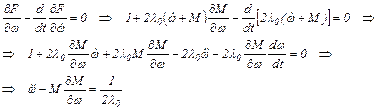
Умножим обе части последнего уравнения на 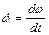и выполним преобразования:

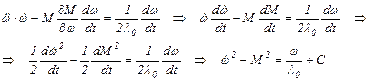
Получен универсальный результат

,

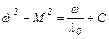который связывает момент М и частоту вращения ω ДПТ при любой функциональной зависимости между ними, а не только той, которая существует для электропривода траловой лебедки.

В частности, для электропривода траловой лебедки оптимальный закон изменения частоты вращения ω при M=M₀+kω^1,5 удовлетворяет следующему дифференциальному уравнению

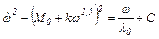
Решением этого дифференциального уравнения является график ω_ОПТ.

Оптимальный график тока якоря двигателя имеет вид

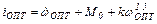
2. Момент сопротивления зависит от времени

Примером электропривода, момент сопротивления которого зависит от времени, является электропривод якорно-швартовного устройства. Для этого электропривода момент сопротивления уменьшается по линейной зависимости от времени M=M₀+kt выборки цепи якоря.

Ставится задача нахождения оптимального графика ω_ОПТ частоты вращения ω, доставляющего максимум функционалу (5.8) при ограничении (5.10) и уравнении связи (5.9), в котором М зависит от t.

Уравнение Эйлера (по переменной ω) от расширенной функции (5.11) и его решение:

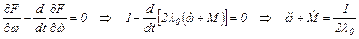
При моменте сопротивления, линейно изменяющемся во времени M=M₀+kt, дифференциальное уравнение оптимального управления имеет вид

,

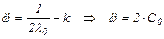решением которого является параболическая функция

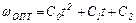(5.20)

С учетом уравнения связи 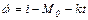оптимальный график для тока якоря является линейным

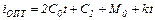(5.21)

В целом оптимальное управление получилось по форме таким же, как и для электропривода с постоянным моментом сопротивления - выражения (5.20) и (5.21) подобны выражениям (5.13) и (5.14).

Вопросы и задания

1. Какой является экстремаль в решении задачи оптимального управления ДПТ с моментом сопротивления нагрузки зависящем от частоты ?

2. Какое управление ДПТ электропривода траловой лебедки в режиме выборки трала является оптимальным ?

3. Какое управление ДПТ электропривода якорно-швартовного устройства в режиме подъема якоря является оптимальным ?

5.5. Оптимальное управление ДПТ с независимым

возбуждением при моменте сопротивления,

зависящем от угла поворота вала

Примером электропривода, момент сопротивления которого зависит от угла поворота вала, является электропривод руля. График механической характеристики руля имеет в первом приближении вид, изображенный на рис.5.7.

Функционалом является время Т поворота руля на заданный угол α_ЗР

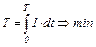(52.1)

Уравнением связи является уравнение динамики электропривода

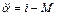(5.22)

Ограничениями являются заданное количество тепла, выделившееся в обмотке якоря за время Т,

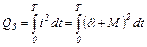(5.23)

и заданный угол поворота вала двигателя, который пропорционален заданному углу поворота руля α_ЗР,

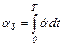
Расширенная функция

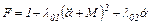
Уравнение Эйлера-Пуассона (по переменной α) от расширенной функции и его решение

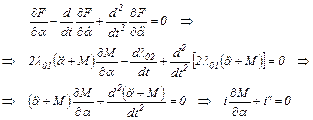(5.24)

Механическая характеристика руля, приведенная на рис.5.7, описывается выражением

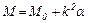(5.25)

После подстановки (5.25) в последнее уравнение цепи (5.24) получим дифференциальное уравнение для определения оптимального графика тока якоря двигателя

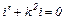(5.26)

Решение уравнения (5.26) имеет вид

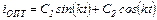(5.27)

Оптимальный график для угла поворота α_ОПТ согласно (5.22) с учетом (5.25) и (5.27) определяется из следующего дифференциального уравнения

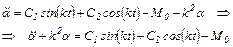(5.28)

Ищем решение последнего дифференциального уравнения цепи (5.28) как сумму свободного α_СВ и принужденного α_ПР решений.

Свободное решение, найденное с учетом характеристического уравнения дифференциального уравнения (5.28), имеет вид

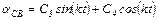
Принужденное решение, учитывающее вид правой части дифференциального уравнения (5.28), будет следующим

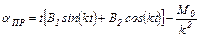(5.29)

Для определения коэффициентов В₁ и В₂ подставим (5.29) в (5.28)

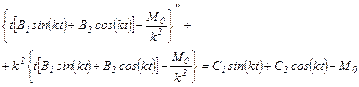(5.30)

После преобразований, выполненных над (5.30), получено

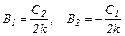
Полное решение дифференциального уравнения (5.28) имеет вид

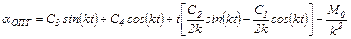
Для определения четырех постоянных интегрирования С₁...С₄ и времени Т нужно составить систему из пяти уравнений:

- два уравнения из граничных условий для угла α:

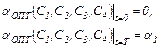
- два уравнения из условий неподвижности руля в начале и конце движения:

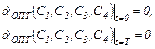
- одно уравнение как результат вычисления интеграла (5.23):

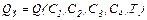
Найденные таким образом постоянные интегрирования С₁ и С₂ нужно также поставить в (5.27), которым определяется оптимальный график изменения тока якоря двигателя.

Вопросы и задания

1. Какой является экстремаль в решении задачи оптимального управления ДПТ с моментом сопротивления нагрузки зависящем от угла поворота вала ?

2. С учетом каких условий определяются постоянные интегрирования в рассмотренной задаче оптимального управления ДПТ ?

5.6. Оптимальное управление асинхронным

двигателем в установившемся режиме

Рассмотрим задачу частотного управления АД по критерию минимума тепловых потерь в обмотках статора и ротора.

Используем простейшую Г-образную схему замещения АД (рис.5.8). На статор подается напряжение сети величиной U и частотой ω. К валу двигателя приложен момент сопротивления М нагрузки постоянной величины. Нагрузка имеет момент инерции J. Режим работы установившийся с ω_∂=const или s=const.

В первом приближении можно считать приложенное напряжение U равным э.д.с. Е статора:

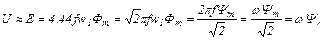(5.31)

где Ψ_m - амплитуда потокосцепления магнитного поля в зазоре АД.

Непосредственно из схемы замещения следует

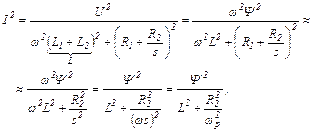
где ω_р - частота тока в роторе.

Обозначим

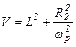
Мощность потерь в обмотках АД

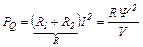
Вращающий момент двигателя

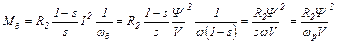
Уравнение динамики электропривода

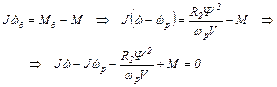
Сформулируем задачу оптимального управления: определить законы изменения сигналов ω, ω_р и Ψ, при которых достигается минимум тепловых потерь в обмотках АД (функционал)

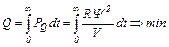
с учетом уравнения связи

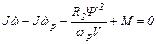
Расширенная функция

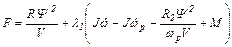
Уравнение Эйлера по переменной ω и его решение:

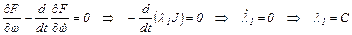
Уравнение Эйлера по переменной Ψ² и его решение:

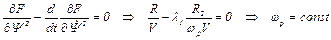
Для установившегося режима работы электропривода выполняется равенство

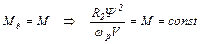(5.32)

Так как ω_p=const, то в соответствии с (5.32) также Ψ=const.

Таким образом, оптимальное управление, при котором тепловые потери в обмотках АД минимальны, достигаются при поддержании постоянства потокосцепления и частоты тока в роторе:

ω_p=const и Ψ=const

При Ψ=const в соответствии с (5.31) отношение напряжения U питания АД к частоте ω этого напряжения является постоянной величиной

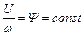
Таким образом, расчеты по простейшей схеме замещения при учете приближенного равенства 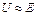показали, что минимум потерь мощности при частотном управлении достигается при пропорциональности U и ω, т.е. при так называемом законе частотного управления Костенко.

Расчеты по полной Т-образной схеме замещения и отказ от приближенного равенства 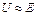выполняются в целом также, но с большими сложностями вычислительного характера.

Вопросы и задания

1. Как рассчитать ток статора АД по схеме его замещения ?

2. Как рассчитать вращающий момента АД и составить уравнение движения электропривода с АД ?

3. Сформулируйте постановку задачи оптимального управления АД в установившемся режиме.

4. Как нужно оптимально изменять величину и частоту питающего АД напряжения в установившемся режиме его работы ?

5.7. Оптимальное по минимуму расхода топлива

управление движением судна

Параметрами движения судна в рейсе являются пройденное расстояние s и v скорость движения в текущий момент времени (рис.5.9).

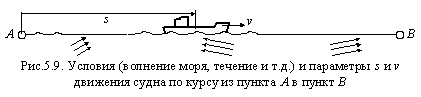
Если g=g(s,v) – секундный расход топлива (кг/сек), зависящий от пройденного судном пути s и его скорости v ( 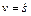), то массовый расход топлива за время Т рейса будет равен

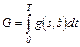, кг (5.33)

Минимум расхода топлива будет достигнут, если регулирование его расхода g производить в зависимости от s и v так, чтобы выполнялось уравнение Эйлера для функционала (5.33)

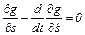(5.34)

Решением уравнения Эйлера, в котором подинтегральная функция не зависит явно от времени t, является

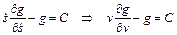, (5.35)

где С – постоянная величина для всего рейса.

Для доказательства этого сначала преобразуем уравнение (5.34), освободившись в нем от символа повторной производной:

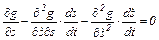, (5.36)

а затем возьмем производную от решения (5.35)

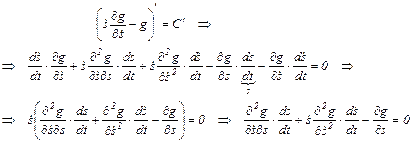(5.37)

Последнее выражение цепи (5.37) совпадает с (5.36), что и требовалось доказать.

Постоянная С определяется на основании расходных характеристик, зависящих от глубины фарватера, загрузки судна, бальности волнения моря, скорости и направления ветра и др. Для судов расходные характеристики имеют вид, приведенный на рис.5.10. Эти характеристики перестраиваются в характеристики, приведенные на рис.5.11. В выбранной точке 0 определяются значения g₀, v₀ и 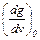, затем вычисляется выражение 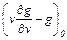и при заданном значении v₀ образуется одна точка на графике рис.5.11.

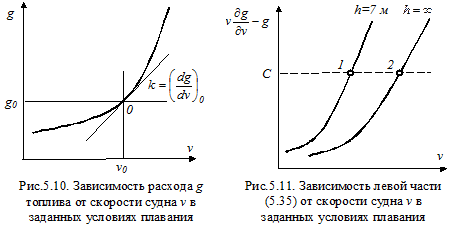
По графикам, приведенным на рис.5.11, можно обосновать стратегию оптимального управления. Она заключается в том, что на участках движения, где велико сопротивление движению (точка 1) скорость нужно уменьшить, но зато на участках с малым сопротивлением движению (точка 2) скорость должна быть выше средней скорости за рейс. Именно так и ездят автомобилисты: на спусках скорость увеличивают, а на подъёмах сбрасывают.

Структурная схема оптимальной по расходу топлива САУ, регулятор которой работает в соответствии с выражением (5.35), приведена на рис.5.12.

Арифметический блок вычисляет приближенное значение выражения (5.35), подключаясь периодически к сигналам g и v. Из текущих g_n и v_n и хранящихся в памяти арифметического блока предшествующих их значений g_n-1 и v_n-1 вычисляются сначала сигналы ∆g и ∆v изменений g и v, а затем вычисляется значение 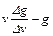. Если оно оказалось меньше постоянной С, то это значит, что скорость меньше оптимальной и следует повышать подачу топлива до тех пор, пока сигнал ε обратится в ноль.

Синтезированная оптимальная САУ является поисковой периодического действия. Оптимальный режим движения обеспечивается без наличия детальной информации о зависимости интенсивности расхода топлива g от параметров движения.

Вопросы и задания

1. От каких факторов движения судна зависит полный расход топлива ?

2. Как нужно оптимально изменять величину секундного расхода топлива во время рейса ?

3. Обоснуйте структурную схему оптимальной по массовому расходу топлива САУ движением судна по курсу.

5.8. Методы оптимального управления,

основанные на принципе максимума Понтрягина

Принцип максимума разрабатывался специально для решения задач оптимального управления на фазовые переменные которого наложены ограничения типа неравенств.

Главными достоинствами метода являются:

- достаточно простое определение экстремалей, состоящих из кусочно-непрерывных функций, которые могут иметь разрывы (изменяться скачком);

- учитываются ограничения типа неравенств (5.7).

Теоремы принципа максимума справедливы для систем управления, поведение которых описывается системой дифференциальных уравнений первого порядка:

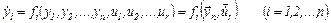(5.38)

где у_i - фазовые координаты объекта; u_j - управления.

Базовая постановка задачи оптимального формулируется следующим образом: отыскать управления и u(t), переводящие систему за время Т из положения у(0) в положение у(Т) и доставляющие экстремум функционалу

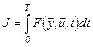(5.39)

Решение, полученное в такой постановке, затем распространяется (трансформируется) на оптимальные САУ произвольного типа.

Переход к описанию объекта управления в виде системы уравнений вида (5.38) от линейного уравнения n-го порядка, например, осуществляется путем замены переменных 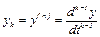и подстановки их в исходное уравнение. Пусть уравнение объекта с одним управляющим воздействием и имеет вид

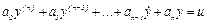
Тогда, обозначая 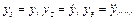можем записать систему п уравнений первого порядка, эквивалентную системе (5.38):

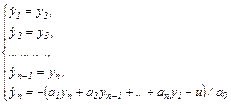
В число фазовых координат объекта включают еще величину у₀, характеризующую текущее значение функционала, т.е.

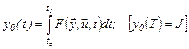
Дифференциальное уравнение для координаты у₀ записывается

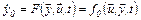(5.40)

Добавляя уравнение (5.40) в (55.1), запишем окончательно систему уравнений задачи оптимального управления:

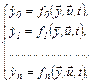или в общем виде 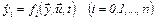(5.41)