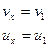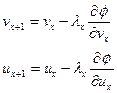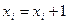Оделирование рабочего процесса на основании баланса мощности и производительности.

Балланс производительности:

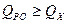, где

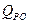- производительность по рабочему органу;

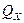- производительность по ходу.

Производительность по рабочему органу зависит от его конструкции и принципа работы. Для большинства машин экскавирующих материал, производительность по ходу можно найти по формуле:

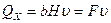, где

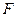- площадь сечения экскавирующего слоя перпендикулярно направлению скорости машины;

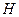- глубина экскавации;

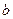- ширина захвата;

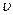- скорость машины по ходу.

Для такого рабочего органа, как цепной бар, производительность находим по формуле:

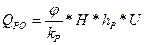, где

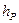– высота профиля;

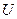– скорость рабочего органа;

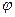– коэффициент заполнения рабочего пространства;

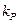– коэффициент разрыхления;

Баланс мощности.

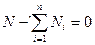, где

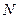– подводимая мощность;

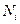– мощность, затрачиваемая на работу агрегата;

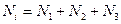, где

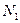– мощность на резание;

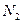–мощность на перемещение материала;

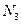– мощность на движение.

Распишем эти три составляющие подводимой мощности:

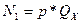, где

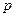– удельная затрачиваемая мощность на резание,

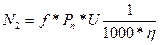, где

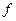–коэффициент трения;

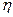– КПД привода бара;

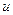– относительная скорость цепи.

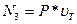, где

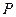– суммарная сила сопротивления движению;

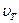– теоретическая скорость движения,

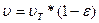, где

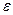– коэффициент буксования,

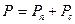, где

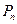– сопротивление подачи рабочего органа;

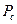– сопротивление движения агрегата,

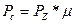, где

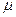– коэффициент сопротивления движению;

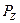– нагрузка со стороны агрегата на опорное основание;

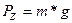, где

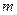– масса агрегата,

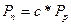, где

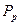– сила сопротивления резанию.

.

,

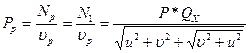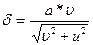где 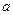– шаг резцов.

Преобразовав, все данные мы получим

;

;

.

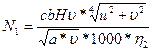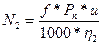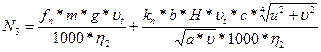Для метода скорейшего спуска необходимо найти частные производные по 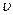и 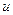для уравнений баланса мощности и баланса производительности.

Итак, принимаем:

;

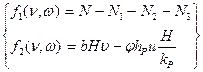Тогда частные производные будут иметь вид:

;

;

;

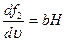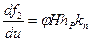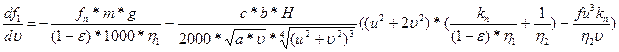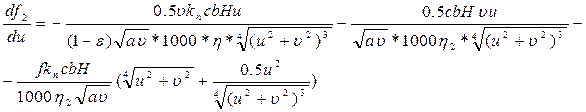
лок-схема алгоритма

	Ввод исходных данных(b,H,m, )
	Ввод приближенных значений

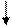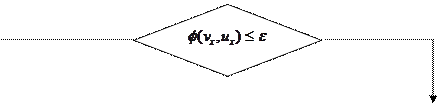Нет Да

лгоритм выполнения программы

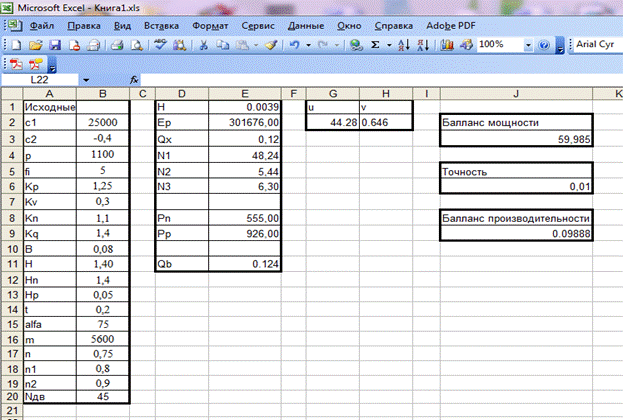
Программа решения уравнений реализована с помощью средств MS Excel

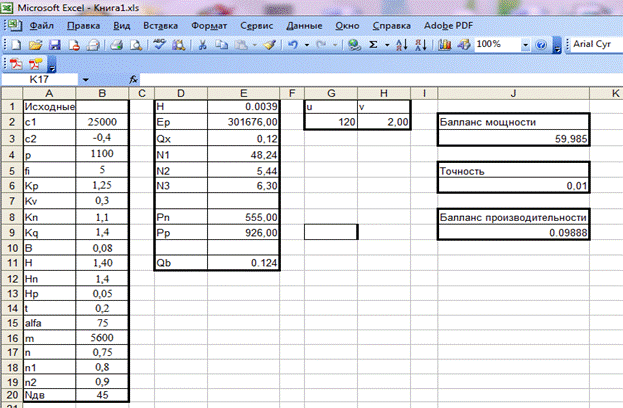
В текущем окне в ячейках A1-A20 пользователь вводит исходные данные к заданию на курсовую работу. Ячейки G2 и H2 содержат первое приближение к решению систему уравнений модели рабочего процесса. Сама система записана в ячейках J3,J9.

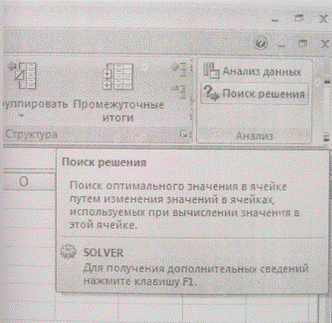
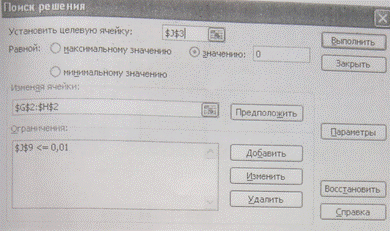
Во вкладке «Параметры» мы указываем точность решения и допустимое значение отклонения и предельное число итераций нашего метода.

Работа программы

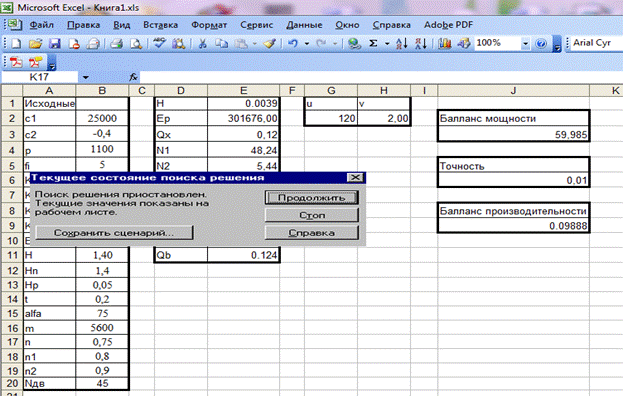
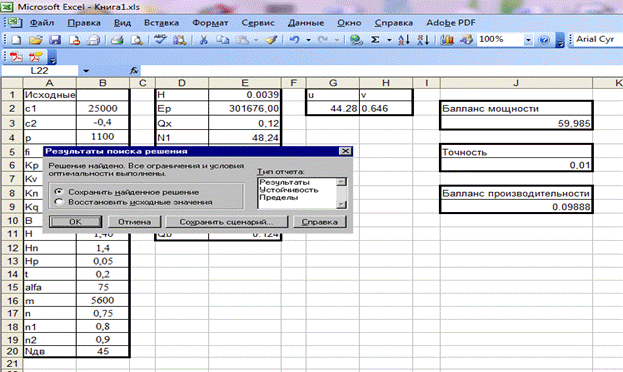
После нахождения корней программа сообщит об этом в отдельном окне.

аключение

В данной курсовой работе мною с помощью метода скорейшего спуска были найдены оптимальные скорости (скорость рабочего органа 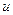и линейная скорость движения машины МГД–6Н)

Была составлена математическая модель работы исполнительного органа. Разработан алгоритм исследования математической модели, написана программа, реализующая этот алгоритм на ПК.

Произведён анализ результатов вычислений. Метод скорейшего спуска является одним из наиболее простых и целесообразных в математическом моделировании и инженерной практике.

Список литературы

1. Замой С.С., Якубойлик О.Э. Программное обеспечение технологии геоинформационных систем. Красноярск: издательство СОРАН, 1998–110с.

2. Доронин С.В. Проектирование и конструирование горных машин и оборудования.

Метод указания к практическим занятиям – Красноярск: ГауМиЗ, 1998–32с.

3. С.В. Скоробогатов, В.В. куколь. Горнопроходческие и строительные машины – Москва: издательство “Недра”, 1985–261с.

4. Конспект лекций по дисциплине “Моделирование и численный анализ”,

Казаченко Г.В., Минск 2003
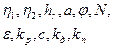