Отримання синусоїдного струму та миттєві значення електричних величин.
Розглянемо найпростіше електричне коло (рис. 2.3, а), яке містить джерело електрорушійної сили Е, з внутрішнім опором r0 та споживач електричної енергії, опір якого r1.
З рівняння закону Ома для цього кола –
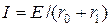 ,
,
випливає, що при незмінних значеннях r0і r1 характер зміни сили струму кола визначається характером зміни ЕРС джерела. Отже, для отримання у колі синусоїдного струму потрібно мати джерело синусоїдної ЕРС.
З курсу фізики відомо, що при змінному у часі перетині витків котушки силовими лініями поля постійного магніту, в витках виникає ЕРС. Аналогічний ефект має місце і при обертанні в однорідному магнітному полі металевої рамки (рис. 2.3, б) діаметром d з постійною швидкістю:
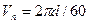 .
.
При цьому активні ділянки (а та b) рамки, кожна з яких має довжину l, перетинають силові лінії магнітного поля і згідно з законом електромагнітної індукції, в них генеруються ЕРС: еа = еb = BlVn. Оскільки положення рамки в будь-який момент часу можна визначити величиною кута a між площиною рамки і геометричною нейтраллю (ГН) системи, то відповідне значення ЕРС буде:
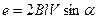 ,
,
де В – магнітна індукція однорідного поля.

 Оскільки в даному випадку B, l і V –сталі величини, то з наведеного рівняння випливає, що, ЕРС рамки є функцією кута a (рис. 2.3, в). Отже,при a = 0 e0 = 0, а коли a = ± p/2–ЕРС сягає максимального (амплітудного) значення:
Оскільки в даному випадку B, l і V –сталі величини, то з наведеного рівняння випливає, що, ЕРС рамки є функцією кута a (рис. 2.3, в). Отже,при a = 0 e0 = 0, а коли a = ± p/2–ЕРС сягає максимального (амплітудного) значення:
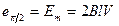 .
.
Це дає підстави записати рівняння ЕРС рамки у вигляді:
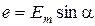
Оскільки кут повороту рамки a = wt, де w = 2pf - кутова швидкість, рад/с; t – час, с, то рівняння розрахунку значень ЕРС в будь-які моменти часу має вид:
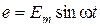
Чисельні значення, які приймає змінна величина в окремі моменти часу називають миттєвими значеннями цієї величини. Миттєві значення електричних величин вимірюють за допомогою осцилографа.
Якщо вважати, що за нескінченно малий проміжок часу Dt змінна величина а, отже, її миттєве значення, практично не змінюються і залишаються сталими, то до миттєвих значень електричних величин змінного струму можна застосовувати всі відомі закони постійного струму.
Таким чином, при використанні розглянутої моделі генератора змінного струму (рис. 2.3, б) в якості джерела ЕРС, струм у колі, яке розглядається (рис. 2.3, а) буде:
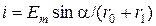 ,
,
а, оскільки амплітудному значенню ЕРС відповідає амплітудне значення струму Im = Em/(r0+r1), то одержимо:
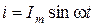 .
.
Враховуючи, що опір зовнішньої ділянки кола становить r1, спад напруги на споживачі буде –
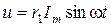
або ж (оскільки Um = r1Im):
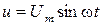 .
.
Для одержання синусоїдного струму у промисловості використовують синхронні генератори, будова і принцип дії яких будуть розглянуті нижче (у розділі “Електричні машини”).
