Интерполяция функций многочленами
Задание.
По заданным точкам составить интерполяционный многочлен Лагранжа и преобразовать его в форму простого полинома.
Выполнить расчет промежуточных точек по полученной формуле с шагом (b-a)/25,
где а и b – крайние точки интервала.
Построить в Mathcad графики:
Заданной табличной функции (большие маркеры без линий);
Ломаной, соответствующей многочлену Лагранжа в вычисленных точках;
Плавной кривой полинома Лагранжа (строится на интервале по аналитической формуле без конкретных точек).
1.
| х | 0,99 | 3,69 | 4,13 | 6,07 | 7,35 |
| у | 22,48 | 26,25 | 44,67 | 8,83 | 56,18 |
2.
| х | -5 | -3 | ||||
| у | -4 | -3 | -2 |
3.
| х | ||||||
| у | 7,79 | 6,06 | 3,84 | 3,04 | 0,67 | 3,59 |
4.
| х | 6,22 | 7,71 | 9,05 | 18,59 | 22,21 |
| у | 14,79 | 8,18 | 17,49 | 21,89 | 23,28 |
5.
| х | -100,00 | -83,42 | -80,51 | -74,01 | -72,27 |
| у | 98,68 | 148,68 | 180,23 | 59,63 | 68,72 |
6.
| х | 1,00 | 18,16 | 46,51 | 47,09 | 74,98 |
| у | 28,02 | 216,87 | 196,49 | 198,92 | 180,22 |
7.
| х | -1,00 | -0,53 | 0,39 | 0,86 | 1,86 |
| у | 28,02 | 216,87 | 405,72 | 594,57 | 783,43 |
8.
| х | -5,00 | -2,80 | -1,09 | -0,23 | 0,30 |
| у | 20,00 | 15,00 | 18,00 | 15,67 | 14,67 |
9.
| х | 2,29 | 3,05 | 5,70 | 6,67 | 7,66 |
| у | 3,27 | 8,52 | 12,07 | 31,04 | 20,47 |
10.
| х | 4,70 | 5,00 | 7,08 | 8,91 | 10,87 |
| у | -2,22 | -5,31 | -22,93 | -1,01 | -75,57 |
11.
| х | 8,20 | 14,90 | 20,40 | 53,10 | 53,29 |
| у | 3,10 | 0,00 | -2,30 | 6,90 | 14,70 |
12.
| х | 34,00 | 43,00 | 49,00 | 59,00 | 68,00 | 74,00 |
| у | 0,14 | 0,11 | 0,10 | 0,08 | 0,07 | 0,07 |
13.
| х | 1,00 | 5,00 | 11,00 | 16,00 | 21,00 | 27,00 |
| у | 6,59 | 1,68 | 14,51 | 16,59 | 11,61 | 37,62 |
14.
| х | 14,00 | 21,00 | 30,00 | 40,00 | 50,00 | 55,00 |
| у | 1,37 | 5,35 | 4,70 | 4,97 | 6,93 | 5,26 |
15.
| х | 0,10 | 1,05 | 1,55 | 2,43 | 2,81 |
| у | 0,31 | 22,84 | 12,66 | 30,30 | 25,07 |
16.
| х | ||||||
| у | 1,39 | 2,24 | 5,28 | 7,22 | 13,98 | 19,73 |
17.
| х | |||||
| у | 1,39 | 3,90 | 10,00 | 84,45 | 597,94 |
18.
| х | ||||||
| у | 1,20 | 1,65 | 2,51 | 2,96 | 3,08 | 3,12 |
19.
| х | -4 | -2 | ||||
| у | 3,00 | 0,00 | -1,00 | 2,00 | 9,00 | 22,00 |
20.
| х | -3 | -1 | ||||
| у | 5,00 | 3,00 | 0,00 | -1,00 | 2,00 | 6,00 |
Пример выполнения
Выполним решение для варианта №8.
Расчеты проведем в среде Mathcad.
Составим интерполяционный полином Лагранжа.
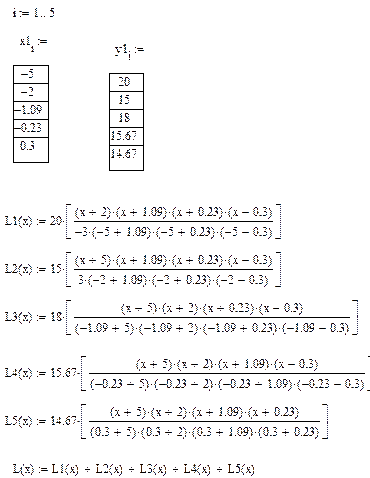
Выполним расчет промежуточных точек по полученной формуле с шагом 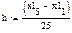 .
.

Построим графики.
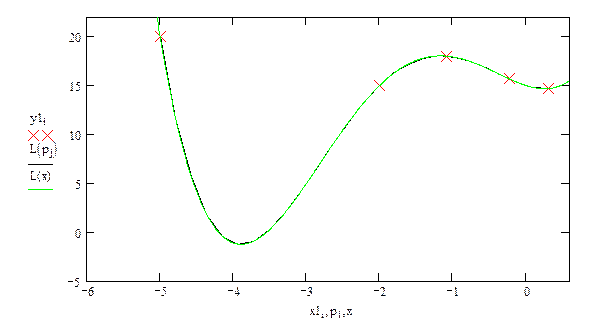
Содержание отчета:
1. Графики функций и полиномов.
2. Выводы.
Контрольные вопросы:
1. Поясните термины: “интерполяция”, “экстраполяция”, “аппроксимация”.
2. Способы приближения функций.
3. Составить интерполяционный многочлен Лагранжа для 2-3 точек.
4. Составить интерполяционный многочлен Ньютона для равноотстоящих узлов.
5. Составить интерполяционный многочлен Ньютона для неравноотстоящих узлов.
6. Формулы кусочно-квадратичной интерполяции.
Лабораторная работа №4
Аппроксимация функций методом наименьших квадратов
1 Методом наименьших квадратов подобрать коэффициенты аппроксимирующей функции (по вариантам) и построить график аппроксимации с исходными точками.
2 Составить программу для выполнения задания, а также выполнить его в пакете Mathcad. Построить графики табличной функции (маркерами) и аппроксимирующей.
3 Найти все отклонения и среднеквадратическое отклонение аппроксимирующей функции от заданной табличной, заполнив таблицу:
| xi | x1 | x2 | ... | xn |
| yi | y2 | y2 | ... | yn |
| Ф(xi) | Ф(x1) | Ф(x2) | ... | Ф(xn) |
| Dyi | ... |
Среднеквадратическое отклонение:
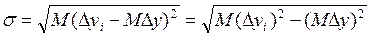
М – математическое ожидание (среднее арифметическое)
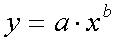 |  | |
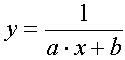 |  | |
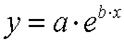 |  | |
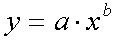 |  | |
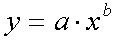 |  | |
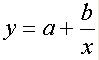 |  | |
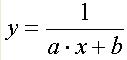 | 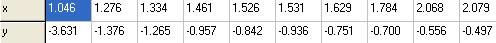 | |
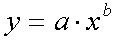 |  | |
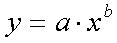 |  | |
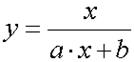 |  | |
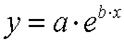 |  | |
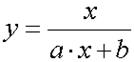 |  |
Содержание отчета:
1. Вывод и решение системы для определения коэффициентов полинома.
2. Таблицы.
3. Графики функций и полиномов.
4. Выводы.
Контрольные вопросы:
1. Сравните полиномиальную интерполяцию табличной функции многочленами и аппроксимацию по методу МНК.
2. Какие функции обычно выбираются в качестве аппроксимирующих (приведите формулы).
3. Способы линеаризации зависимостей.
4. В чем заключается основная идея МНК?
Лабораторная работа №5
