A. квадратичная функция (эллипс)

Курсовой проект

“Моделирование процесса параметрической идентификации динамического объекта”

По дисциплине: математические модели

Вариант №7.

Выполнил:

студент группы 23504/21

Груздев К. С.

Преподаватель:

Леонтьева Т. В.

Санкт-Петербург

2013 год

Исходные данные: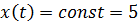

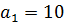
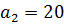
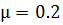
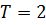
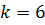
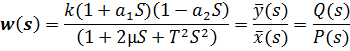
Часть 1. Преобразование формулы и решение ее с помощью Метода Эйлера

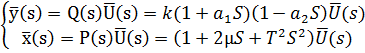
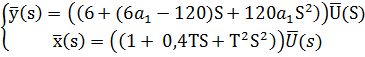
Перейдём в вещественную форму:

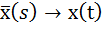
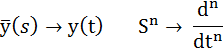
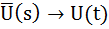
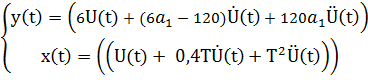
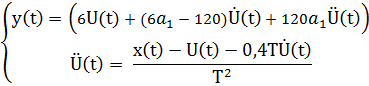
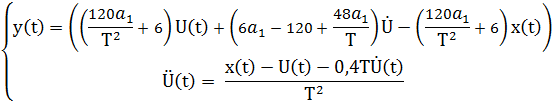
Обозначим:

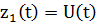
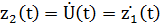
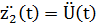
Получим систему уравнений в канонической форме:

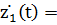
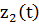
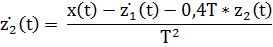
Далее решаем систему методом Эйлера

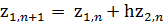
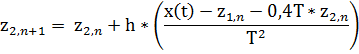
А также, на каждом шаге подставив полученные значения, рассчитываем

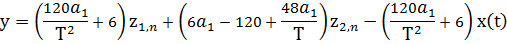
Выберем шаг h=0.5, выполним необходимые вычисления и построим график функции.

Полученный график представлен на рис.1. По графику видно, что функция

y(t)-> к числу чуть больше 0. А выходит она из точки ~ -1500.
Узнаем точные значения этих точек. Для этого вычислим пределы:

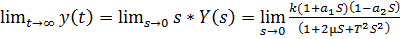= 30

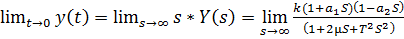= -1500

Некоторые значения y представлена в таблице 1 “ Зависимость значения функции от времени”.

Наилучший период наблюдения t=1...300, шаг h=0.5.

Взято 300 точек, т.к. уже на этом периоде наблюдения видно как график функции сходится к положительному числу около 0. График функции искажается при шаге больше 0.5 (при шаге больше 0,8 - расходится). А при меньшем шаге сходимость получим за большее число шагов. Поэтому выбран шаг h=0.5.

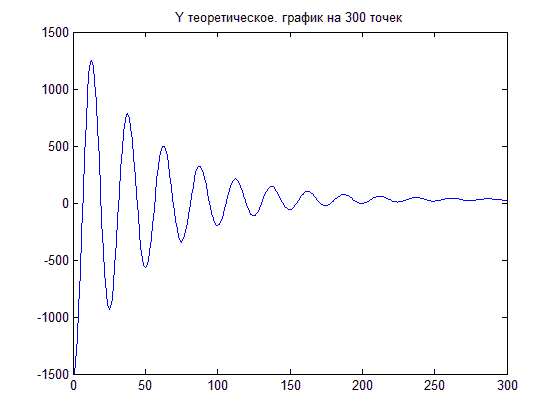
(рис.1)

Таблица 1

“Зависимость значения функции от времени”

t	y(t)
	-1500
	1130,33569982263
	-407,472269924090
	-131,811172218857
	546,368398013440
	-554,815355895296
	465,038634809155
	-156,677691301819
	-15,5099285734393
	218,653161918972
	-192,944828877209
	201,440561416127
	-48,6973993327229
	18,9739612829796
	98,5444137678508
	-54,7630972652742
	97,3519023534570
	-2,84302221765938
	28,2615453956948
	54,7510635292838
	-2,13806225774806
	56,3810973500383
	16,4104765802804
	30,2954912892119
	38,8749721864901
	17,8493005972232
	40,3035993332771
	24,4184897222613
	30,4841608516322
	33,1566814566145

Часть 2. Моделирование метода оптимизации.

МЕТОД ПОКООРДИНАТНОГО СПУСКА

Описание метода поиска

Метод предназначен для нахождения экстремума (минимума) функции ,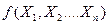

но в нашем случае: .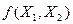

1. Задается начальная точка 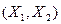, отличная от точки минимума. Задаются точность (E) и шаг (h).

2. Далее выбираем координату (направление), по которой будем двигаться по функции:

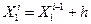
а все остальные координаты фиксируем. И ищем минимальное значение функции как функцию одной переменной (Х₁)

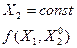
В случае если новое значение функции больше предыдущего, то меняем шаг на противоположный (h = -h).

3. Когда находим значение координаты, при котором значение функции минимально, то выбираем другую координату, по которой будем двигаться по функции:

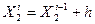
а все остальные координаты снова фиксируем.

Выбор остановки задан 4 условиями:

1.

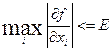
2.

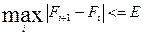
3.

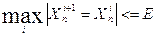
4. Число обращений (итераций)

k_(f) > k_max

В данном случае я использовал 2 и 4 условия, т. к. 3 условие не подходит из-за того, что шаг постоянный, а 1 условие – затрачивает больше ресурсов.

2) Результаты работы программы:

a. Квадратичная функция (Эллипс)

Функция имеет вид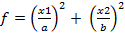

i. Начальная точка А0 (2, 2).

EPSILON = 0.001; %Точность

h = 0.2; %Шаг

a = 3;

b = 2;

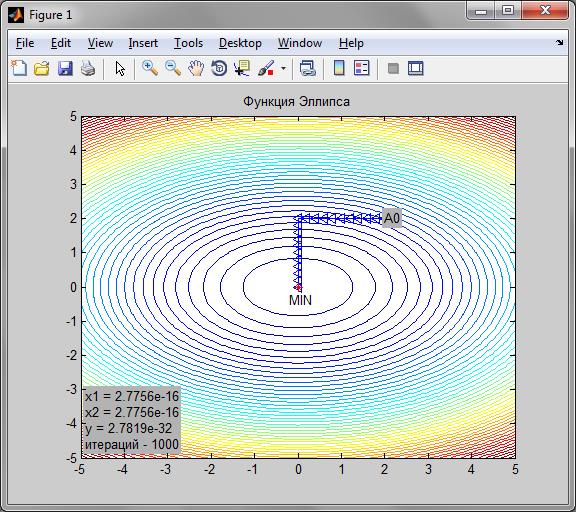
(рис.2)

№ шага	X1	X2
	1,8
	1,6
	1,4
	1,2
	0,8
	0,6
	0,4
	0,2
	2,78E-16
	2,78E-16	1,8
	2,78E-16	1,6
	2,78E-16	1,4
	2,78E-16	1,2
	2,78E-16
	2,78E-16	0,8
	2,78E-16	0,6
	2,78E-16	0,4
	2,78E-16	0,2
	2,78E-16	2,78E-16

N = 21

ii.

b. функция Розенброка

Функция имеет вид:

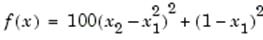
i. Начальная точка А0 (2, 2).

EPSILON = 0.001; %Точность

h = 0.1; %Шаг

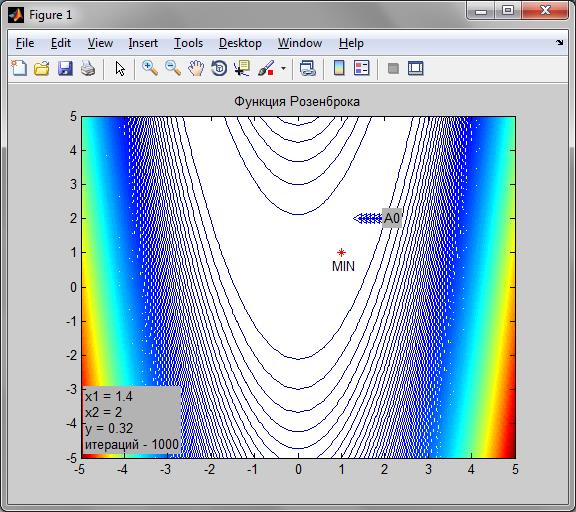
(рис.3)

№ шага	X1	X2
	1,9000
	1,8000
	1,7000
	1,6000
	1,5000
	1,4000

N = 7

ii. Начальная точка А0 (1, -4).

EPSILON = 0.001; %Точность

h = 0.1; %Шаг

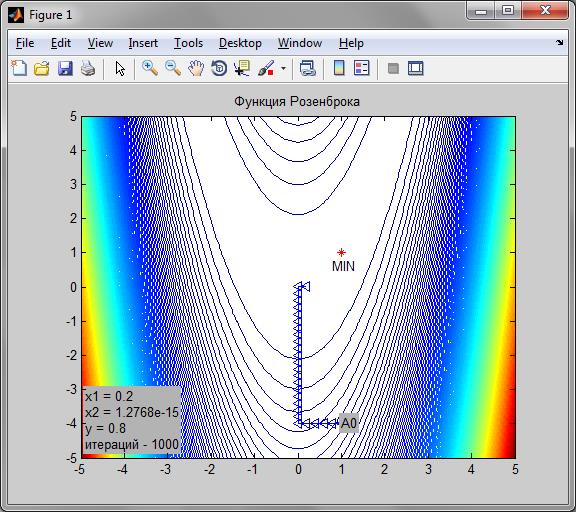
(рис.4)

№ шага	X1	X2
		-4
	0,8	-4
	0,6	-4
	0,4	-4
	0,2	-4
	5,55E-17	-4
	5,55E-17	-3,8
	5,55E-17	-3,6
	5,55E-17	-3,4
	5,55E-17	-3,2
	5,55E-17	-3
	5,55E-17	-2,8
	5,55E-17	-2,6
	5,55E-17	-2,4
	5,55E-17	-2,2
	5,55E-17	-2
	5,55E-17	-1,8
	5,55E-17	-1,6
	5,55E-17	-1,4
	5,55E-17	-1,2
	5,55E-17	-1
	5,55E-17	-0,8
	5,55E-17	-0,6
	5,55E-17	-0,4
	5,55E-17	-0,2
	5,55E-17	1,28E-15
	0,2	1,28E-15

N = 27

Блок-схема основной программы: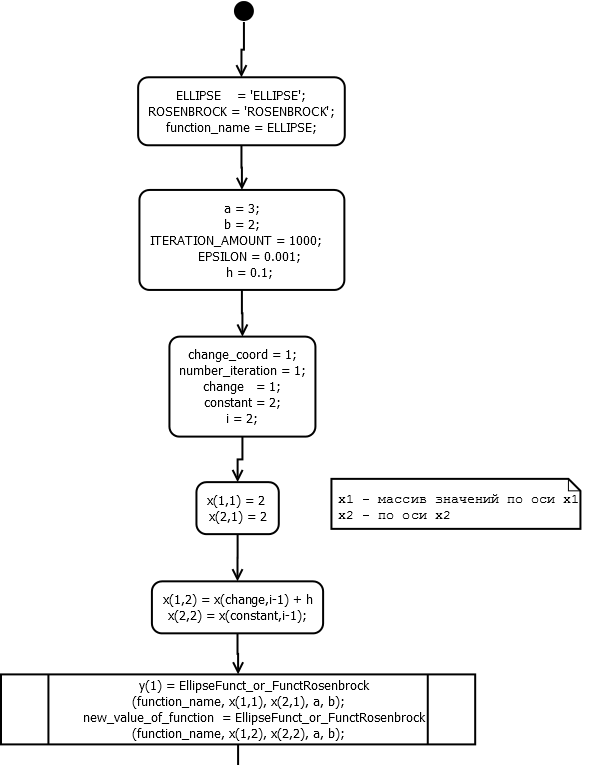

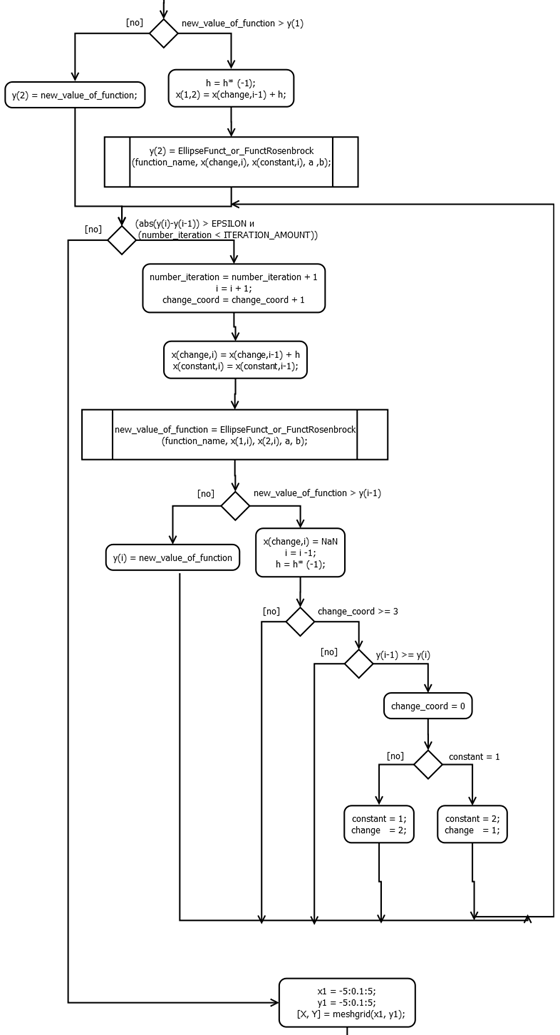
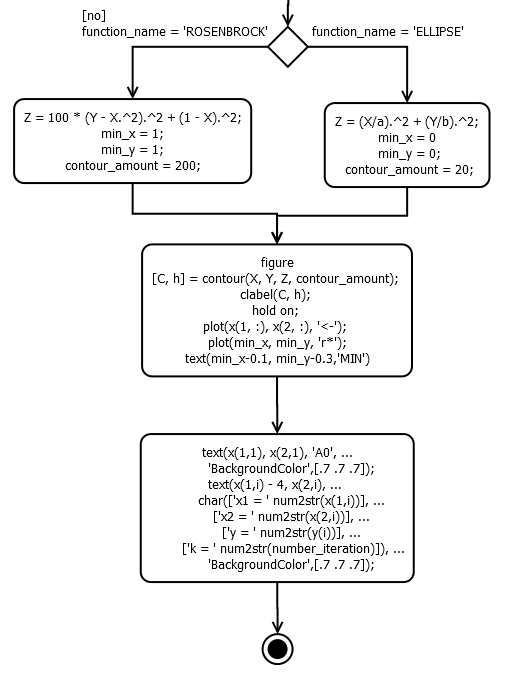
Блок-схема функции

y = EllipseFunct_or_FunctRosenbrock(function_name, x_0_i, x_1_i, a, b):

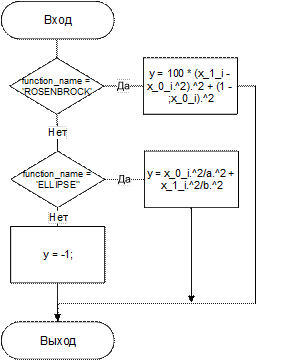
Выводы ко второй части:

Ввиду того, что метод покоординатного спуска нулевого порядка, он довольно неточен. Из-за того, что функция розенброка имеет овражный рельеф, дойти до точки минимума не удалось, из-за. Точка остановки в этом случае была довольно далеко от точки минимума. В случае с функцией Эллипса точка минимума была достигнута за 21 итерацию, при шаге h = 0.2

Часть 3. Шум.

Создание ГСЧ и поиск модели зашумленного сигнала.

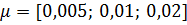, т. к. y_max по модулю равен 1500 (> 500).

Проверка генератора «Треугольного шума» при N = 10000 и delta_y = 7.5:

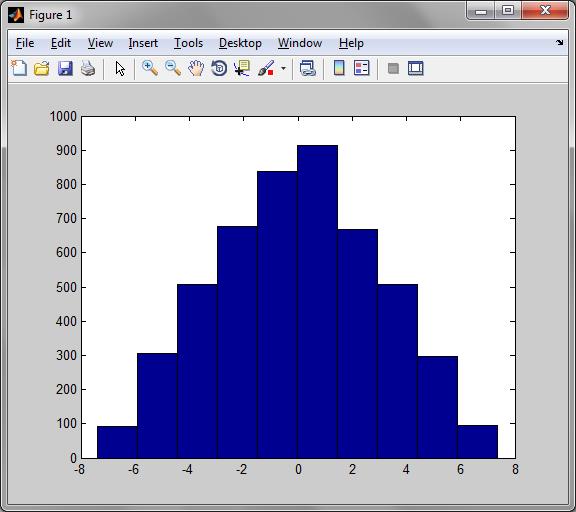
(рис.5)

График Y теоретического и Y экспериментального (зашумленный график Y теоретического)

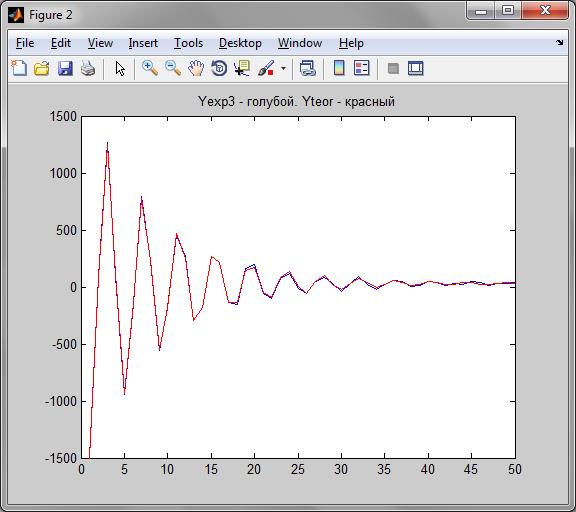
(рис.6)

Таблица 2

«Значения Yэкс в зависимости от 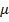шума»