Перечень тем лабораторных работ
Согласно учебному плану выполнение лабораторных работ по данной дисциплине не предусмотрено.
Вопросы для контроля и самоконтроля
Семестр
1. Алгебраическая форма комплексного числа.
2. Действия над комплексными числами, записанными в алгебраической форме.
3. Тригонометрическая форма комплексного числа. Модуль и аргумент комплексного числа.
4. Действия над комплексными числами, записанными в тригонометрической форме.
5. Формула Муавра.
6. Формула извлечения корня n-й степени из комплексного числа.
7. Корни n-й степени из единицы.
8. Понятие инверсии и понятие транспозиции в перестановке.
9. Четные и нечетные перестановки.
10. Способы вычисления определителей 2-ого и 3-его порядков.
11. Определение детерминанта (определителя) порядка n.
12. Свойства определителей.
13. Определение минора и алгебраического дополнения.
14. Формула разложения определителя по строке, по столбцу.
15. Определение решения системы линейных уравнений.
16. Определение равносильных систем уравнений.
17. Эквивалентные преобразования систем линейных уравнений.
18. Возможное число решений системы линейных уравнений.
19. Какие системы можно решить методом Крамера и сколько решений имеют такие системы.
Семестр
1. Действие сложения матриц. Какие матрицы можно складывать?
2. Свойства операции сложения.
3. Действие умножения матрицы на число. Свойства этого умножения.
4. Действие умножения матриц. Какие матрицы можно перемножать?
5. Свойства операции умножения.
6. Определение обратной матрицы. Для каких матриц существует обратная матрица?
7. Формула для вычисления обратной матрицы.
8. Определение векторного пространства.
9. Примеры векторных пространств.
10. Определение линейно зависимой системы векторов.
11. Определение линейно независимой системы векторов.
12. Определение максимальной линейно независимой подсистемы системы векторов.
13. Определение ранга системы векторов.
14. Определение базиса и размерности векторного пространства.
15. Привести примеры базиса и определить размерность векторных пространств 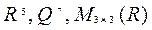
16. Определение строчного ранга матрицы.
17. Определение столбцового ранга матрицы.
18. Определение минорного ранга матрицы.
19. Формулировка теоремы о ранге матрицы.
20. Формулировка Теоремы Кронекера-Капелли.
21. Однородная система линейных уравнений.
22. Сколько решений может иметь однородная система линейных уравнений?
23. Фундаментальная система решений однородной системы.
24. Определение и примеры бинарных алгебраических операций.
25. Определение и примеры унарных алгебраических операций.
26. Определение и примеры группы.
27. Свойства групп.
28. Определение и примеры подгруппы.
29. Критерий подгруппы.
30. Определение и примеры кольца.
31. Свойства колец.
32. Определение и примеры подкольца.
33. Критерий подкольца.
34. Определение и примеры поля.
35. Свойства поля.
36. Определение и примеры подполя.
37. Критерий подполя.
Семестр
1. Определение степени многочлена.
2. Действия над многочленами.
3. Частное и остаток от деления многочлена на многочлен.
4. Определение НОД многочленов.
5. Способ нахождения НОД двух многочленов.
6. Способ нахождения НОД трех многочленов.
7. Взаимно простые многочлены.
8. Свойства взаимно простых многочленов.
9. Определение кратности корня.
10. Основная теорема алгебры многочленов.
11. Следствия из основной теоремы алгебры.
12. Теорема Безу.
13. Схема Горнера.
14. Формулы Виета.
15. Способ нахождения рациональных корней многочленов с целыми коэффициентами.
16. Определение приводимого многочлена.
17. Определение неприводимого многочлена.
18. Свойства неприводимых многочленов.
19. Какие многочлены приводимы и какие многочлены неприводимы над
полем С?
20. Какие многочлены приводимы и какие многочлены неприводимы над
полем R?
21. Необходимое и достаточное условие приводимости многочлена 2-й или 3-ей степени над полем Q.
22. Критерий Эйзенштейна.
23. Привести пример многочлена 6-й степени, приводимого над полем Q и пример многочлена 6-й степени, неприводимого над полем Q.
Семестр
1. Определение и критерий подпространства векторного пространства.
2. Пересечение подпространств.
3. Сумма подпространств.
4. Будет ли объединение подпространств подпространством?
5. Прямая сумма подпространств.
6. Критерий прямой суммы подпространств.
7. Определение изоморфизма векторных пространств.
8. Определение матрицы перехода от одного базиса к другому.
9. Какими свойствами обладает матрицы перехода?
10. Какова связь координат одного и это же вектора в разных базисах?
11. Определение и примеры линейного оператора.
12. Матрица линейного оператора.
13. Образ линейного оператора.
14. Ядро линейного оператора.
15. Связь между матрицами линейного оператора в разных базисах.
16. Определение и примеры собственного вектора линейного оператора.
17. Определение характеристического корня матрицы.
18. Связь между собственными значениями линейного оператора и характеристическими корнями матрицы.
19. Линейный оператор с простым спектром.
20. В каком базисе матрица линейного оператора диагональна?
21. Определение и примеры групп.
22. Определение циклической группы, порожденной элементом «а».
23. Бесконечная циклическая группа.
24. Конечная циклическая группа порядка n.
25. Определение смежного класса по подгруппе.
26. Свойства смежных классов.
27. Теорема Лагранжа.
28. Найти все подгруппы циклической группы порядка 8
29. Определение нормального делителя.
30. Критерий нормального делителя.
31. Строение фактор-группы по нормальному делителю.
