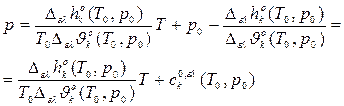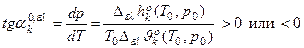Уравнения связей между стандартными мольными характеристиками возгонки
Особенности системы.
1) {k(α)} 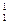 = {1(ε), 1(λ)} = {k(ε), k(λ)},где 1 – номер, k – вид единственного компонента в системе;
= {1(ε), 1(λ)} = {k(ε), k(λ)},где 1 – номер, k – вид единственного компонента в системе;
2) {T, p, { 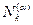 }
} 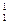 } = {T, p,
} = {T, p, 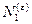 и
и 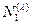 } = {T, p,
} = {T, p, 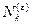 и
и 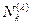 }, где
}, где 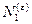 =
= 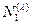 = 1,
= 1, 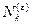 =
= 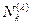 =1;
=1;
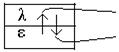 3)
3)
Фазовые переходы  компонента k.
компонента k.
4) Число независимых ЗСФР = К(А-1) = 1(2-1) = 1.
Дифф. форма ЗСФР (дифф. форма уравнения Клаузиуса - Клапейрона).
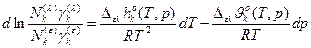
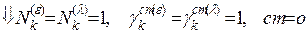
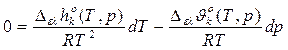
 Т – свободная переменная
Т – свободная переменная
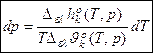 – дифф. форма ЗСФР.
– дифф. форма ЗСФР.
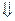 Анализ
Анализ
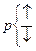 с ↑Т и наоборот, если
с ↑Т и наоборот, если 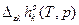 и
и 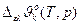 имеют
имеют 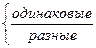 знаки.
знаки.
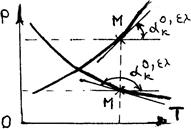
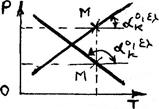
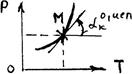
 Граф образ р(Т)
Граф образ р(Т)
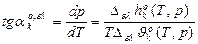
Интегральная форма ЗСФР (интегральная форма уравнения Клаузиуса - Клапейрона).
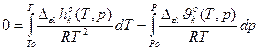 ,
,
|
где
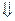 Учёт возможных агрегатных состояний фаз
Учёт возможных агрегатных состояний фаз
| а) ε – конденсир. фаза (ж,т) λ – неконденсир. фаза (п) | б) ε, λ – конденсир. фазы (ж, т) | ||||
Приближения: 1) 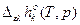 = = 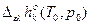 =const, 2) =const, 2) 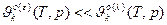 , 3) , 3) 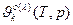 = = 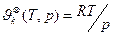 - приближение пар. фазы к чистому ид. газу. - приближение пар. фазы к чистому ид. газу. 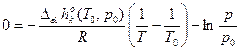 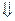 Т – свободная переменная Т – свободная переменная
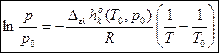 - -
где
экспоненц. вариант интегр. формы ЗСФР, где
| Приближения: 1) 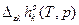 = = 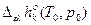 =const, 2) =const, 2) 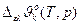 = = 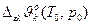 = const. = const.  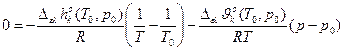
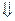 Т – свободная переменная Т – свободная переменная
где
|
Уравнения связей между стандартными мольными характеристиками
фазового перехода ελ в однокомпонентных системах.
1) Общие уравнения связей:
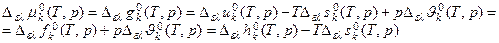
2) Дополнительное уравнение связи из условия равновесия двух фаз ε и λ 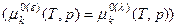 :
:
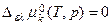
3) Результат совместного рассмотрения 1) и 2) :
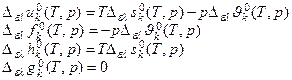

Равновесие жидкость-пар.
Особенности системы.
1) {k(α)} 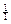 ={1(ж),1(п)}={k(ж),k(п)}, где 1- номер, k- вид единственного компонента;
={1(ж),1(п)}={k(ж),k(п)}, где 1- номер, k- вид единственного компонента;
2) {T,p,{N 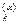 }
} 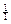 }={T,p,N
}={T,p,N 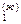 и N
и N 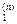 }={ T,p,N
}={ T,p,N 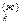 и N
и N 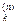 }, где N
}, где N 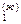 =N
=N 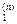 =1, N
=1, N 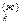 =N
=N 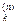 =1;
=1;
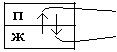
3) 
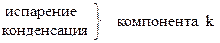
4) Число независимых ЗСФР = К(А-1) = 1(2-1) = 1.
Дифф. форма ЗСФР (дифф. форма уравнения Клаузиуса - Клапейрона).
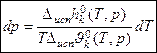 – дифф. форма ЗСФР.
– дифф. форма ЗСФР.
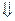 Анализ
Анализ
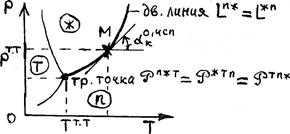
р↑ с ↑Т и наоборот, т.к. 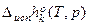 >0 и
>0 и 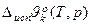 >0.
>0.
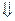 Граф. образ р(Т)
Граф. образ р(Т)
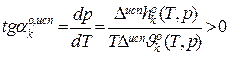
Интегральная форма ЗСФР (интегральная форма уравнения Клаузиуса - Клапейрона).
С учётом приближений 1), 2), 3) в разделе 10.1.3, а) имеем
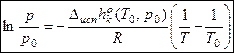 – логарифм. вариант интегр. формы ЗСФР.
– логарифм. вариант интегр. формы ЗСФР.
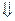 Линеаризация
Линеаризация
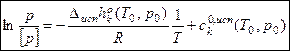 , где
, где 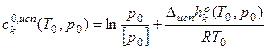 –
–
y = a * x + b – постоянная испарения.
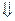 Граф образ
Граф образ 
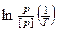
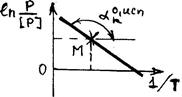
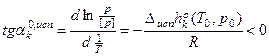
 Освобождение от ln
Освобождение от ln
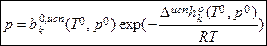 , где
, где 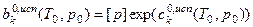
-экспоненц. вариант интегр. формы ЗСФР -предэкспонент при испарении
 Граф. образ р(Т)
Граф. образ р(Т)
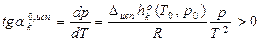
Уравнения связей между стандартными мольными характеристиками испарения.
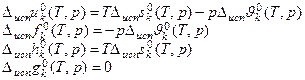
9.3. Равновесие твердь – пар.
Особенности системы.
1) {k(α)} 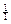 ={1(т),1(п)}={k(т),k(п)}, где 1- номер, k- вид единственного компонента;
={1(т),1(п)}={k(т),k(п)}, где 1- номер, k- вид единственного компонента;
2) {T,p,{N 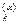 }
} 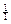 }={T,p,N
}={T,p,N 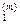 и N
и N 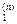 }={ T,p,N
}={ T,p,N 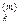 и N
и N 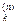 }, где N
}, где N 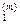 =N
=N 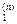 =1, N
=1, N 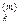 =N
=N 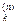 =1;
=1;
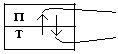
3) 
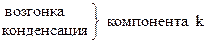
4) Число независимых ЗСФР = К(А-1) = 1(2-1) = 1.
Дифф. форма ЗСФР (дифф. форма уравнения Клаузиуса-Клапейрона).
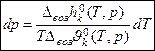 – дифф. форма ЗСФР.
– дифф. форма ЗСФР.
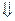 Анализ
Анализ
р↑ с ↑Т и наоборот, т.к. 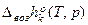 >0 и
>0 и 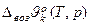 >0.
>0.
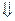 Граф. образ р(Т)
Граф. образ р(Т)
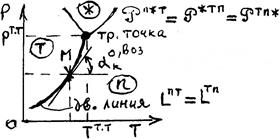
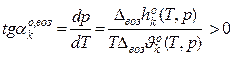
Интегральная форма ЗСФР (интегральная форма уравнения Клаузиуса-Клапейрона).
С учётом приближений 1), 2), 3) в разделе 9.1.3, а) имеем
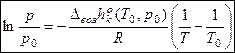 – логарифм. вариант интегр. формы ЗСФР.
– логарифм. вариант интегр. формы ЗСФР.
 Линеаризация
Линеаризация
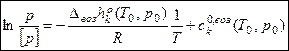 , где
, где 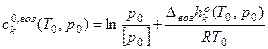 –
–
y = a * x + b – постоянная возгонки.
 Граф образ
Граф образ 
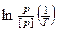
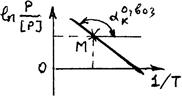
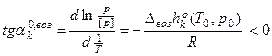
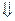 Освобождение от ln
Освобождение от ln
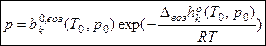 , где
, где 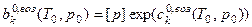
-экспоненц. вариант интегр. формы ЗСФР -предэкспонент при испарении
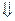 Граф. образ р(T)
Граф. образ р(T)

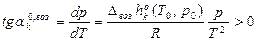
Уравнения связей между стандартными мольными характеристиками возгонки.
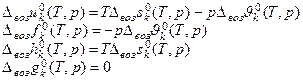
9.4. Равновесие твердь – жидкость.
Особенности системы.
1) {k(α)} 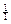 ={1(т),1(ж)}={k(т),k(ж)}, где 1- номер, k- вид единственного компонента;
={1(т),1(ж)}={k(т),k(ж)}, где 1- номер, k- вид единственного компонента;
2) {T,p,{N 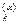 }
} 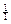 }={T,p, N
}={T,p, N 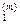 и N
и N 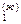 }={ T,p, N
}={ T,p, N 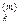 и N
и N 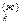 }, где N
}, где N 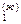 =N
=N 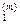 =1, N
=1, N 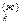 =N
=N 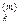 =1;
=1;
3)
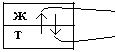
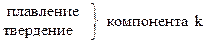
4) Число независимых ЗСФР = К(А-1) = 1(2-1) = 1.

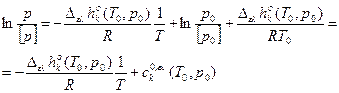
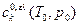 - постоянная фаз. перехода ελ.
- постоянная фаз. перехода ελ.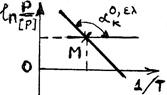
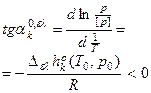
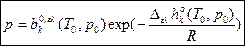
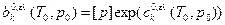 - предэкспонент при фазовом переходе ελ
- предэкспонент при фазовом переходе ελ
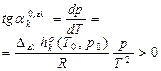
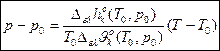 –
–