Некоторые свойства алгоритм золотого сечения.

Утверждение 1. Точки расположены симметрично относительно концов текущего интервала неопределенности.

Действительно, из (3) следует, что точка отстоит от точки на величину ; точка отстоит от точки на ту же величину

Утверждение 2. Для любого 1 алгоритм золотого сечения обладает следующим свойством: одна из точек , совпадает с одной из точек , .

Доказательство. Пусть на 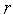-й итерации 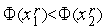. В соответствии с алгоритмом золотого сечения причем, очевидно, ТИН_r+1 . Для того, чтобы доказать справедливость утверждения достаточно показать, что верно отношение

(4)

Из соотношений (3) следует, что

.

Аналогично имеем

Разделив первый из этих результатов на второй, получим

(5)

Из уравнения (2) следует, что 1- = . Отсюда и из (5) следует справедливость (4).

Аналогично проводится доказательство для случая

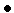
Указанное свойство алгоритма золотого сечения позволяет на каждой итерации (кроме первой) производить испытания только в одной точке.

Из схемы алгоритма золотого сечения имеем.

Утверждение 3. В результате одной итерации алгоритма золотого сечения длина текущего интервала неопределенности сокращается в раз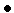

Поэтому количество итераций 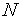, необходимых для нахождения минимума функции с точностью 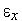, находится из условия

Метод Фибоначчи

Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции 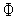( 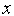), определенной в замкнутой области допустимых значений =[ , ],

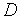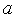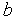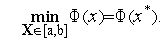
Числа Фибоначчи и их некоторые свойства.

Числа Фибоначчи задаются следующим рекуррентным уравнением:

(1)

Числа Фибоначчи ,..., приведены в нижеследующей табл. 1.

Таблица 1

											...
											...

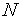Общее выражение для -го числа Фибоначчи можно получить из решения уравнения (1):

При больших значениях 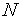членом (- )^N+1 можно пренебречь. При этом

(2)

Отсюда следует, что . Т.е. отношение двух соседних чисел Фибоначчи примерно постоянно и равно .

Алгоритм Фибоначчи.

Алгоритм Фибоначчи относится к классу поисковых методов оптимизации и включает в себя два этапа.

Первый этап состоит из ( 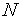-1)-й итерации для 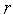=1,2,… 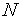-1. Рассмотрим схему 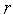-й итерации, когда ТИН_r=[ , ]:

1. Вычисляем величины

2. Вычисляем значения 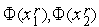функции ( ).

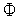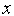3. Если 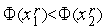, то выполняем присваивания 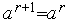, , 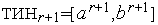. Иначе - выполняем присваивания , ,

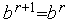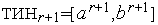
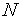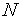Алгоритм Фибоначчи обладает тем свойством, что после выполнения ( -1)-й итерации имеет место следующая ситуация: . Т.е. в результате ( -1)-й итерации сужение текущего интервала неопределенности не происходит:

Второй этап призван решить, по какую сторону от точки лежит точка минимума функции ( ).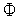

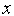Второй этап выполняется по следующей схеме:

1. Находим точку = + , где |ТИН_N-1| - свободный параметр алгоритма.

2. Вычисляем значение функции .

3. Если , то выполняем присваивания . Иначе - выполняем присваивания

В качестве приближенного значения точки минимума с равными основаниями может быть принята любая точка ТИН_N.