Функцияның монотонды болуының белгілері

Теорема. Егер u v функциялары өздерінің бірінші ретті туындыларымен бірге 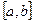аралығында үзіліссіз болса, онда мына формула орындалады:

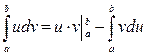бөліктеп интегралдау

Теорема. 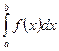бар болсын және 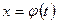функциясы мына шарттарды қанағаттандырсын:

1) 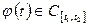2)

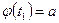
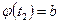
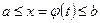
3) 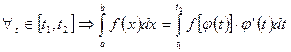айнымалыны ауыстыру.

Мысалдар. Алдымен бөліктеп интегралдауға келтіреміз.

1.

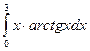
Шешуі:

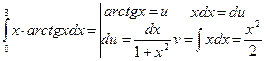
формулаға қоямыз:

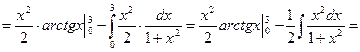
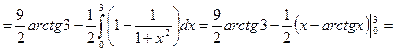
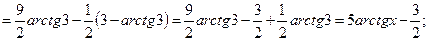
2.

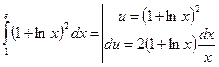
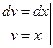
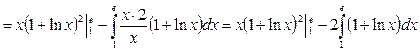
тағы да бөліктеп интегралдаймыз:

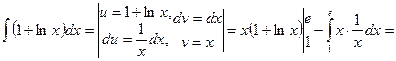
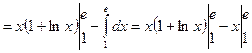орнына қоямыз.

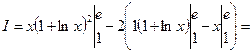
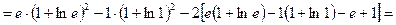
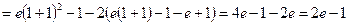
3.

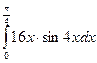
Шешуі: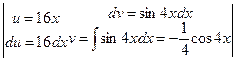

формулаға қойсақ:

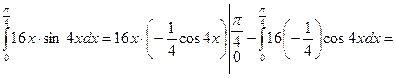
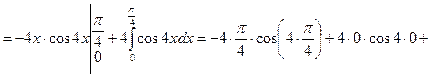
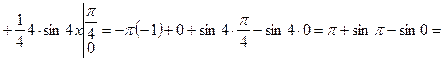
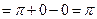
4. Келесі мысалдар айнымалыны ауыстыруға келтіріледі

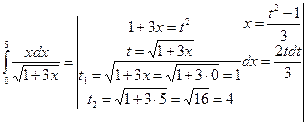
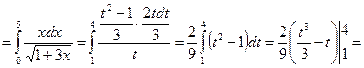
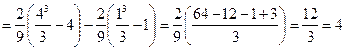
5.

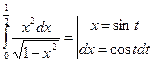
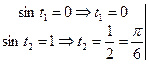
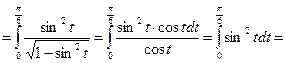
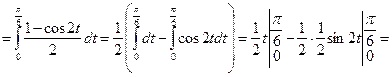
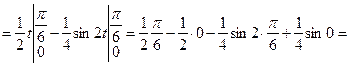
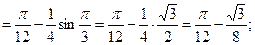
6.

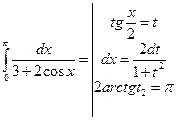
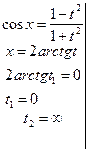
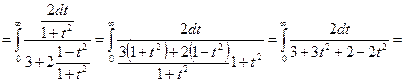
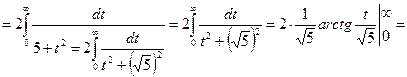
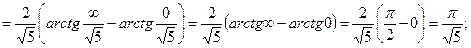
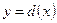функциясы 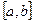кесіндісінде үздіксіз болсын. 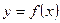функциясы белгілі болғандықтан 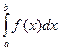интегралының мәні осы кесіндінің шеткі нүктелері а және bсандарына тәуелді болады.

Ал енді интегралдың төменгі шегі а-ны бекітіп қойып, жоғарғы шегі b-ны айнымалы деп қарасақ, онда интегралдың мәні осы жоғарғы шектің функциясы болады. Міне осыған ерекше көңіл аудару үшін анықталған интегралды мына

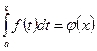түрде жазайық.

Бұл функцияның өте бір тамаша қасиеті бар. Оны теорема түрінде келтіріп дәлелдейік,

Теорема. Айнымалы жоғарғы шегі бойынша анықталған интегралдан алынған туындының мәні оның (интегралдың) астындағы функцияның интегралдың жоғарғы шегіндегі мәніне тең, яғни

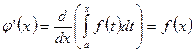
Дәлелдеуі: 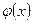функциясының туындысын табу үшін аргумент х-ке 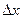өсімшесін береміз. Сонда

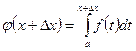және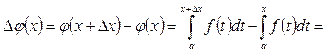

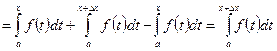
Осы теңдікке орта мән туралы теореманы, яғни қасиетті қолдансақ

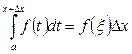мұндағы 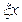және 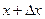аралығында: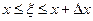

(немесе 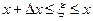, егер 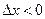).Сонымен,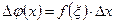

Бұдан 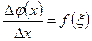осы жерде 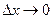ұмтылғандағы шекке көшсек

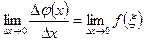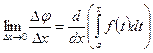Бірақ және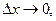

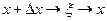
Ендеше,

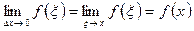Сонымен,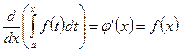

Орытынды

Елдің ертеңі білімнің тереңдігі мен өлшенеді демекші.Үздіксіз өзгеріп тұрған әлем адамнан да қабілет пен қажеттіліктерді үздіксіз дамытуды талап етеді.Сондықтан білім беру саласының басты мақсаты оқушыларды өзгермелі өмірде қорықпай, еркін өмір сүруге, білім мен білігіне сай келетін бағдар таңдап алатындай дәрежеге, өз бетінше жұмыс істеу дағдыларын қалыптастыруға, аналитикалық ойлау қабілеттерін дамыту және олардың шынайы өмірде дара тұлға етіп қалыптасуына ықпал ету.

«Шәкірт – нығырлай беретін ыдыс емес, керісінше тұтандыруды талап ететін шырақ» демекші оқушылардың жеке шығармашылық мүмкіндіктерін дамыту және оларды шынайы өмірдегі дара тұлға етіп дайындау мектептің басты мақсаттарының бірі.

Қорыта айтқанда,математика пәнінің қиын тақырыптарының бірі тізбектің шегі тақырыбы аясында тізбектің мәні,мүшелері,қасиеттері қорытылып,тәсілдері анықталып,теоремалар дәлелденді. Оқушының пәнге қызығушылығын дамыта түсу мақсатына бағытталған тапсырмалар қамтылды., Таңдау компоненті ретінде бұл тақырыпты талқылау университетімізде оқытылып келе жатқан болашақ математика мұғалімдері үшін берері көп екені анық.