Задачи геофизической интерпретации

Процедуры геофизической интерпретации, как указывалось выше, включают в себя обработку данных и реконструкцию физической модели в рамках зафиксированных моделей среды, модели поля и модели связи между ними. Реализуются эти этапы посредством специализированных процедур решения обратных задач, о которых речь пойдет ниже. Однако, такое расчленение этапов не всегда явно обнаруживается, прослеживается. Грани между ними оказываются размытыми в ситуациях, когда от геофизических данных требуют формирование лишь самых общих представлений об изучаемой среде и самых предварительных выводов об особенностях ее строения. Они начинают четче прорисовываться при повышении требований к результативности геофизической интерпретации и в полном объеме прослеживаются и играют ключевую роль при детальном анализе, имеющим целью максимально полное извлечение физико-геологической информации из комплекса геолого-геофизических данных. В этой связи остановимся на характеристики содержательных задач, решаемых в процессе геофизической интерпретации. Таких задач выделяется три. Это задачи обнаружения и локализации аномальных объектов. Построение их изображений и построение содержательных моделей среды. Рассмотрим подробней перечисленные задачи.

1.4.1. Обнаружение и локализация аномальных объектов – исторически первая задача, возникшая в практике геофизических работ. Под аномальными объектами понимаются объекты или участки изучаемой среды, отличающиеся по своим свойствам от окружающей среды так, что это отличие проявляется в регистрируемых физических полях и (или) наблюдаемых. Сама эта задача состоит в собственно выделении и обнаружении факта наличия аномального объекта и его локализации – т.е. оценке пространственного расположения и принятия решения о значениях общих параметров, характеризующих объект – глубины залегания, размерах, возможно формы. С целью решения первой из указанных задач необходимо максимально подчеркнуть – выделить компоненты наблюдаемой, характерные для аномального объекта, и затушевать, стереть все остальное, отнеся это к шумам, регулярным и нерегулярным помехам

Рис.1.6 Классификация задач геофизической интерпретации.

Для этой достижения этой цели необходимо применить процедуры обработки над наблюдаемыми, которые в рамках принятых предположений о свойствах полезного сигнала - собственно изучаемой аномалии и его отличиях от всего остального обеспечивают наиболее рельефное его выделение. Например, максимизируют отношение сигнал/помеха, хотя это и не является обязательным. Надежное принятие решения о наличии аномального объекта не обязательно должно основываться на критерии максимума отношения сигнал/помеха. Более эффективными могут оказаться критерии косвенных оценок, основанные на взаимных влияниях параметров и корреляции многих факторов. Принятие решений о характере объекта сопровождаемой оценкой его параметров – вторая из подзадач, характерная для локализации обнаруженного аномального объекта. При ее решении используется достаточно грубая аппроксимационная, содержательная модель среды. В качестве примера можно привести задачи гравиметрии, в которых этот этап состоит, например, в уподоблении реального объекта некоторому телу правильной геометрической формы – цилиндру, шару, уступу, пирамиде и последующему расчету параметров этого идеализированного объекта по «очищенной» предварительными процедурами обработки гравитационной аномалии. Также и в сейсморазведке вычисляются параметры плоской отражающей границы раздела по предварительно выделенному процедурами обработки в волновом поле годографу.

1.4.2. Построение изображенийэто особый класс задач геофизической интерпретации. На протяжении всего периода развития интерпретационного обеспечения геофизических методов параллельно развивались два подхода к извлечению информации из геофизических данных. Их весьма условно можно подразделить на геофизическую интроскопию и геофизическую интрометрию.

Понятие геофизической интрометрии объединяет методы преобразования геофизических данных, позволяющие определить численные значения содержательных физических параметров, характеризующих физическую модель геологического объекта. Соответственно используется аппроксимационная содержательная физико-геологическая модель, например, плотности, скорости распространения упругих волн и так далее. К геофизической интрометрии относятся методы решения обратных задач, рассматриваемые далее, позволяющие реконструировать значения параметров выбранной модели. Они позволяют найти характерные для выбранной модели и максимально близко соответствующие наблюдаемым геофизическим данным значения физических параметров. Однако эффективность такого рода методов в ряде случаев ограничена необходимостью знания требуемой содержательной параметризации, обеспечивающую единственность восстановления значений параметров, т.е. решения обратной задачи. Ошибки в выборе параметризации, а по сути рабочей геологической гипотезы, ведут к их усугублению на этапе решения обратных задач – об этом говорилось выше. В подобных ситуациях желательно «увидеть» объект, даже если параметры, в которых реализуется это видение, несодержательны и допускают произвол в толковании. Это необходимо для формирования последующих геологических гипотез и введения содержательных моделей и их параметризаций. Таковы задачи изучения локальных неоднородностей внутри изучаемых объектов, например, зон дробления в условиях солянокупольной тектоники или терригенных образований в рифовых структурах. Сюда относятся и изучение нетрадиционных ловушек нефти и газа – тектонически и литологически экранированных залежей. Эти подходы реализуются в методах геофизической интроскопии, которые объединяют методы преобразования геофизических полей, направленных на построение изображений изучаемых сред – реконструкцию их эффективных моделей. Отличие от принципов геофизической интрометрии состоит в том, что физический смысл параметра, в терминах которого строится изображение геологической среды, может быть неопределен либо носить условный, эффективный характер. В современных условиях, характеризующихся изучением сложнопостроенных сред, введение эффективных моделей среды для построения их изображений сред с целью последующего уточнения геологических гипотез и формирования содержательных моделей стало настоятельной необходимостью. Этот этап является предварительным для построения уточненных моделей и целесообразен при решении всего спектра задач геофизической интерпретации. Однако не следует и переоценивать его результативность для последующей реконструкции содержательной физико-геологической модели и геологической интерпретации. Это именно обеспечивающий промежуточный интерпретационный прием.

1.4.3. Построение содержательных моделей– это наиболее важная цель геофизической интерпрета­ции. В зависимости от меры дробности используемой аппроксимационной модели изменяется ее аппроксимационная способность (см. 1.3.1). Желание улучшить, ближе к действительности реконструировать физическую модель среды ведет к использованию моделей с улучшенными аппроксимационными способностям для описания широкого класса объектов 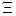. При движении в этом направлении на определенном этапе n используемая аппроксимационная модель оказывается столь широкой, что по заданному физическому полю нельзя однозначно реконструировать элемент из . Это явление называется эквивалентностью, и оно состоит как в том, что на как существуют тождественные по физическому полю элементы, так и возникают более тонкие эффекты скрытой эквивалентности. Эффекты скрытой эквивалентностипри повышении дробности аппроксимационных конструкций проявляются еще до того, как возникли эффекты эквивалентностии состоят в том, что найденный при реконструкции элемент, будучи единственным в заданном модельном классе (i<n) на самом деле приближенно описывает не ту реальность, под которую строился класс , а некоторую ему эквивалентную по физическому полю, но не имеющую содержательного смысла. Для того чтобы пояснить сказанное, приведем некоторые формальные выкладки.

Пусть оператор, отображающий элементы пространства (например, распределения плотности) в элементы пространства 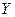(например, гравитационные поля). Собственно это оператор, суть некоторое уравнение математической физики, реализующее связь между физической моделью среды, элементы которой и физическим полем, обозначаемым 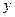. Пусть - модельный класс, который с точностью позволяет аппроксимировать элементом реальное распределение плотности (для его аппроксимации и строился класс ). Это означает, что:

.

Предполагается что класс, обладающий относительно оператора свойством единственности: если то из следует .

Если - заданное физическое поле и то задача реконструкции на состоит, например, в следующем:

Таково содержание аппроксимационного подхода в поиске физической модели на выделенном модельном классе. В результате ее решения будет получен элемент , служащий аппроксимацией на классе эквивалентности элемента:

Эффект скрытой эквивалентности состоит в возможном несовпадении, а в практически значимых, поддающихся анализу случаях фатально принципиальных различиях между .

Задачи расчленениясостоят в реконструкции среды с использованием аппроксимационных моделей, позволяющих разделить объект на составные части – элементарные тела. Число этих искомых элементарных составных частей должно быть таким, чтобы выделить все основные черты модели среды, но при этом избежать появления эффектов скрытой и, тем более, явной эквивалентности. Чаще всего, это задачи описания изучаемого объекта набором небольшого числа элементарных геометрических объектов. Задача, таким образом, состоит в нахождении составляющих, из которых сложен изучаемый объект, при не слишком высоком числе этих составляющих. Как правило, сюда не входят задачи изучения некоторых внутренних локальных неоднородностей и тем более задач нахождения распределения параметров внутри объекта.

Задачи детального описаниянаоборот, направлены на изучение моделей сред, заведомо находящихся за чертой эквивалентности и, тем более чертой скрытой эквивалентности. Типичным примером такой задачи служит изучение зон локальных неоднородностей, построение распределение физического параметра внутри изучаемого объекта. При этом речь идет не о построении серии формальных эквивалентных моделей, а о тщательном анализе, направленном на выделении из теоретически эквивалентных моделей наиболее приближенной к реальности. Из такого определения задач, а точнее их основного свойства вытекает, что решаться они могут только с использованием всего комплекса дополнительных к геофизическому полю данных. Можно выделить два подхода к такому комплексному использованию данных для реконструкции по физическому полю содержательной модели, соответствующей ее детальному описанию. Первая это пассивная формаиспользования комплекса дополнительных к физическому полю данных. Она соответствует ситуации, когда реконструируется содержательная модель среды по одному физическому полю, а все дополнительные данные об изучаемой модели используются в проинтерпретированной относительно изучаемых параметров модели форме. Эти данные, представляющие систему ограничений, условий, критериев выбора можно свести к единой форме – критерию оптимальности, определяющему систему предпочтений, принципов отбора «правильного» решения из теоретически допустимого множества эквивалентных. Такой подход называется интегрированной интерпретацией. Его результатом служит одна содержательная модель, оптимальным образом учитывающая весь комплекс дополнительных данных. Эти интегрированные дополнительные данные отнесены к параметрам изучаемой модели и именно поэтому подход называется интегрированной интерпретацией. Другой подход составляет содержание активной формы использования комплекса данных. Его суть состоит в том, что предполагается наличие не одного, а нескольких (например, двух) физических полей, каждому из которых следует сопоставить свою содержательную модель. Что же касается всех дополнительных данных, то они делятся на два класса. К первому относятся персонализированные данные о каждой из изучаемых моделей отдельно. Ко второму относится информация о взаимосвязи между параметрами самих реконструируемых моделей. Например, такой информацией может служить требование, состоящее в том, что для «правильных моделей» их должным образом нормированные аналоги менее всего друг от друга уклоняются в определенном, заранее заданном смысле. Например, для «правильных моделей» достигается максимум корреляционного отношения или минимум нормы взаимного уклонения их нормированных аналогов. Нормирование здесь нужно для того, чтобы учесть различия в единицах измерения параметров. Результатом такого подхода служит система содержательных моделей, каждая из которых с заданной точностью соответствует своему физическому полю, а в своей совокупности они образуют оптимальный комплекс относительно введенных критериев взаимосвязи и данных о каждой из модели. Такой подход, приводящий к построению системы, комплекса моделей, называетсякомплекснойинтерпретаций.

1.4.4. Эволюционно – динамический анализ– одна из наиболее сложных, многокомпонентных и нерешенных задач геофизической интерпретации.

Построение геофизических моделей геологических сред должно быть согласовано с законами и принципами механики сплошных сред. Во-первых, речь идет о механической устойчивости предполагаемых конструкций на масштабах времен, равных времени образования этих конструкций. Требование механической устойчивости означает также и баланс всех сил, действующих на каждый из элементов среды. Принцип построения сбалансированных моделей относится и ко всем геофизическим полям. Второе обстоятельство связано со следующим. Каждая структура и каждое образование имеют свой генезис – свое происхождение. В формировании структуры принимало участие множество сил как внешних – тектонические движения структур более высокого порядка, катастрофические события, так и внутренних, диктуемых законами механики сплошных сред - взаимодействие элементов структуры между собой и окружающими образованиями, что, впрочем, входит составной частью в законы механики сплошных сред. Картину геологического строения можно считать завершенной только тогда, когда помимо согласования со всеми наблюдаемыми физическими полями, она количественно проанализирована с механико-реологических позиций, является непротиворечивой, устойчивой на своих геологических масштабах времени, выяснен ее количественный генезис – породившая ее динамика сил и соответствующая ей динамика перемещений. Процесс построения моделей геологической среды, таким образом, рассматривается как эволюция динамической системы, а найденная модель – как продукт этой эволюции. Исследования подобного рода составляют содержание эволюционно - динамического анализа геолого-геофизических данных.

К одной из частных задач эволюционно-динамического анализа относится также задача изучения движений поверхности Земли в результате действия длительных нагрузок и изменения физико-механических свойств горных пород, произошедшее, например, в результате деятельности человека: добыча нефти, газа и т.д. Математические модели этих задач основаны на законах механики сплошных сред и, чаще всего предназначены для того, чтобы произвести оценку возможных последствий длительной техногенной нагрузки в виде проседания, оползней, техногенных землетрясений.

Литература.

1. Ампилов Ю.П. Сейсмическая интерпретация. Опыт и проблемы. Москва, «Геоинформарк», 204, 277 с.].