Сопротивление при медленном движении шара в вязкой жидкости

При медленном (при малых числах Рейнольдса) стационарном движении сферы в вязкой жидкости величина силы сопротивления 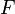зависит от вязкости жидкости 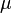, а также от скорости 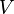и радиуса 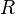сферы (плотность жидкости не входит в число определяющих параметров, так как при малых скоростях влияние инерции жидкости пренебрежимо мало). Применяя к зависимости

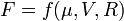пи-теорему, получаем

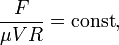
т.е. в этой задаче сила сопротивления находится с точностью до константы. Значение константы из соображений размерности не находится (решение соответствующей гидродинамической задачи даёт для константы значение 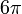, которое подтверждается экспериментально).

1. Что подразумевается под функциями Бесселя? – функции Бесселя в математике это семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: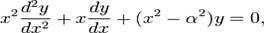

2. Физический смысл критерия Пекле? - критерий подобия, который характеризует соотношение между конвективным и молекулярным процессами переноса теплоты (вещества) в потоке жидкости, а также является критерием подобия для процессов конвективного теплообмена.

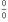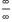3. Что представляет собой правило Лопиталя? - правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность типа или . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

4. Что такое невязка? - это ошибка (погрешность) в результате вычислений. Пусть мы хотим найти такое x, что значение функции: 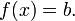. Подставляя приближенное значение x0 вместо x, получаем невязку 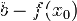, а ошибка в этом случае равна . Если мы не знаем точного значения x, мы не можем вычислить ошибку, но мы можем вычислить невязку.

Сплошна́я среда́ — механическая система, обладающая бесконечным числом внутренних степеней свободы. Её движение в пространстве, в отличие от других механических систем, описывается не координатами и скоростями отдельных частиц, а скалярным полем плотности и векторным полем скоростей. В зависимости от задач, к этим полям могут добавляться поля других физических величин (концентрация, температура, поляризованность и др.)

Однородная среда - среда, характеризующаяся равенством рассматриваемых физических свойств в любой точке пространства.

при M. т. происходит чрезвычайно сложное взаимодействие фаз, сопровождающееся различными физ.-хим. процессами, изменяющими состав, газодв-намич. и термодинамич. параметры каждой из фаз, их массовую долю и размеры включений (жидких либо твёрдых частиц, пузырьков). При взаимодействии фаз происходит обмен массой, импульсом и энергией. При M. т. процессы диффузии, вязкого взаимодействия, турбулентности, распространения звука, излучения, ударные волны существенно иные, чем при течении гомогенных смесей.

При матем. описании многофазной сплошной среды используют законы сохранения массы, импульса и энергии для каждой из фаз и смеси в целом, записанные в интегральной или дифференц. формах, применяя при этом понятие о многоскоростном континууме с взаимопроникающим движением составляющих. Многоскоростной континуум представляет собой совокупность N континуумов, каждый из к-рых относится к своей составляющей смеси и заполняет один и тот же объём, занятый смесью. Для каждого из этих составляющих континуумов в каждом потоке определяются плотность, скорость, а также и др. параметры. Тогда в каждой точке объёма, занятого смесью, будет определено N плотностей, темп-р и скоростей. Так, при течении газа с жидкими или твёрдыми частицами группы частиц разл. размеров с разными физ. свойствами образуют многоскоростной континуум в соответствии с числом таких групп.

Закон сохранения массы является частным случаем общего закона природы - закона сохранения энергии, который утверждает, что энергия изолированной системы постоянна. Энергия - это мера движения и взаимодействия различных видов материи. При любых процессах в изолированной системе энергия не производится и не уничтожается, она может только переходить из одной формы в другую.

Одной из форм энергии является так называемая энергия покоя, которая связана с массой соотношением Эйнштейна

Е₀ = m₀•с²,

СОХРАНЕНИЯ ЭНЕРГИИ ЗАКОН: в изолир. системе энергия системы остается постоянной, возможны лишь переходы одного вида энергии в другой. В термодинамике сохранения энергии закону соответствует первое начало термодинамики, к-рое выражается ур-нием Q = U + W, где Q-кол-во сообщенной системе теплоты, U-изменение внутр. энергии системы, W - совершенная системой работа. Частный случай сохранения энергии закона-Гесса закон.

Более общий закон сохранения массы и энергии: в изо-лир. системе сумма масс и энергии постоянна и возможны лишь превращения в строго эквивалентных соотношениях одних форм энергии в другие и эквивалентно связанные друг с другом изменения массы и энергии.

Ft=mv-mv_o=p-p_o=p.

Векторную величину Ft, равную произведению силы на время ее действия, называют импульсом силы. Векторную величину р=mv, равную произведению массы тела на его скорость, называют импульсом тела.

Число, или критерий Фурье (Fo) — один из критериев подобия нестационарных тепловых процессов. Характеризует соотношение между скоростью изменения тепловых условий в окружающей среде и скоростью перестройки поля температуры внутри рассматриваемой системы (тела), который зависит от размеров тела и коэффициента его температуропроводности:

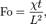
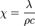· — коэффициент температуропроводности,

· t — характерное время изменения внешних условий,

· L — характерный размер тела.

Число Фурье является критерием гомохронности тепловых процессов, то есть связывает времена различных эффектов.

Число или критерий Пекле (Pe) — критерий подобия, который характеризует соотношение между конвективным и молекулярным процессами переноса тепла (примесей, количества движения, характеристик турбулентности) в потоке жидкости (соотношение конвекции и диффузии), а также является критерием подобия для процессов конвективного теплообмена.

Названо по имени французского физика Ж. К. Пекле (fr) (фр. J. С. Péclet, 1793—1857).

Используется при построении расчётных схем (метод конечных разностей, метод конечных элементов) для решения дифференциальных уравнений в частных производных, описывающих течения вязкой жидкости.

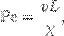
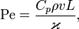где

L — характерный линейный размер поверхности теплообмена;

μ— скорость потока жидкости относительно поверхности теплообмена;

χ — коэффициент температуропроводности;

Cp— теплоёмкость при постоянном давлении;

ρ — плотность жидкости;

Ϟ — коэффициент теплопроводности жидкости.

При малых значениях Pe преобладает молекулярная теплопроводность, а при больших — конвективный перенос теплоты.

Число Пекле связано соотношением 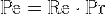с числом Рейнольдса и числом Прандтля.

Число Прандтля (Pr) — один из критериев подобия тепловых процессов в жидкостях и газах, учитывает влияние физических свойств теплоносителя на теплоотдачу:

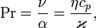где

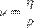— кинематическая вязкость;η — динамическая вязкость;p — плотность;Ϟ — коэффициент теплопроводности;

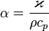— коэффициент температуропроводности;

Cp — удельная теплоёмкость среды при постоянном давлении.

Названо в честь немецкого физика Людвига Прандтля, изучавшего вопросы тепло- и массообмена в пограничных слоях.

Число Прандтля связано с другими критериями подобия — числом Пекле и числом Рейнольдса соотношением .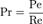

Число Струхаля (Sr, также Sh или St) — безразмерная величина, один из критериев подобия нестационарных течений жидкостей и газов, характеризующий постоянство протекания процессов во времени. Одна из формул, описывающих число Струхаля:

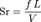, — частота вихреобразования; — характеристическая длина (например, гидравлический диаметр);

· — скорость потока.

Число Струхаля является функцией числа Рейнольдса Re, и в диапазоне 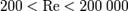действует эмпирический закон постоянства числа Струхаля: .

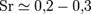Число или критерий Рейно́льдса ( 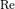) — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье-Стокса^[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Число Рейнольдса определяется следующим соотношением:

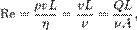
· ρ — плотность среды, кг/м³;

· v — характерная скорость, м/с;

· L — характерный размер, м;

· η — динамическая вязкость среды, Н*с/м²;

· ν — кинематическая вязкость среды, м²/с( ) ;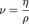

· Q — объёмная скорость потока;

· A — площадь сечения трубы.

Для каждого вида течения существует критическое число Рейнольдса, Re_cr, которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При Re < Re_cr течение происходит в ламинарном режиме, при Re > Re_cr возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения воды в круглой трубе .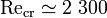

Число́ Фру́да (Fr) — один из критериев подобия движения жидкостей и газов, является безразмерной величиной. Применяется в случаях, когда существенно воздействие внешних сил. Введено Уильямом Фрудом в 1870 году.

Число Фруда характеризует соотношение между силой инерции и внешней силой, в поле которой происходит движение, действующими на элементарный объём жидкости или газа:

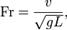
где v — характерный масштаб скорости, g — ускорение, характеризующее действие внешней силы , L — характерный размер области, в которой рассматривается течение.

Число Нуссельта (Nu) — один из основных критериев подобия тепловых процессов, характеризующий соотношение между интенсивностью теплообмена за счёт конвекции и интенсивностью теплообмена за счёт теплопроводности (в условиях неподвижной среды). Названо в честь немецкого инженера Вильгельма Нуссельта.

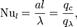^[1]

где:

· l — характерный размер;

· λ — коэффициент теплопроводности среды;

· a — коэффициент теплоотдачи;

· q_c — тепловой поток за счёт конвекции;

· q_λ — тепловой поток за счёт теплопроводности.

Число Шервуда (Sh) — критерий подобия для массообмена, равный отношению конвективного переноса к диффузии. Оно выражается следующим образом:

,

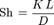где

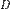· — коэффициент диффузии;

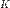· — коэффициент массообмена;

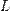· — характеристическая длина.

Диссипация энергии — переход части энергии упорядоченных процессов (кинетической энергии движущегося тела, энергии электрического тока и т. д.) в энергию неупорядоченных процессов, в конечном итоге — в тепло.

Конве́кция (от лат. convectio — принесение, доставка) — явление переноса теплоты в жидкостях или газах путем перемешивания самого вещества (как вынужденно, так и самопроизвольно). Существует т. н. естественная конвекция, которая возникает в веществе самопроизвольно при его неравномерном нагревании в поле тяготения. При такой конвекции нижние слои вещества нагреваются, становятся легче и всплывают, а верхние слои, наоборот, остывают, становятся тяжелее и опускаются вниз, после чего процесс повторяется снова и снова. При некоторых условиях процесс перемешивания самоорганизуется в структуру отдельных вихрей и получается более или менее правильная решётка из конвекционных ячеек.

Различают ламинарную и турбулентную конвекцию.

Градиент (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, показывающий направление наискорейшего возрастания некоторой величины 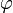, значение которой меняется от одной точки пространства к другой (скалярного поля).

Часто тензор представляют как многомерную таблицу 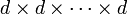(где d — размерность векторного пространства, над которым задан тензор, а число сомножителей совпадает с «валентностью тензора»), заполненную числами (компонентами тензора).

Коэффициент диффузии отражает скорость диффузии и определяется свойствами среды и типом диффундирующих частиц. Зависимость коэффициента диффузии от температуры выражается следующим уравнением: D = D₀exp( − E_a / kT), где D — коэффициент диффузии [ {м²}/{сек} ]; E_a — энергия активации [Дж]; k — постоянная Больцмана; T — температура [⁰K]