Метод LU-факторизации

В методе LU-факторизации (эту схему называют компактной схемой Гаусса) при решении системы 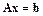выполняется следующая последовательность действий.

Матрица 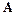представляется в виде произведения

,

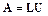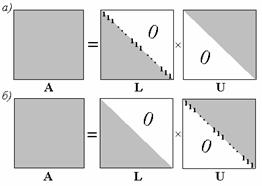
Рис. 2.3. Структура матриц L и U в разложениях Дулиттла (а) и Краута (б)

где L- нижняя треугольная матрица, U- верхняя треугольная матрица. Такое разложение единственно при условии предварительного выбора диагональных элементов одной из матриц. В этом случае число элементов в матрице A совпадает с суммарным числом неизвестных элементов матриц L и U. Если диагональ L принимается единичной, то такое разложение называют разложением Дулиттла (рис. 2.3,а), если единична диагональ U – разложением Краута (рис. 2.3,б). В дальнейшем при построении метода LU-факторизации будем привлекать разложение Краута.

Система 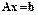заменяется системой

,

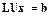легко решаемой за два шага:

Шаг 1. 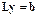. Принимая во внимание треугольный вид матрицы L, нетрудно получить, что в алгоритме Краута

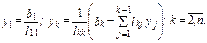
Шаг 2. 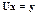. Решение этой системы в алгоритме Краута:

.

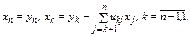Суммарные затраты реализации обоих шагов при n>>1 составляют 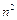длинных операций.

Получим соотношения для расчета элементов матриц L и U в алгоритме Краута. Для этого перемножим матрицы L и U и приравняем результат к A. По правилу перемножения матриц

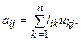
Учтем, что

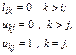
Рассмотрим элемент 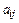(рис. 2.4), расположенный на центральной диагонали либо в нижней треугольной части матрицы A. Для такого элементаi ≥ j. Из рисунка следует, что

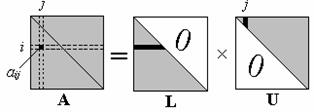
Рис. 2.4. Иллюстрация вычисления элемента матрицы, расположенного

ниже главной диагонали

,

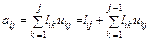так как i ≥ j и 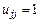. Отсюда

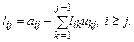
Рассмотрим элемент 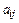(рис. 2.5), находящийся выше главной

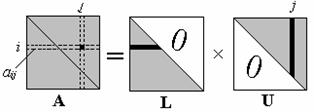
Рис. 2.5. Иллюстрация вычисления элемента матрицы, расположенного

выше главной диагонали

диагонали матрицы A(для него j>i). В этом случае

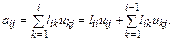
Следовательно,

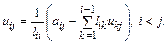
Получили в итоге соотношения, которые позволяют вычислять элементы матриц Lи U. Последовательность вычислений: сначала вычисляется столбец матрицы L, далее строка матрицы U, затем опять столбец матрицы L, далее строка матрицы U и т. д. (см. рис. 2.6, который иллюстрирует последовательность вычислений и схему хранения матриц L и U).

Вычисление столбца матрицы Lи строки матрицы Uназовем шагом LU-разложения. Приведем в качестве примера схему хранения элементов матриц A,L,U после второго шага LU-разложения (рис. 2.7).

Число длинных арифметических операций на этапе LU-разложения при n>>1 составляет величину 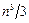, на шаге решения ли-

нейных систем с треугольными матрицами – 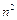. Суммарное число длинных операций приближенно равно 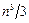(как и в методе Гаусса),

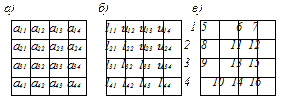
Рис. 2.6. Исходная матрица A (а), схема хранения L и U матриц (б), последовательность вычисления элементов в принятой схеме хранения (в)

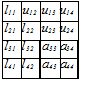
Рис. 2.7 Схема хранения элементов 4´4 матриц A, L, U после второго шага LU-факторизации

т. е. основные затраты приходятся на LU-факторизацию матрицы A. Эта особенность делает особо привлекательным метод LU-факторизации при решении СЛАУ с одной и той же матрицей A, но разными правыми частями:

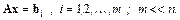
В этом случае факторизация матрицы выполняется однократно, требуя 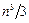длинных операций, а решение каждой системы с соответствующей правой частью реализуется за 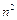таких операций.

Метод Холесского.

Исключительно эффективную реализацию метода LU-факторизации можно получить, если ограничиться классом линейных систем с симметрической положительно определенной матрицей A, т. е. 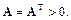Такую реализацию называют методом Холесского, либо методом квадратного корня.

Будем полагать, что решаемая система

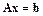
имеет симметрическую положительно определенную матрицу A. В этом случае матрица A представляется в виде

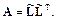
Здесь 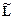– нижняя треугольная матрица. Такое разложение существует и единственно для положительно определенных симметрических матриц.

Система преобразуется к виду

.

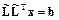Вектор 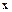ищется путем последовательного решения двух систем с треугольными матрицами:

; .

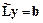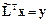Для получения расчетных соотношений элементов матрицы 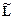рассмотрим произвольный элемент матрицы A:

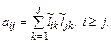
Суммирование здесь выполняется только до j, т. к. j≤i. Выделим член при значении k=j:

.

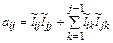Теперь

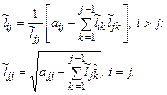
Эти соотношения позволяют вычислить по столбцам элементы матрицы .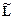

Эффективность такого метода достигается на этапе разложения матрицы, т. к. необходимо вычислить в этом случае только матрицу 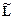. Арифметические затраты в методе Холесского составляют 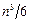длинных операций и n операций извлечения квадратного корня.

Существует другой вариант разложения симметрической положительно определенной матрицы, в котором удается избежать операций извлечения квадратного корня. В этом варианте вводится новая матрица 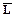по правилу

,

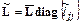причем 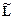– матрица, вычисленная ранее по схеме Холесского, 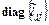– диагональная матрица с элементами 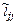матрицы 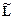. Матрица 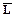существует и является нижней треугольной с единичной диагональю. В этом случае

,

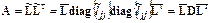где

.

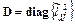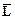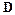Расчетные соотношения для элементов матриц и можно получить, как и прежде, привлекая правило перемножения матриц

,

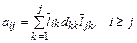из которого следует, что

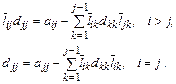
т. к. матрица 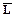имеет единичную диагональ.

Такой алгоритм потребует вдвое большего числа перемножений, чем схема Холесского. Однако, если ввести замену переменных

,

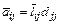то расчетные соотношения примут вид

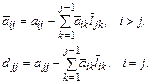
Здесь сначала вычисляют вспомогательные величины 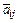, а затем их используют для определения искомых величин 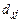и 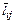. Количество умножений при такой организации алгоритма составляет приблизительно 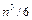и не содержит операции извлечения квадратного корня.

Лекция 3