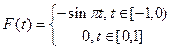Интеграл Фурье для четной и нечетной функции

Пусть f(x)-четная функция, удовлетворяющая условиям представимости интегралом Фурье.

Учитывая, что

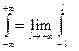, (6.4.1)

а также свойство интегралов по симметричному относительно точки x=0 интервалу от четных функций, из равенства (6.4.1) получаем:

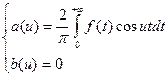(6.4.2)

Таким образом, интеграл Фурье четной функции f(x) запишется так:

,

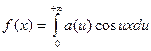где a(u) определяется равенством (6.4.2).

Рассуждая аналогично, получим, для нечетной функции f(x) :

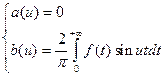(6.4.3)

и, следовательно, интеграл Фурье нечетной функции имеет вид:

,

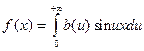где b(u) определяется равенством (6.4.3).

Комплексная форма интеграла Фурье

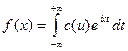, (6.4.4)

где

.

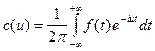Выражение в форме (6.4.4) является комплексной формой интеграла Фурье для функции f(x).

Если в формуле (6.4.4) заменить c(u) его выражением, то получим:

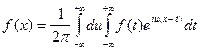, где правая часть формулы называется двойным интегралом Фуpье в комплексной форме. Переход от интеграла Фурье в комплексной форме к интегралу в действительной форме и обратно осуществим с помощью формул:

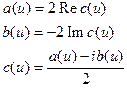
Формулы дискретного преобразования Фурье

Обратное преобразование Фурье:

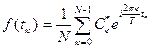
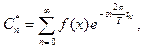где n=1,2,... , k=1,2,...

Дискретным преобразованием Фурье - называется N-мерный вектор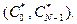

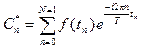
при этом, .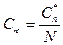

Раздел 7. Представление функции интегралом Фурье

Тема 7.1. Проверка условий представимости

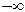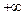Данную ранее функцию (6.4.2) доопределим на всей прямой от до как равную нулю (рис.7.1.1).

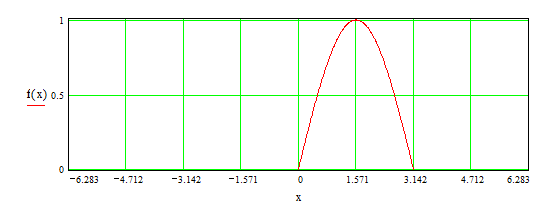
Рис.7.1.1

а) f(x)-определенна на R;

б) f(x) возрастает на ;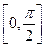

в) f(x) убывает на 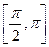- кусочнo-монотонна;

г) f(x) = const на 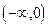и .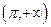

< .

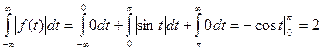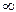Представление функции интегралом Фурье

В соответствии с теорией найдем a(u) и b(u):

;

.

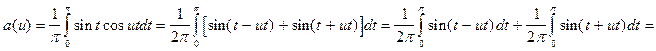
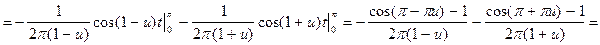
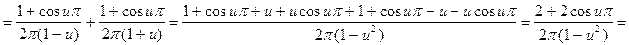
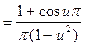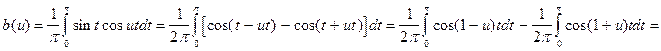
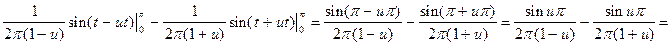
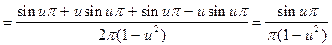И в конечном варианте интеграл Фурье будет выглядеть так:

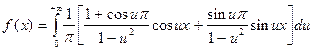
Интеграл Фурье в комплексной форме

Теперь представим интеграл Фурье в комплексной форме. На основе выше полученных разложений имеем:

,

,

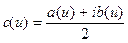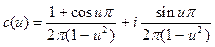а теперь получим интеграл в комплексной форме:

.

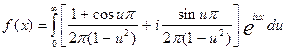Тема 7.2. Представление функции полиномом Лежандра

Основные сведения

Функцию можно разложить в ортонормированной системе пространства X=[-1,1] , причем полиномы получим, если проинтегрируем выражение:

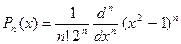
Соответственно получим для n=0,1,2,3,4,5, ... :

. . . . . . . . . .

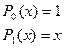
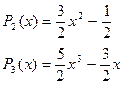
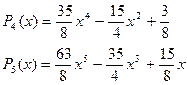
Для представления функции полиномом Лежандра необходимо разложить ее в ряд:

,

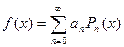где 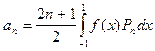и разлагаемая функция должна быть представлена на отрезке от -1 до 1.

Преобразование функции

Наша первоначальная функция f(x) имеет вид (см. рис.7.1), а т. к. она расположена на промежутке от 0 до 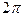необходимо произвести замену, которая поместит функцию на промежуток от -1 до 1.

Замена:

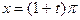
и тогда F(t) примет вид

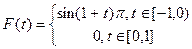
или