Задачи для подготовки к экзамену. Задания Построить корреляционное поле при помощи Мастера диаграмм(тип – Точечная диаграмма) и провести визуальный анализ

Задания

1. Построить корреляционное поле при помощи Мастера диаграмм(тип – Точечная диаграмма) и провести визуальный анализ.
2. Сформировать расчетную таблицу заданной структуры.

№	X	Y	XY	X^2	Y^2	Y_предск	E	E^2	(Y-Y_сред)^2	(Y_предск-Y_сред)^2	Abs(E/Y)
Сумма
Среднее

1. Ввести ряды данных в таблицу по столбцам. Рассчитать суммы и средние рядов данных с помощью функций СУММ(…) и СРЗНАЧ(…).
2. Рассчитать параметры линейного выборочного уравнения парной регрессии 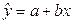с использованием формул:

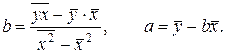
1. Найти значения выборочных дисперсий и СКО X, Y по формулам:

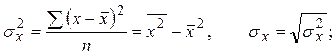
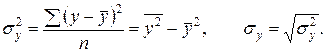
Проверить с помощью функцийДИСПР(…) иСТАНДОТКЛОНП(…).

1. Рассчитать выборочный коэффициент корреляции с использованием одной из формул:

.

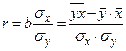Проверяем с помощью функции КОРРЕЛ(…).

1. Вычислить средний коэффициент эластичности .
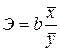2. Вычислить предсказанные моделью значения Y по построенному уравнению регрессии .
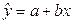3. Вычислить остатки и их квадраты. Остатки вычисляются по формуле
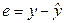
4. Вычислить значения (Y-Y_сред)^2, (Y_предск-Y_сред)^2.
5. Рассчитать суммы квадратов отклонений (СумКО), дисперсии и СКО на 1 степень свободы (общая, факторная, остаточная).

, , ,

, , ,

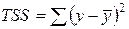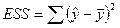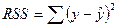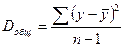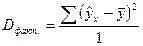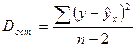где TSS – общая СумКО (total sum of squares), ESS – регрессионная СумКО (regression sum of squares), RSS – остаточная СумКО (residual sum of squares).

1. Проверить балансовое соотношение для суммы квадратов отклонений:

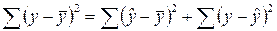
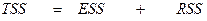
1. Рассчитать коэффициент детерминации 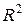и индекс корреляции с 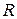использование сумм квадратов отклонений:

, .

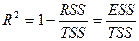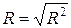Проверить с использованием коэффициента корреляции 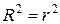и с помощью функции
КВПИРСОН(…).

1. Рассчитать стандартную ошибку коэффициента регрессии и значение статистики Стьюдента:

.

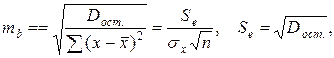
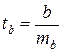1. Проверить статистическую значимость коэффициента b на уровнях 0,05 и 0,01. При определении табличного значения статистики воспользоваться функцией СТЬЮДРАСПОБР(…). Если |t_b|>t_табл(α;n-2), то коэффициент b статистически значимо отличен от нуля.
2. Построить доверительный интервал для коэффициента регрессии на уровне значимости 0,01:

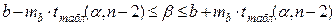
1. Рассчитать значение статистики Фишера F через факторную и остаточную дисперсии:
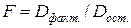
2. Проверить результат вычисления статистики с использованием коэффициента детерминации и статистики Стьюдента для b:

,

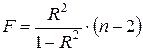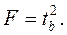
1. Проверить статистическую значимость уравнения в целом на уровне 0,05. Табличное значение F определить через функцию FРАСПОБР(…). Если 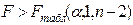, то уравнение статистически значимо в целом.

20. Проверить качество уравнения по средней относительной ошибки аппроксимации:

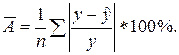
1. С помощью инструмента Регрессия Пакета анализа построить линейную регрессию объема продаж на время расходы на рекламу. Cпрогнозировать расходы на рекламу в 1 квартале следующего года 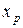, если среднее значение Х увеличить на 5 %.
2. Подставить прогноз расходов на рекламу в уравнение регрессии объема продаж и получить прогноз объема продаж в 1 квартале следующего года.
3. Построить 95% -й интервал прогноза объема продаж в 1 квартале следующего года:

,

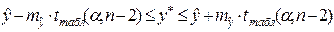a) среднего прогнозного значения:

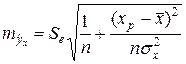
b) индивидуального прогнозного значения:

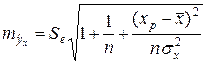
Задачи для подготовки к экзамену

Задача 1. Зависимость спроса на кухонные комбайны y от цены x по 20 торговым точкам компании имеет вид: 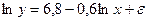, t_a=2,7; t_b=-2,8. Ранее предполагалось, что увеличение цены на 1 % приводит к уменьшению спроса на 1,2 %. Можно ли утверждать, что приведенное уравнение регрессии подтверждает это предположение?

Задача 2. Для двух видов продукции А, Б зависимость удельных постоянных расходов от объема выпускаемой продукции выглядит следующим образом

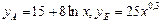Сравнить эластичности затрат по каждому виду продукции при x=50 и определить объем выпускаемой продукции обоих видов, при котором их эластичность будут одинаковы.

Задача 3. Пусть имеется уравнение парной регрессии: 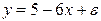, построенное по 15 наблюдениям. При этом r=-0.7. Определите доверительный интервал с вероятностью 0,99 для коэффициента регрессии в этой модели.

Задача 4. Уравнение регрессии потребления материалов в зависимости от объема производства, построенное по 15 наблюдениям, имеет вид: 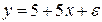,t_b=4. Определите коэффициент детерминации для этого уравнения.

Задача 5. Уравнение регрессии имеет вид : ln y = 4,5 + 0,003x + ln e. При значении фактора, равном 85, определите коэффициент эластичности Y по X.

Задача 6. По совокупности 15 предприятий торговли изучается зависимость между ценой 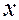на товар А и прибылью 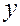торгового предприятия. При оценке линейной регрессионной модели были получены следующие результаты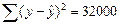 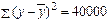Определите индекс корреляции, фактическое значение F- критерия, значимость уравнения регрессии.

Задача 7. Изучалась зависимость вида y=a*xb. Для преобразованных в логарифмах переменных (X, Y) получены следующие данные

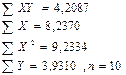
Определите значение параметра b.

Задача 8. Изучалась зависимость вида y=a+b*x+e. Получены следующие данные

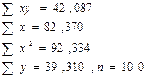
Определите значение параметра b.

Задача 9. Зависимость объема продаж Y от расходов на рекламу X характеризуется по 12 предприятиям концерна следующим образом

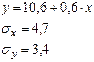
Определите t-статистику коэффициента регрессии.

Задача 10. По совокупности 15 предприятий торговли изучается зависимость между ценой 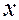на товар А и прибылью 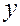торгового предприятия. При оценке квадратической регрессионной модели были получены следующие результаты: 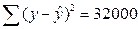, 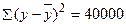. Определите фактическое значение F- критерия, значимость уравнения регрессии.